Le equazioni di secondo grado

Un'equazione di secondo grado è un'equazione in cui l'esponente più alto dell'incognita è pari a due. $$ ax^2 + bx + c = 0 $$

La forma generale dell'equazione di secondo grado è

$$ ax^2 + bx + c = 0 $$

La variabile x è l'incognita dell'equazione. In un'equazione di 2° grado il massimo esponente dell'incognita è 2.

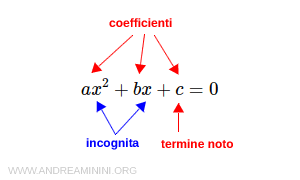
Le lettere a,b,c sono i coefficienti e possono avere segno positivo o negativo

• a = primo coefficiente
• b = secondo coefficiente
• c = terzo coefficiente

Il coefficiente c è anche detto termine noto.

Nota. Il coefficiente a deve essere sempre diverso da zero $$ a \ne 0 $$ Se il coefficiente a fosse nullo l'equazione sarebbe di primo grado. I coefficienti b e c, invece, possono anche essere uguali a zero. Ad esempio, se b=0 l'equazione di 2° grado diventa $$ ax^2 + c = 0 $$

Quando l'equazione di 2° grado ha il coefficiente a=1 è detta in forma normale

$$ x^2 + bx + c = 0 $$

Nota. Per ottenere la forma normale mi basta dividere l'equazione di 2° per il coefficiente a $$ \frac{ax^2 + bx + c}{a} = \frac{0}{a} $$ $$ \frac{ax^2}{a} + \frac{bx}{a} + \frac{c}{a} = 0 $$ $$ x^2 + \frac{b}{a}x + \frac{c}{a} = 0 $$

Se tutti i coefficienti a,b,c sono diversi da zero (a≠0 , b≠0, c≠0) l'equazione è detta equazione completa.

Viceversa, se uno o due dei coefficienti (b,c) sono nulli è detta equazione incompleta.

In particolar modo se l'equazione di 2° è incompleta è detta

• equazione spuria
  se il termine noto è nullo (c=0) e il secondo coefficiente è diverso da zero (b≠0) $$ x^2 + bx = 0 $$
• equazione pura
  se il termine noto è diverso da zero (c≠0) e il secondo coefficiente è nullo (b=0) $$ x^2 + c = 0 $$
• equazione monomia
  se il termine noto (c=0) e il secondo coefficiente (b=0) sono nulli $$ ax^2 = 0 $$

Le soluzioni dell'equazione di secondo grado

Risolvere un'equazione di 2° grado vuol dire trovare le soluzioni dell'equazione.

La soluzione dell'equazione di 2° grado è un valore che sostituito alla variabile incognita x rende vera l'uguaglianza tra il primo e il secondo membro dell'equazione. $$ ax^2 + bx + c = 0 $$

 

Le soluzioni dell'equazione di secondo grado sono anche dette radici

Una equazione di 2° ha al massimo due soluzioni. Può comunque averne anche una sola oppure non averne alcuna.

Esempio

Questa equazione di 2° grado

$$ 2x^2 -4x - 6 $$

posso risolverla sostituendo l'incognita con il valore x=3

$$ 2·(3)^2 -4·(3) - 6 = $$

$$ 2·9 -12 - 6 = $$

$$ 18 -18 = 0 $$

L'equazione ha anche un'altra soluzione. Si tratta di x=-1

$$ 2·(-1)^2 -4·(-1) - 6 = $$

$$ 2·1 + 4 - 6 = $$

$$ 2 - 2 = 0 $$

Non è sempre facile trovare a colpo d'occhio le soluzioni.

Fortunatamente, per trovare tutte le soluzioni di un'equazione di 2° esiste un metodo di calcolo numerico che rende la ricerca molto rapida e semplice.

 

Come trovare tutte le soluzioni di un'equazione di 2° grado

Per trovare le soluzioni di un'equazione di 2° grado basta applicare questa formula risolutiva$$ x = \frac{-b \pm \sqrt{b^2-4ac}}{2a} $$ Per vedere la dimostrazione della formula.

Il radicando è detto discriminante e si indica con la lettera greca delta maiuscola Δ.

$$ \Delta = b^2-4ac $$

Nota. Se il coefficiente b dell'equazione di 2° è un numero pari posso usare anche la formula ridotta di risoluzione $$ x = \frac{-\frac{b}{2} \pm \sqrt{(\frac{b}{2})^2-ac}}{a} $$ Si ottiene dividendo per 2 sia il numeratore che il denominatore. $$ x = \frac{-b \cdot \frac{1}{2} \pm \sqrt{b^2-4ac} \cdot \frac{1}{2} }{2a \cdot \frac{1}{2} } $$ $$ x= \frac{- \frac{b}{2} \pm \sqrt{(b^2-4ac)\cdot \frac{1}{4} } }{2} $$ $$ x= \frac{ - \frac{b}{2} \pm \sqrt{ \frac{b^2}{4}- \frac{4ac}{4} }}{a } $$ $$ x= \frac{ - \frac{b}{2} \pm \sqrt{ (\frac{b}{2})^2- ac }}{a } $$

Il segno del discriminante è fondamentale per capire se l'equazione di 2° ha soluzioni

• Se Δ>0 l'equazione di 2° ha due soluzioni distinte x₁ e x₂ nell'insieme dei numeri reali.
• Se Δ=0 l'equazione di 2° ha una sola soluzione x₁ nell'insieme dei numeri reali o per meglio dire due soluzioni reali coincidenti x₁ = x₂ (doppia soluzione).
• Se Δ<0 l'equazione di 2° non ha soluzioni nell'insieme dei numeri reali.

  Nota. Se il discriminante è minore di zero Δ<0 l'equazione ha comunque soluzioni nell'insieme dei numeri complessi (radici complesse e coniugate).

Dal punto di vista grafico l'equazione di secondo grado è una parabola che ha per asse di simmetria la retta verticale

$$ x = - \frac{b}{2a} $$

e per vertice della parabola il punto

$$ V \begin{pmatrix} \ - \frac{b}{2a} \ ; \ - \frac{b^2-4ac}{4a} \ \end{pmatrix} $$

Pertanto, le radici (soluzioni) sono i punti della parabola che intersecano l'asse delle ascisse (x).

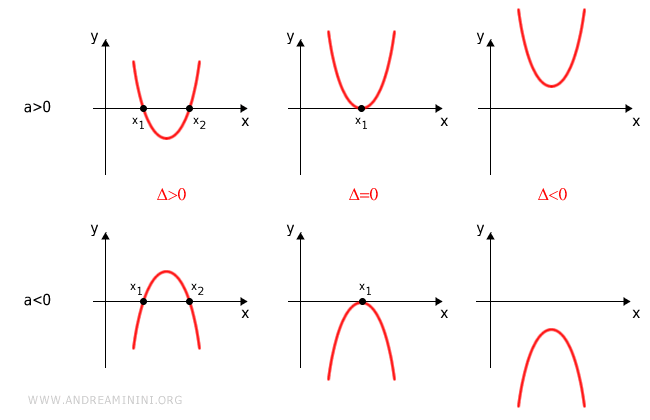
Le parabole sono rivolte verso l'alto o verso il basso a seconda se il coefficiente a è positivo (a>0) o negativo (a<0).

Un esempio pratico

Provo a risolvere questa equazione di 2°

$$ 2x^2 -4x - 6 $$

I coefficienti dell'equazione sono a=2, b=-4, c=-6

Uso la formula per trovare le soluzioni

$$ x = \frac{-b \pm \sqrt{b^2-4ac}}{2a} $$

$$ x = \frac{-(-4) \pm \sqrt{(-4)^2-4 \cdot 2 \cdot (-6)}}{2 \cdot 2} $$

$$ x = \frac{4 \pm \sqrt{(16+48)}}{4} $$

$$ x = \frac{4 \pm \sqrt{64}}{4} $$

Il discriminante (64) è positivo Δ>0 quindi l'equazione di 2° ha due soluzioni nell'insieme dei numeri reali.

La radice quadrata di 64 è ±8 perché 8·8=64 ma anche (-8)·(-8)=64.

$$ x = \frac{4 \pm 8}{4} $$

Semplifico

$$ x = \frac{1 \pm 2}{1} $$

$$ x = 1 \pm 2 $$

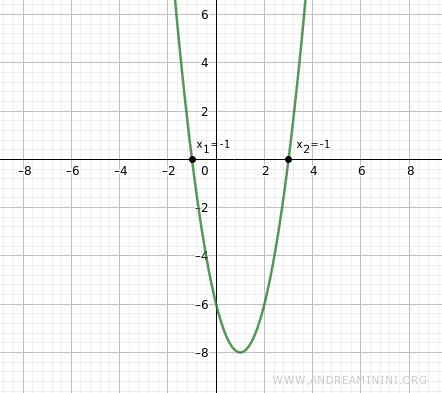
Quindi le radici (soluzioni) dell'equazione sono x₁=-1 e x₂=3.

$$ x = \begin{cases} 1 - 2 = -1 \\ \\ 1 + 2 = 3 \end{cases} $$

Dal punto di vista grafico l'equazione è una parabola rivolta verso l'alto perché il coefficiente a>0.

La dimostrazione

Per dimostrare la formula di risoluzione delle equazioni di 2° grado

$$ ax^2 + bx + c = 0 $$

Applico la proprietà invariantiva e moltiplico entrambi i membri per 4a

$$ 4a \cdot ( ax^2 + bx + c) = 4a \cdot 0 $$

$$ 4a^2x^2 + 4abx + 4ac = 0 $$

$$ 4a^2x^2 + 4abx = - 4ac $$

Applico di nuovo la proprietà invariantiva aggiungendo b²-b² al primo membro dell'equazione

$$ 4a^2x^2 + 4abx +b^2 - b^2 = - 4ac $$

$$ 4a^2x^2 + 4abx +b^2 = b^2- 4ac $$

Il primo membro dell'equazione è un quadrato (2ax+b)²

$$ (2ax+b)^2 = b^2- 4ac $$

Calcolo la radice quadrata a entrambi i membri dell'equazione

$$ \sqrt{ (2ax+b)^2 } = \sqrt{ b^2- 4ac } $$

$$ 2ax+b = \sqrt{ b^2- 4ac } $$

Esplicito la x e ottengo la formula che volevo dimostrare

$$ 2ax = - b \pm \sqrt{ b^2- 4ac } $$

$$ x = \frac{ - b \pm \sqrt{ b^2- 4ac } }{2a} $$

La regola della somma e del prodotto delle radici

Se già conosco una soluzione (radice) dell'equazione di 2° grado posso ricavare l'altra usando una delle due seguenti regole

• La regola della somma delle radici
  La somma delle radici è uguale al rapporto tra i coefficienti b e a cambiato di segno.
  $$ x_1 + x_2 = - \frac{b}{a} $$
• La regola del prodotto delle radici
  Il prodotto delle radici è uguale al rapporto tra i coefficienti c e a
  $$ x_1 \cdot x_2 = \frac{c}{a} $$

Queste regole mi permettono di calcolare la radice mancante usando i coefficienti a,b,c dell'equazione ax²+bx+c=0 senza dover risolvere l'equazione di 2°

 

Esempio. In un'equazione di 2° grado $$ x^2 +4x + 3 = 0 $$ Se conosco una radice x₁=-1 dell'equazione posso ricavare l'altra radice x₂ usando i coefficienti a=1 c=3 dell'equazione. $$ x_2 = \frac{c}{a \cdot x_1} = \frac{3}{1 \cdot (-1)} = -3 $$ Questa regola è particolarmente utile se una radice è banale e visibile a colpo d'occhio, oppure, per qualsiasi altra ragione è già nota.

Come scomporre un trinomio di 2° grado

Un trinomio di secondo grado con discriminante non negativo Δ≥0 posso scomporlo in un questa forma equivalente $$ ax^2 + bx + c = a \cdot (x-x_1) \cdot (x-x_2) $$ Dove x₁ e x₂ sono le soluzioni reali (dette zeri) dell'equazione.

Esempio

Riprendo l'equazione di 2° già risolta nell'esempio precedente

$$ 2x^2 -4x - 6 = 0 $$

Questa equazione ha due soluzioni reali x₁=-1 e x₂=3

Pertanto, posso ridurla nella forma equivalente a(x-x₁)(x-x₂) sapendo che a=2

$$ a \cdot (x- x_1) \cdot (x-x_2) = 0 $$

$$ 2 \cdot (x- (-1)) \cdot (x-3) = 0$$

$$ 2 \cdot (x+1) \cdot (x-3) = 0 $$

Verifica. Svolgo i calcoli algebrici a partire dalla forma equivalente. $$ 2 \cdot (x+1) \cdot (x-3) = 0 $$ $$ (2x+2) \cdot (x-3) = 0 $$ $$ 2x^2-6x +2x-6 = 0 $$ $$ 2x^2-4x-6 = 0 $$ Il risultato finale è l'equazione iniziale di 2° grado. L'equivalenza è confermata.

E così via.