Intersezione di una parabola e una retta

L'intersezione di una retta con una parabola avviene al massimo in due punti.

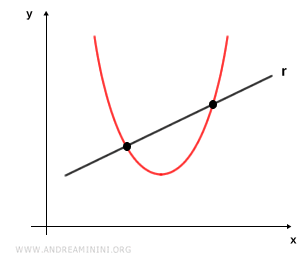
• Retta secante
  La retta è detta secante se interseca la parabola in due punti distinti.
  
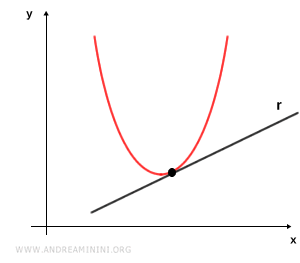
• Retta tangente
  La retta è detta tangente se interseca la parabola in un punto e non è parallela all'asse della parabola.
  
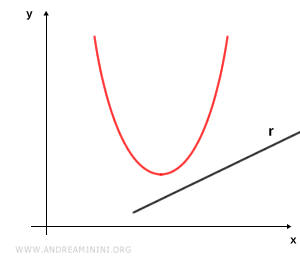
• Retta esterna
  La retta è detta esterna se non interseca la parabola.
  
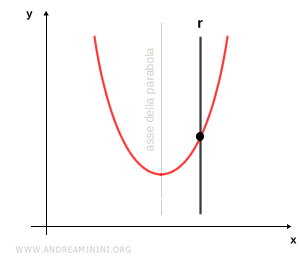
• Retta parallela all'asse della parabola
  Se la retta è parallela all'asse della parabola, anche in questo caso c'è un solo punto di intersezione ma la retta non è tangente alla parabola.
  

Come trovare i punti di intersezione tra la retta e la parabola

Per individuare i punti di intersezione tra una parabola e una retta non parallela all'asse della parabola, costruisco un sistema di equazioni di 2° grado.

$$ \begin{cases} y=ax^2+bx+c \\ \\ y = mx+q \end{cases} $$

La prima equazione di 2° grado è l'equazione della parabola.

La seconda equazione di 1° grado è l'equazione della retta.

Sapendo che y=a²+bx+c e y=mx+q posso eguagliare le due espressioni.

$$ ax^2+bx+c = mx+q $$

In questo modo ottengo un'equazione di 2° grado

$$ ax^2+bx-mx+c-q $$

$$ ax^2+x \cdot (b-m) + (c-q) $$

Chiamo a'=a, b'=b-m + c'=c-q

$$ a'x^2+x \cdot b' + c' $$

A questo punto calcolo il discriminante dell'equazione di 2° grado.

$$ \Delta = b'^2 - 4a'c' $$

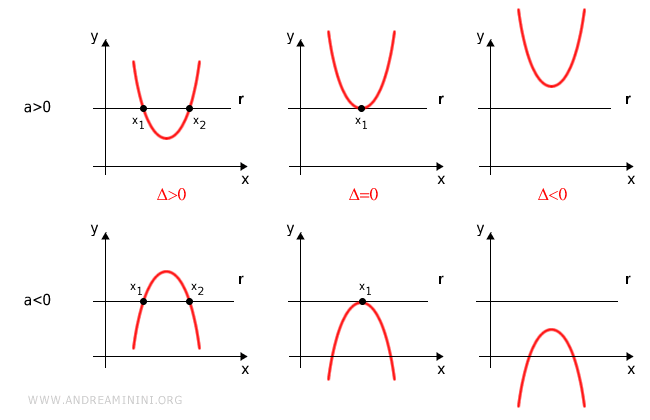
In base al discriminante ci sono tre ipotesi

• Δ>0
  Se il discriminante è positivo, la retta è secante alla parabola. Per trovare i punti di intersezione calcolo le due radici distinte dell'equazione di 2° grado.
• Δ=0
  Se il discriminante è positivo, la retta è tangente alla parabola. Per trovare il punti di tangenza calcolo le due radici coincidenti dell'equazione di 2° grado.
• Δ<0
  Se il discriminante è negativo, la retta è esterna alla parabola. Non ci sono punti di intersezione.

Un esempio pratico

Devo verificare se la retta

$$ y = -2x + 6 $$

è secante, tangente o esterna alla parabola

$$ y = - 2x^2+2x+4 $$

Eguaglio le due espressioni

$$ -2x + 6 = -2x^2+2x+4 $$

$$ 2x^2-2x-2x + 6-4 = 0 $$

$$ 2x^2-4x + 2 = 0 $$

Calcolo il discriminante dell'equazione di 2° grado

$$ \Delta =b^2-4ac = (-4)^2-4(2)(2) = 16 -16 = 0 $$

Il discriminante è Δ=0. Quindi, la retta è tangente alla parabola.

Per trovare il punto di tangenza trovo le radici dell'equazione di 2° grado

$$ x = \frac{-b \pm \sqrt{\Delta}}{2a} $$

$$ x = \frac{-(-4) \pm \sqrt{0}}{2(2)} $$

$$ x = \frac{4}{4} = 1 $$

Una volta trovato il punto x=1 calcolo il punto y usando l'equazione della retta o della parabola. L'una o l'altra è indifferente.

Utilizzo l'equazione della retta perché in genere mi permette di svolgere calcoli più semplici.

$$ y = -2x + 6 $$

Sapendo che x=1

$$ y = -2(1) + 6 $$

$$ y = 4 $$

Pertanto il punto di tangenza si trova alle coordinate x=1 e y=4 ossia nel punto (x;y)=(1;4).

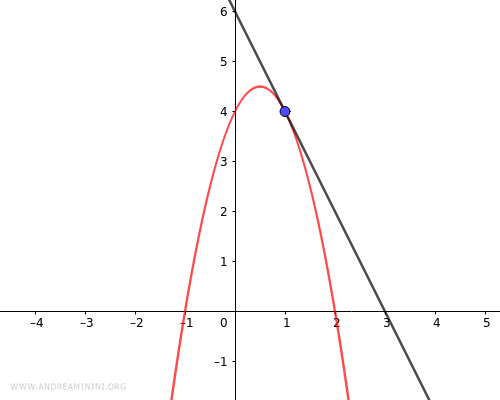
E così via.