Sistemi di disequazioni
Un sistema di disequazioni è un insieme composto da due o più disequazioni con la stessa variabile incognita (x). $$ \begin{cases} A(x) > B(x) \\ C(x) < D(x) \\ \vdots \\ W(x) \ge z(x) \end{cases} $$ Le soluzioni del sistema sono i valori reali dell'incognita che soddisfano contemporaneamente tutte le disequazioni.
Ecco un esempio pratico.
$$ \begin{cases} 2x + 1 < 3 \\ \\ 4x + 3 > 5 \end{cases} $$
Per risolvere un sistema di disequazioni devo trovare i valori delle incognite (x) che soddisfano contemporaneamente tutte le disequazioni del sistema.
Inizialmente risolvo ogni singola disequazione.
$$ \begin{cases} 2x + 1 - 1 < 3 - 1 \\ \\ 4x + 3 -3 > 5 -3 \end{cases} $$
$$ \begin{cases} 2x < 2 \\ \\ 4x > 2 \end{cases} $$
$$ \begin{cases} x < 1 \\ \\ x > \frac{1}{2} \end{cases} $$
Una volta trovate le soluzioni delle singole disequazioni, individuo gli intervalli in cui tutte le disequazioni sono soddisfatte.
$$ \frac{1}{2} < x < 1 $$
In questo modo ottengo le soluzioni comuni ossia le soluzioni del sistema di disequazioni.
Nota. Quando le disequazioni sono più di due, è molto utile ricorrere al metodo grafico per cercare le soluzioni comuni del sistema.
Come risolvere un sistema di disequazioni
Per risolvere un sistema di disequazioni
- Calcolo gli insiemi delle soluzioni delle singole disequazioni $$ S_1 \ , \ S_2 \ , \ \dots \ , \ S_n$$
- Le soluzioni del sistema sono i valori reali nell'intersezione degli insiemi $$ S = S_1 \cap S_2 ... \cap S_n $$
Nota. In pratica, rappresento su una retta orientata, detta quadro delle soluzioni, gli intervalli in cui le singole disequazioni sono soddisfatte. Poi individuo nel quadro delle soluzioni gli intervalli in cui tutte le disequazioni sono contemporaneamente soddisfatte ossia le soluzioni comuni.
Se il sistema di disequazioni non ammette soluzioni comuni in tutte le disequazioni, il sistema è detto impossibile.
Un esempio pratico
Esempio 1
In questo esercizio considero il sistema di disequazioni
$$ \begin{cases} 4x-8 \ge 0 \\ \frac{3x-12}{x+1} >0 \\ 2x-4< 6 \end{cases} $$
Costruisco il quadro delle soluzioni.
La prima disequazione 4x-8 ≥ 0 è soddisfatta quando x è maggiore o uguale a 2
$$ \begin{cases} x \ge \frac{8}{4} \\ \frac{3x-12}{x+1} >0 \\ 2x-4< 6 \end{cases} $$
$$ \begin{cases} x \ge 2 \\ \frac{3x-12}{x+1} >0 \\ 2x-4< 6 \end{cases} $$
Aggiungo la condizione x ≥ 2 nel quadro delle soluzioni del sistema.
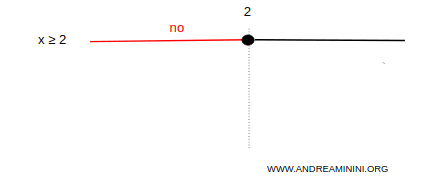
La seconda disequazione 3x-12/x+1 non è definita quando x=-1
Per trovare le soluzioni di questa disequazione devo studiare il segno del numeratore e del denominatore.
- La disequazione al numeratore 3x-12 > 0 è positiva per ogni x>12/3 ossia x>4
- La disequazione al denominatore x+1 > 0 è positiva per ogni x>-1
Applico la regola del segno per capire in quali intervalli la frazione 3x-12/x+1 > 0 è soddisfatta
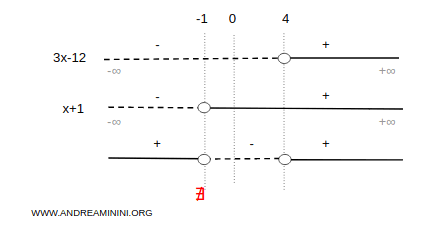
Pertanto la seconda disequazione è soddisfatta negli intervalli (-∞, -1) U ( 4, ∞)
Aggiungo questo intervallo al quadro delle soluzioni del sistema.
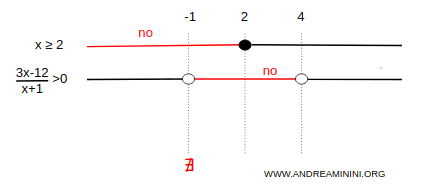
La terza disequazione 2x-4<6 è vera quando x<10/2 ossia x<5
$$ \begin{cases} x \ge 4 \\ \frac{3x-12}{x+1} >0 \\ x< \frac{6+4}{2} \end{cases} $$
$$ \begin{cases} x \ge 4 \\ \frac{3x-12}{x+1} >0 \\ x< 5 \end{cases} $$
Aggiungo la condizione x<5 al quadro delle soluzioni.
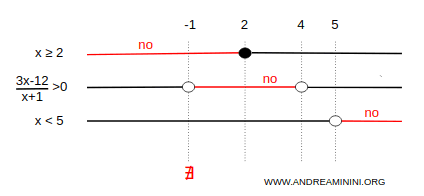
A questo punto posso trovare la soluzione del sistema.
Le disequazioni sono contemporaneamente soddisfatte nell'intervallo (4-5).
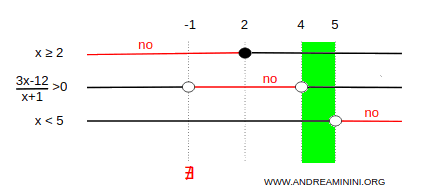
Pertanto, la soluzione del sistema di disequazioni è ogni valore reale dell'incognita x nell'intervallo (4-5).
$$ 4 < x < 5 $$
Esempio 2
Considero questo sistema di disequazioni
$$ \begin{cases} x - 4< 0 \\ 2-x > 0 \\ x+3>0 \end{cases} $$
Utilizzo i principi di equivalenza per trovare le soluzioni delle singole disequazioni.
$$ \begin{cases} x - 4+4< 0+4 \\ 2-x-2 > 0-2 \\ x+3-3>0-3 \end{cases} $$
$$ \begin{cases} x< 4 \\ -x > -2 \\ x>-3 \end{cases} $$
Moltiplico per -1 entrambi i membri della seconda disequazione, cambiando il verso della relazione d'ordine.
$$ \begin{cases} x< 4 \\ -x \cdot (-1) > -2 \cdot (-1) \\ x>-3 \end{cases} $$
$$ \begin{cases} x< 4 \\ x < 2 \\ x>-3 \end{cases} $$
Ho individuato le soluzioni di ogni singola disequazione.
A questo punto le rappresento graficamente. In questo modo è più facile trovare le soluzioni comuni.
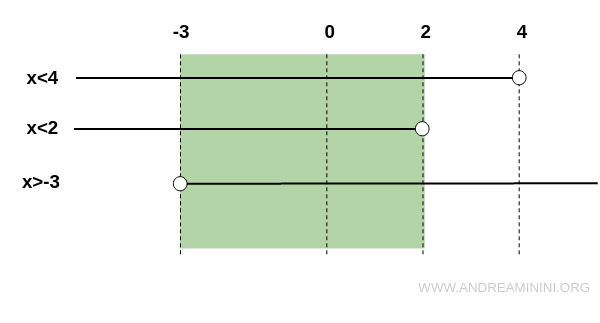
In questo caso l'intervallo delle soluzioni comuni a tutte le disequazione è
$$ -3 < x < 2 $$
Questa è la soluzione del sistema di disequazioni.
E così via.
