I sistemi di equazioni lineari a gradini
Un sistema di equazioni lineari è detto sistema a gradini o a scalini, se è possibile scriverlo in questa forma.
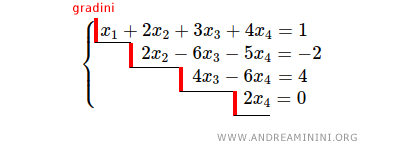
Il numero delle incognite in ogni equazione si riduce man mano che si passa dalla prima all'ultima equazione del sistema.
Il numero dei gradini del sistema lineare è uguale al rango.
In questo modo il calcolo del rango diventa molto semplice anche se il sistema è composto da numerose equazioni e variabili.
Perché i sistemi a gradini sono utili?
I sistemi lineari a gradini sono particolarmente facili da risolvere, perché posso trovare i valori delle incognite a partire dall'ultima equazione.
Se un sistema lineare non è a gradini, posso trasformarlo in un sistema a gradini usando il metodo di eliminazione di Gauss-Jordan.
Nota. Per essere un sistema a gradini ogni gradino deve scendere di una riga. Se la matrice scende di due o più righe non è una matrice a gradini.
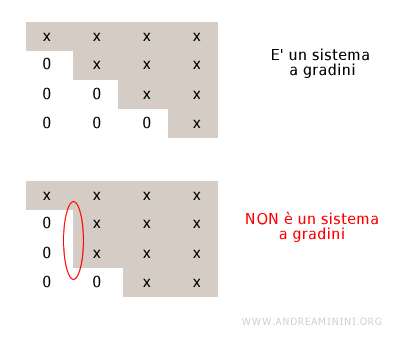
Se un gradino si estende su due variabili (colonne) una delle due variabili va trasformata in un parametro del sistema lineare.
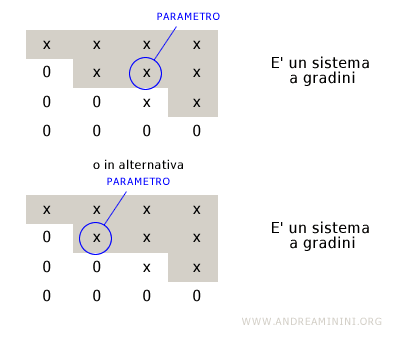
Un esempio pratico
Esempio 1
Questo sistema di equazioni lineari è a gradini
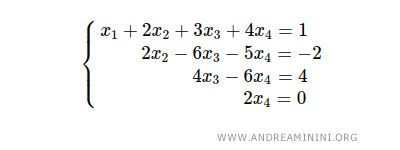
Il sistema ha 4 gradini e n=4 variabili incognite.

La matrice completa del sistema ha il rango uguale a r=4 perché il sistema ha 4 gradini.
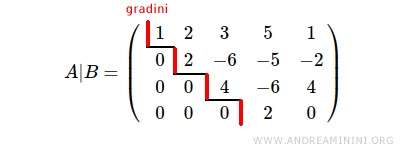
Anche la matrice dei coefficienti ha il rango uguale a 4 perché ci sono 4 gradini.
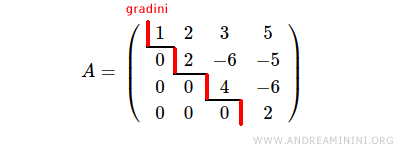
Pertanto, in base al Teorema di Rouché-Capelli il sistema ammette una o più soluzioni.
In questo caso ammette una soluzione perché il rango (r=4) è uguale al numero delle variabili (n=4).
$$ \infty^{n-r} = \infty^{4-4} = \infty^0 = 1 $$
Per risolverlo parto dall'ultima equazione 2x4=0 perché si risolve immediatamente. E' evidente che x4=0.
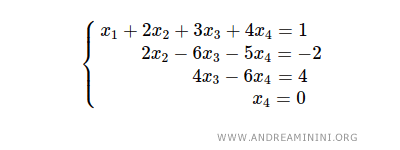
Sostituisco x4=0 nella terza equazione e ottengo 4x3=4 ossia x3=1 .
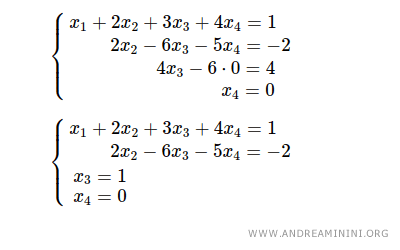
Sostituisco x3=1 e x4=0 nella seconda equazione e ottengo 2x2-6·1-5·0=-2 ossia x2=2 .
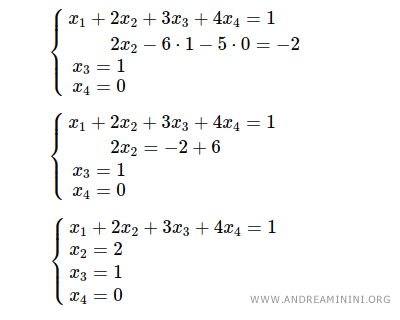
Infine, sostituisco x2=2 , x3=1 e x4=0 nella prima equazione e ottengo x1+2·2+3·1+4·0=1 ossia x1=-6 .
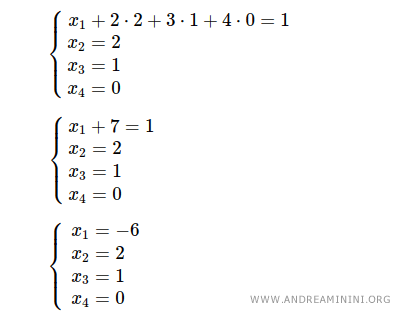
Ho risolto il sistema in pochi passaggi.
Le soluzioni del sistema sono x1=-6 , x2=2 , x3=1 e x4=0
Nota. Per questa ragione è molto utile trasformare un sistema di equazioni lineari in un sistema a gradini. La risoluzione del sistema diventa molto semplice anche se il sistema è composto da molte equazioni e variabili incognite.
Esempio 2
Anche questo sistema di equazioni lineari è a gradini
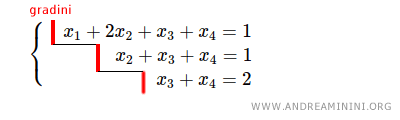
La matrice completa del sistema ha il rango uguale a r=3 perché il sistema ha 3 gradini.
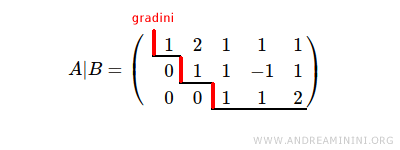
Anche la matrice dei coefficienti ha il rango uguale a r=3 per la stessa ragione.
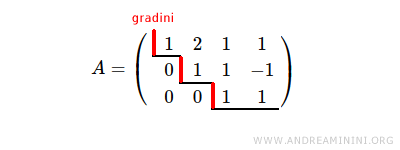
In base al Teorema di Rouché-Capelli il sistema ammette una o infinite soluzioni
In questo caso il sistema ammette infinite soluzione perché il rango (r=3) è inferiore al numero delle variabili (n=4)
$$ \infty^{n-r} = \infty^{4-3} = \infty^1 = \infty $$
Per trovare le soluzioni devo parametrizzare il sistema.
Ad esempio, nell'ultima equazione ricavo la variabile x3 usando la variabile x4 come parametro del sistema.
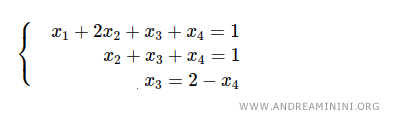
Poi sostituisco x3=2-x4 nella seconda equazione e trovo x2=-1.
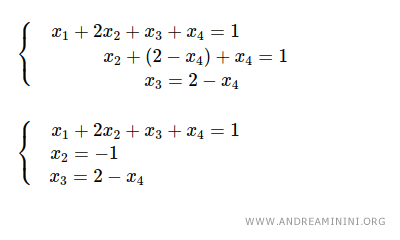
Infine, sostituisco x2=-1 e x3=2-x4 nella prima equazione e trovo x1=1.
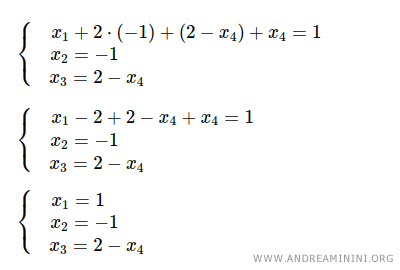
Le soluzioni del sistema di equazioni sono x1=1 , x2=-1 e x3=2-x4 considerando x4 come un parametro k=x4 con k∈R
$$ \begin{cases} x_1 = 1 \\ x_2 = -1 \\ x_3 = 2 - k \end{cases} $$
Pertanto, il sistema ha infinite soluzioni.
Osservazioni
Alcune osservazioni utili sui sistemi lineari a gradini
- Tutte le matrici a gradini sono matrici triangolari superiori. Non vale però l'inverso. Non tutte le matrici triangolari superiori sono anche matrici a gradini.
- Il determinante di una matrice a gradini quadrata è uguale il prodotto degli elementi sulla diagonale principale. Essendo una matrice triangolare il determinante si calcola semplicemente facendo il prodotto degli elementi sulla diagonale principale perché gli altri sono nulli. Per questa ragione il calcolo del determinante nelle matrici a gradini quadrate è molto semplice.
E così via.
