Numeri complessi

Cosa sono i numeri complessi

Un numero complesso z è una coppia ordinata di numeri reali (a,b) $$ z=(a,b) $$ che soddisfa le seguenti proprietà $$ (a,b) = (c,d) \: \text{se e solo se} \: a=c ∧ b=d $$ $$ (a,b)+(c,d)=(a+c,b+d) $$ $$ (a,b) \cdot (c,d) = (ac-bd,ad+bc) $$

Dove a e b sono numeri reali

• Il numero a è detto parte reale del numero complesso $$ Re(z) = a $$
• Il numero b è detto parte immaginaria del numero complesso. $$ Im(z)=b $$

Perché studiare i numeri complessi? Molti problemi non ammettono una soluzione con l'insieme dei numeri reali R. Ad esempio, la radice quadrata di -4 è impossibile perché non esiste un numero reale che elevato al quadrato sia uguale a un numero negativo.

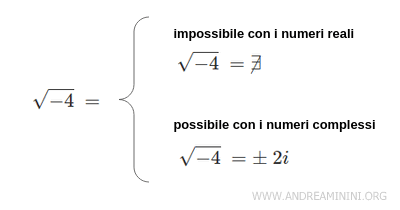
La radice di un numero negativo è invece risolvibile usando l'insieme dei numeri complessi C. In generale, l'insieme dei numeri complessi è molto più ampio dell'insieme dei numeri reali e mi permette di svolgere calcoli altrimenti impossibili con i numeri reali.

Ogni numero complesso è un elemento dell'insieme RxR perché è composto da una coppia ordinata (a,b) di numeri reali.

Quindi, posso considerare ogni numero complesso come un punto del piano cartesiano.

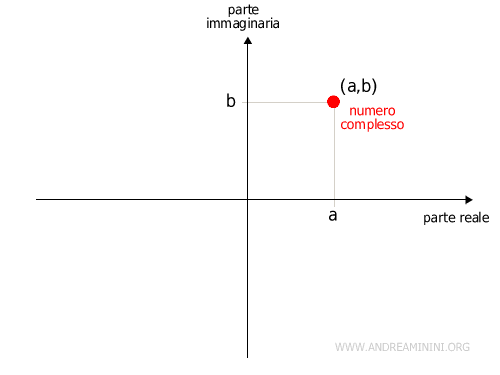
Per ogni punto del piano c'è un numero complesso e viceversa.

Nota. Non esiste un criterio generale per stabilire se un punto del piano è maggiore o minore di un altro. Posso solo dire se due punti sono uguali o diversi. Quindi, non posso dire se un numero complesso è maggiore o minore di un altro. Posso soltanto affermare che un numero complesso è uguale a un altro se i due numeri hanno la stessa parte reale e immaginaria.

La forma algebrica dei numeri complessi

Posso rappresentare un numero complesso anche in forma algebrica (o compatta) come la somma di un numero reale (a) e di un numero immaginario (i·b). $$ z = a + i \cdot b $$

Per spiegarlo parto dalla forma algebrica

$$ z = a+i·b $$

I termini a e b sono due numeri reali.

Essendo due numeri reali posso scriverli nella forma equivalente (a,0) e (b,0)

$$ z = (a,0) + i·(b,0) $$

Il termine i è l'unità immaginaria ed è pari a i=(0,1) mentre b è il coefficiente reale della parte immaginaria.

Sostituisco i=(0,1)

$$ z = (a,0) + (0,1)·(b,0) $$

Sapendo che il prodotto tra due numeri complessi si ottiene con la formula (x₁,y₁)(x₂,y₂)=(x₁x₂-y₁y₂, x₁y₂+x₂y₁)

$$ z = (a,0) + (0·b-1·0,0·0+1·b)$$

$$ z = (a,0) + (0-0,0+b)$$

$$ z = (a,0) + (0,b)$$

$$ z = (a+0,0+b) $$

$$ z = (a,b) $$

Il risultato finale è il numero complesso (a,b)

Cos'è un numero immaginario? Un numero immaginario è un multiplo dell'unità immagnaria i=(0,1). Quindi, è un numero complesso del tipo (0,a) con parte reale nulla. Ad esempio i·3 è il numero immaginario (0,3). In generale, i·k è un numero immaginario del tipo (0,k) dove k è il fattore moltiplicativo (o coefficiente della parte immaginaria) mente i è l'unità immaginaria. In questo modo posso percorrere il processo anche in verso contrario, partendo da un numero complesso (a,b) posso giungere alla forma algebrica a+bi. $$ (a,b) = (a,0) + (0,b) = (a,0) + (b,0) \cdot i = a + b \cdot i $$

L'insieme dei numeri complessi è indicato con la lettera C. E' un'estensione dell'insieme dei numeri reali.

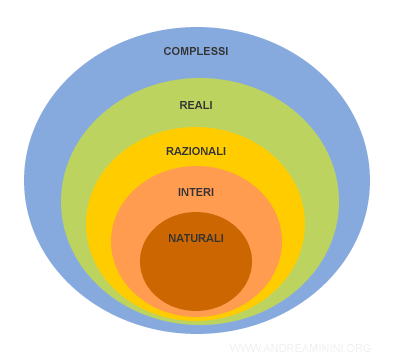
Sono particolarmente utili in fisica per studiare i fenomeni periodici e sinusoidali.

Un esempio pratico

Ho un numero complesso z

$$ z=2+3i $$

Posso riscrivere il numero sotto forma di coordinate cartesiane con x=2 e y=3

$$ (x,y)=(2,3) $$

$$ (x,y)=(2,0) + (0,3) $$

Nei numeri complessi posso ottenere (0,3) nel seguente modo

$$ (0,3) = (0,1)·(3,0) $$

Quindi sostituisco (0,3) con (0,1)·(3,0)

$$ (x,y)=(2,0) + (0,3) $$

$$ (x,y)=(2,0) + (0,1)·(3,0) $$

Sapendo che l'unità immaginaria i è uguale a (0,1)

$$ (x,y)=(2,0) + i·(3,0) $$

Le coppie con un elemento pari a zero indicano un numero reale.

Sostituisco (2,0)=2 e (3,0)=3 e ottengo il numero complesso nella sua forma algebrica.

$$ (x,y)=2 + i·3 $$

La rappresentazione del numero complesso sul piano cartesiano ( detto piano di Gauss o piano complesso ) è la seguente:

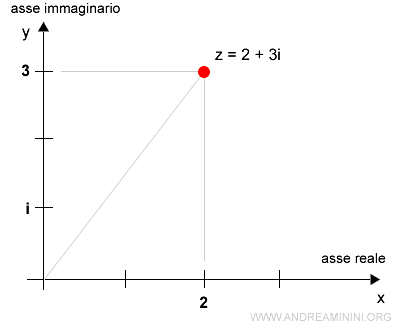
L'unità immaginaria, la parte reale e immaginaria

L'unità immaginaria dei numeri complessi è la coppia (0,1). Nella forma compatta/algebrica si indica con il simbolo i oppure j. $$ i=(0,1) $$

Le coppie di numeri con una coordinata nulla, pari a zero, identificano un numero reale.

$$ (a,0) = a $$

$$ (0,b) = b $$

Tra queste coppie è particolarmente utile la coppia (0,1) perché se moltiplicata per se stessa ha come risultato l'opposto -1

$$ (0,1)·(0,1) = (0·0-1·1,0·1+1·0) = (-1,0 ) = -1 $$

In questo modo è possibile risolvere le equazioni del tipo x²=-1.

Nota. L'unità immaginaria ha la particolarità $$ i^2 = (0,1)·(0,1) =-1 $$ Per questa ragione il prodotto di due numeri complessi è $$ z_1 · z_2 = (a+bi)(c+di)=ac+adi+bic+bd^2 =ac+adi+bic-bd = (ac-bd)+(ad+bc)i $$

Questa coppia è detta unità immaginaria (i) del numero complesso.

$$ (a,b) = (a,0)+(0,b) $$

Dove (0,b) può essere ottenuto con il prodotto complesso (0,1)·(b,0)

$$ (a,b) = (a,0)+(0,1)·(b,0) $$

Essendo (a,0) e (b,0) due numeri reali, posso riscrivere la forma compatta in questo modo

$$ z=a+i·b $$

Dove a è la parte reale del numero complesso mentre b è la parte immaginaria e i è l'unità immaginaria

A cosa servono i numeri complessi

I numeri complessi sono stati ideati per trovare delle soluzioni altrimenti impossibili nei numeri razionali.

Esempio 1

Questa equazione non ha soluzioni reali perché la radice quadrata non è definita nei numeri negativi.

$$ x^2 = -1 $$

Con i numeri complessi è invece possibile.

$$ x^2 = (-1,0) $$

Sapendo che (-1,0) nei numeri complessi si ottiene con il prodotto (0,1)·(0,1)

$$ (-1,0)=(0,1) \cdot (0,1) $$

Posso sostituire (-1,0) con (0,1)·(0,1)

$$ x^2 = (0,1)·(0,1) $$

Poiché la coppia (0,1) è l'unità immaginaria i.

$$ x^2 = i·i $$

$$ x^2 = i^2 $$

Mettendo tutto sotto radice ottengo il valore dell'incognita x

$$ \sqrt{x^2} = \sqrt{i^2} $$

$$ x = i $$

Posso riscrivere il numero complesso i nella forma algebrica

$$ x = 0 + i $$

Ho così trovato la soluzione del problema.

Esempio 2

Un'equazione di secondo grado nell'incognita z

$$ az^2 +bx + c = 0 $$

ammette due soluzioni reali se b²-4ac=>0

$$ \frac{-b ± \sqrt{b^2-4ac}}{2a} = \begin{cases} z_1 \\ z_2 \end{cases} $$

I coefficienti a,b,c dell'equazione sono in relazione con le soluzioni z₁ e z₂

$$ z_1+z_2 = - \frac{b}{a} $$

$$ z_1 \cdot z_2 = \frac{c}{a} $$

Questo però non vale per tutte le equazioni di secondo grado.

Ad esempio, l'equazione seguente non ha soluzioni nell'insieme dei numeri reali.

$$ z^2 + 1 = 0 $$

Nemmeno le relazioni tra i coefficienti possono essere soddisfatte

$$ z_1 + z_2 = 0 $$ $$ z_1 \cdot z_2 = 1 $$

Per fare in modo che tutte le equazioni di secondo grado abbiano una soluzione, devo passare dai numeri reali R ai numeri complessi C introducendo l'unità immaginaria z

$$ z = ± \sqrt{-1} $$

In questo modo ottengo algebricamente

$$ z^2 = -1 $$

E questo soddisfa sia l'equazione z²+1=0 che le relazioni tra i coefficienti.

La somma e il prodotto dei numeri complessi

Nell'insieme dei numeri complessi sono definite due operazioni:

• Somma
  La somma si svolge sommando gli elementi delle coppie con la stessa posizione $$ (a,b) + (c,d) = (a+c, b+d) $$

  Esempio. $$ (1,2) + (2,4) = (1+2, 2+4) = (3,6) $$

• Prodotto
  La formula del prodotto è meno intuitiva. Diventa però chiara una volta approfondito il significato dell'unità immaginaria. $$ (a,b) · (c,d) = (ac-bd, ad +bc ) $$

  Esempio. $$ (1,2) · (2,4) = (1·2-2·4, 1·4 +2·2 ) = (-6,8) $$

In entrambi i casi, il risultato finale è un altro numero complesso.

Nota. La sottrazione si svolge come l'addizione. $$ (a,b) - (c,d) = (a-c, b-d) $$ La divisione deve invece essere ricondotta alla moltiplicazione $$ \frac{a+bi}{c+di} = \frac{a+bi}{c+di} \cdot \frac{c-di}{c-di} = \frac{ac-adi+bic-bdi^2}{c^2-cdi+cdi -(di)^2} = \frac{ac-adi+bic-bd(-1)}{c^2- d^2(-1)} = \frac{(ac+bd)+ i (bc-ad)}{c^2+ d^2} $$ ossia $$ \frac{ac+bd}{c^2+ d^2} + i \cdot \frac{bc-ad}{c^2+ d^2} $$

Il confronto tra numeri complessi

Due numeri complessi sono uguali quando hanno la stessa parte reale e la stessa parte immaginaria.

Non è, invece, possibile definire una relazione d'ordine per confrontare due numeri complessi distinti.

In altre parole, non posso affermare che un numero complesso sia maggiore o minore di un altro, perché ogni numero complesso è composto da una coppia di numeri reali.

Esempio

Considero tre numeri complessi

$$ z_1 = 5+3i $$

$$ z_2 = 4+2i $$

$$ z_3 = 5+3i $$

Posso affermare che z₁ e z₃ sono uguali perché hanno la stessa parte reale (5) e immaginaria (3i).

Allo stesso modo posso dire che z₁ e z₂ sono diversi, ma non posso affermare che l'uno sia maggiore dell'altro.

Nota. Al massimo potrei confrontare i moduli dei numeri complessi per confrontare la loro distanza dall'origine. Tuttavia, non si tratta di un vero confronto dei numeri complessi, bensì della loro distanza dall'origine.

La forma cartesiana e la forma polare

Un numero complesso può essere rappresentato in due forme

• forma cartesiana
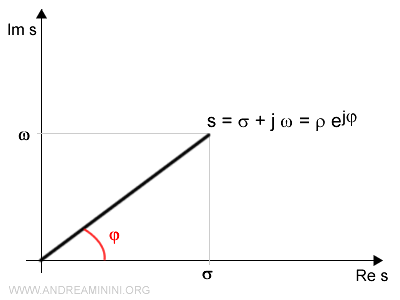
  $$ s=σ+jω $$
• forma trigonometrica
  $$ s=p(\cos φ + j \cdot \sin φ) $$
• forma polare ( o esponenziale )
  $$ s=p e^{jφ} $$

Dove σ è la parte reale, ω la parte immaginaria, p il modulo e φ l'argomento del numero complesso s.

Nota. L'argomento φ deve essere compreso tra -π e π ( pi greco ). $$ -π < φ ≤ π $$

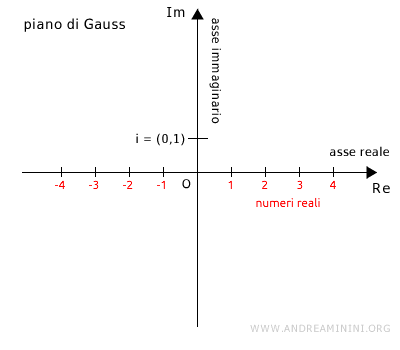
La rappresentazione dei numeri complessi

Posso rappresentare i numeri complessi su un piano cartesiano, detto piano di Gauss, con un asse reale e un asse immaginario.

E' detta rappresentazione dei numeri complessi in forma algebrica.

E' anche possibile rappresentare il numero nella forma trigonometrica o polare.

$$ z= p ( cos \: φ + j \cdot sin \: φ ) $$

Per passare dalla forma polare alla forma cartesiana

$$ σ = p \: \cos φ $$

$$ ω = p \sin φ $$

Valgono le seguenti relazioni $$ p = \sqrt{σ^2+ω^2} $$ $$ φ = \arctan \frac{ω}{σ} = \arcsin {ω}{\sqrt{σ^2+ω^2}} $$

Un'ulteriore rappresentazione è la forma esponenziale

$$ p \cdot e^{jφ} = p \cdot ( cos \: φ + j \cdot sin \: φ ) $$

Quest'ultima forma si basa sulla formula di Eulero

$$ e^{jφ} = cos \: φ + j \cdot sin \: φ $$

La funzione di variabile complessa

Una funzione di variabile complessa è una funzione definita nell'insieme dei numeri complessi. $$ f(z) $$ con $$ z=x+i \cdot y $$

Pertanto, una funzione di variabile complessa si può scrivere come

$$ w = f(s) = u(σ,ω)+i \cdot v(σ,ω) $$

dove u e v sono due variabili reali che rappresentano rispettivamente la parte reale e la parte immaginaria.

Esempio

La funzione reale e^iy può essere riscritta come funzione di variabile complessa, e viceversa.

$$ e^{iy} = \cos y + i \cdot \sin y $$

Dove i è l'unità immaginaria.

Lo stesso si può fare con il seno, il coseno, la radice quadrata, ecc.

Note

Alcune note  margine e osservazioni sui numeri complessi

• I numeri reali sono un sottoinsieme dei numeri complessi
  Un numero complesso con parte immaginaria nulla, come (a;0), è un numero reale ed è detto "numero reale complesso". Ogni numero di questo tipo ha un'associazione biunivoca con l'asse dell'ascisse nel piano complesso. Ad esempio, scrivere (2;0) oppure 2 identifica lo stesso punto dell'ascisse.
  
  Pertanto ogni numero reale appartiene anche all'insieme dei numeri complessi, ovvero l'insieme dei numeri reali è un sottoinsieme dei numeri complessi. $$ \mathbb{R} \subseteq \mathbb{C} $$ Le operazioni fra due numeri reali complessi danno gli stessi risultati delle operazioni tra due numeri reali. Questa proprietà si esprime dicendo che l'insieme dei numeri reali (R) è isomorfo al sottoinsieme C'⊆C dei numeri reali complessi formato dalle coppie (a;0) rispetto alle operazioni dell'addizione e della moltiplicazione.

  Esempio. Quando sommo due numeri complessi (2;0) e (3;0) ottengo (5;0). $$ (2;0)+(3;0)=(5;0) $$ E' lo stesso risultato che otterrei sommando i due numeri reali 2 e 3. $$ 2+3=5 $$ Allo stesso modo, il prodotto dei due numeri complessi è (6;0) $$ (2;0) \cdot (6;0) = (2 \cdot 3 - 0 \cdot 0 ; 2 \cdot 0 + 0 \cdot 6)= (6;0) $$ E' lo stesso risultato del prodotto tra i due numeri reali corrispondenti $$ 2 \cdot 3 = 6 $$

• Storia dei numeri complessi
  Raffaele Bombelli, nel XVI secolo, fu tra i primi a utilizzare esplicitamente i numeri immaginari. Indicava \(+i\) e \(-i\) rispettivamente come "più di meno" (p.d.m.) e "meno di meno" (m.d.m.) e li utilizzò per calcolare le radici quadrate di numeri negativi. Inizialmente i numeri immaginari erano considerati "quantità silvestri" o artifici matematici, erano utili ma non accettati pienamente come parte della matematica rigorosa. Cartesio coniò per primo il termine "numeri immaginari" per sottolineare l'apparente irrealtà. Nel Settecento, Gauss diede una rappresentazione geometrica ai numeri complessi e dimostrò il Teorema Fondamentale dell'Algebra, sancendo la rilevanza dei complessi nella matematica. Hamilton (1833) formalizzò i numeri complessi come coppie ordinate di numeri reali \((a, b)\), dove \(a + bi\) rappresenta ogni numero complesso. Successivamente, i numeri complessi furono applicati in molti campi del sapere (es. elettrotecnica). Questa evoluzione mostra come i numeri complessi siano passati da una concezione iniziale di strumenti "immaginari" a diventare un caposaldo della matematica e delle applicazioni tecnologiche.

E così via.