Equazioni differenziali

Cosa sono le equazioni differenziali?

Un'equazione differenziale è un'equazione in cui l'incognita è la funzione y=f(x) e i termini sono le derivate della funzione stessa. $$ F(x,y, y',...,y^{(k-1)}, y^{(n)} )=0 $$ Si tratta di una relazione tra una funzione y=f(x) e le sue derivate. Dove y è la funzione incognita, y⁽ⁿ⁾ sono le derivate della funzione incognita e x è la variabile indipendente.

Le funzioni in un'equazione differenziale devono essere continue e derivabili fino all'ordine n, ossia essere derivabili n volte (ordine o grado dell'equazione differenziale).

Nota. Quando una funzione è continua e derivabile n volte si dice che la funzione è di classe Cⁿ(I) nell'insieme di definizione I. $$ f \ ⊂ \ C^n(I) $$

La funzione f(x) che verifica un'equazione differenziale si chiama soluzione o integrale dell'equazione.

Risolvere un'equazione differenziale vuol dire trovare tutte le sue soluzioni. O perlomeno studiare il suo comportamento.

Una soluzione di una equazione differenziale è una funzione y(x) di classe Cⁿ(I) in un intervallo I∈R, cioé che ammette derivate continue fino all'ordine n nell'intervallo I, tale che per ogni x∈I è soddisfatta la relazione dell'equazione differenziale.

Esistono due tipi di soluzioni

• Soluzione generale (o integrale generale)
  E' l'insieme di tutte le funzioni y(x) che risolvono l'equazione differenziale. In pratica, la soluzione generale è una famiglia di funzioni del tipo F(x)+c.

  Esempio. L'equazione differenziale $$ y' = 2x-1 $$ ha la seguente soluzione generale $$ y =x^2+c $$ La soluzione generale è una famiglia di funzioni perché il parametro c∈R è un numero qualsiasi.

• Soluzione particolare
  E' una singola funzione y(x) che risolve l'equazione differenziale. In altre parole, il parametro c assume un valore costante specifico. Il grafico di ogni soluzione è detto curva integrale.

  Esempio. L'equazione differenziale $$ y' = 2x-1 $$ ha la seguente soluzione particolare $$ y =x^2+1 $$ In questo caso il parametro c è una costante uguale a uno ossia c=1. Quindi, si tratta di una singola funzione e non di una famiglia di funzioni. Un'altra soluzione particolare la ottengo fissando c=2 $$ y = x^2+2 $$ Entrambe le soluzioni particolari appartengono alla famiglia di funzioni della soluzione generale y=x²+c dell'equazione differenziale. E via dicendo.

A cosa servono le equazioni differenziali

Le equazioni differenziali mi aiutano a risolvere i problemi in cui non conosco la funzione incognita u(x) ma ho diverse informazioni sul suo comportamento.

$$ u(x) = ? $$

Capita spesso nello studio della fisica.

Ad esempio, conosco il tasso di crescita al variare di x, ossia la sua derivata prima u'(x)

$$ u'(x) $$

Grazie a questa informazione posso trovare la famiglia di funzioni U(x)+k che hanno lo stesso comportamento ossia lo stesso tasso di crescita u'(x).

Nota. Per questa ragione le equazioni differenziali non hanno mai una sola soluzione ma infinite soluzioni.

Un esempio pratico

Non conosco la funzione u(x) ma so che la funzione ha un tasso di crescita pari a 2 ossia la sua derivata prima è uguale a 2x.

$$ u'(x)=2x $$

La famiglia di funzioni che hanno questa caratteristica è individuata dall'integrale di u'(x)

$$ \int u'(x) \: dx = U(x) + k $$

In questo caso la soluzione generale (o integrale generale) dell'equazione differenziale è

$$ \int 2x \: dx = x^2 + k $$

Dove k è una costante reale qualsiasi.

Essendo k una costante reale può assumere qualsiasi valore, quindi l'equazione differenziale ha infinite soluzioni.

Nota. Il risultato è una famiglia di funzioni U(x)+k che si distinguono tra loro per il valore di una costante k. Poiché k può avere qualsiasi valore, la famiglia è composta da infinite funzioni. Tutte hanno però il medesimo comportamento ossia la stessa derivata prima. Ogni singola funzione è detta soluzione particolare dell'equazione differenziale. Ad esempio, la funzione u(x)=x²+1 dove la costante c=1 è una soluzione particolare. La funzione u(x)=x²+2 dove c=2 è un'altra soluzione particolare. E via dicendo.

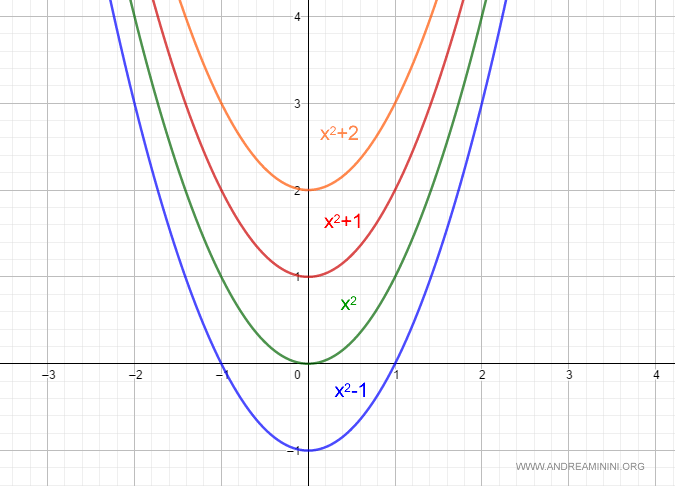
In generale l'equazione differenziali ha infinite soluzioni dipendenti da un numero di parametri uguali all'ordine dell'equazione

In questo caso c'è un solo parametro k perché l'equazione differenziale è del 1° ordine.

$$ \int 2x \: dx = x^2 + k $$

Ovviamente non tutte le equazioni differenziali sono così semplici.

L'esempio è utile soltanto per comprendere a cosa servono.

Come verificare la soluzione di un'equazione differenziale? Spesso risolvere un'equazione differenziale è molto difficile ma la verifica della soluzione è sempre molto semplice. Una volta trovata la funzione incognita u(x) basta calcolare le sue derivate e sostituirle nell'equazione differenziale. Ad esempio, la soluzione che ho appena trovato è u=x²+k. Derivo e sostituisco la soluzione nell'equazione differenziale $$ u'(x)=2x $$ $$ D_x[ x^2+k ]=2x $$ $$ 2x + 0 =2x $$ L'identità dell'equazione è soddisfatta. Pertanto, la soluzione è corretta.

Esempio 2

L'equazione differenziale

$$ u''=-u $$

Si risolve trovando una funzione che derivata due volte è uguale al suo opposto.

Sono soluzioni valide

$$ u(x)=k \cdot \sin(x) \\ u(x)=k \cdot \cos(x) \\ u(x)=a \cdot \sin(x)+b \cdot \cos(x) \\ \vdots $$

Oltre a queste c'è anche la soluzione costante u(x)=0

$$ u(x)=0 $$

Pertanto, la soluzione generale di un'equazione differenziale ha infinite soluzioni appartenenti a una o più famiglie di funzioni diverse tra loro.

Esempio 3

Faccio un altro esempio più complesso per rendere più chiaro il concetto.

In questa equazione differenziale la somma della derivata prima f'(x) e della derivata seconda f"(x) moltiplicata per tre è uguale a 9x.

$$ f'(x)+3f''(x)=9x $$

Il problema consiste nel trovare la funzione f(x) che soddisfi la precedente equazione.

Nota. In questo caso non basta calcolare l'integrale per trovare la soluzione. L'equazione differenziale è molto più complessa rispetto alla precedente.

Forma esplicita e forma implicita

Un'equazione differenziale è detta in forma esplicita o normale se è esplicitata rispetto alla derivata di ordine massimo y⁽ⁿ⁾

$$ y^{n} = f(x,y,y',...,y^{n-1}) $$

Dove f è una funzione reale di n+1 variabili reali definita in Rⁿ⁺¹.

In alternativa, la stessa equazione differenziale posso esprimerla in forma implicita

$$ F(x,y,y',...,y^{n}) = 0 $$

Dove F è una funzione reale di n+2 variabili reali definita in Rⁿ⁺².

In questo caso non è esplicitata la derivata di ordine massimo.

Ordine o grado dell'equazione differenziale

L'ordine (o grado) di un'equazione differenziale è la derivata di ordine massimo.

La derivata di ordine massimo (n) nell'equazione differenziale determina il grado dell'equazione differenziale.

Le più frequenti sono le seguenti:

• Equazione differenziale del primo ordine
• Equazione differenziale del secondo ordine
• Equazione differenziale del terzo ordine o superiore

Esempio 1

In questa equazione differenziale l'ordine di derivazione più alto è la derivata prima

$$ f'(x)+9x=5 $$

Quindi, si tratta di un'equazione differenziale del primo ordine (o primo grado)

Esempio 2

In questa equazione differenziale la derivata di ordine più alto è la derivata seconda

$$ f'(x)+3f''(x)+9x=5 $$

Pertanto, si tratta di un'equazione differenziale di secondo ordine (o secondo grado).

L'equazione differenziale omogenea, non omogenea e in forma normale

L'equazione differenziale è detta

• equazione differenziale omogenea
  se il termine noto dell'equazione differenziale è zero $$ F(x,y, y',...,y^{(n)} )=0 $$
• equazione differenziale non omogenea
  se il termine noto non è uguale a zero $$ F(x,y, y',...,y^{(n)} ) \ne 0 $$
• equazione differenziale in forma normale
  se l'equazione differenziale è esplicitata rispetto alla derivata di ordine più elevato $$ y^{(n)} = f(x,y, y',...,y^{(k-1)}) $$

Tipi di equazioni differenziali

Oltre all'ordine di derivazione le equazioni differenziali si distinguono in

• equazioni differenziali ordinarie (EDO)
  Sono equazioni con derivate di funzioni di una variabile reale
• equazioni differenziali alle derivate parziali
  Sono equazioni in cui appaiono derivate parziali di funzioni di due variabili reali f(x,y)

  Esempio. Un esempio di equazione differenziale con derivate parziali $$ \frac{d''u(x,y)}{dx^2} + \frac{d''u(x,y)}{dy^2} = 0 $$

Un'altra classificazione molto usata è tra

• Equazioni differenziali lineari
  Sono equazioni in cui sussiste una relazione lineare tra le derivate della funzione incognita y(x)
• Equazioni differenziali non lineari
  Sono equazioni con una relazione non lineare tra le derivate della funzione incognita y(x)

  Esempio. Un esempio di equazione differenziale non lineare del primo ordine è la seguente $$ y'=y^2 $$

Come risolvere un'equazione differenziale

Non c'è un unico metodo risolutivo perché esistono diverse tipologie di equazioni differenziali e ognuna richiede un metodo di risolutivo a se stante.

Equazioni differenziali del primo ordine

Sono le equazioni differenziali in cui la derivata prima è l'ordine di derivazione più alto.

• Equazioni differenziali elementari
• Equazioni differenziali a variabili separate
• Equazioni differenziali lineari

Equazioni differenziali del secondo ordine

Sono le equazioni differenziali in cui la derivata seconda è l'ordine di derivazione più alto.

• Equazioni differenziali elementari del 2° ordine
• Equazioni differenziali lineari omogenee
• Equazioni differenziali lineari complete
• Equazioni differenziali senza la funzione incognita

E così via.