Equazioni lineari

Un'equazione lineare è un'equazione di primo grado con un'incognita $$ a \cdot x = b $$ o più incognite $$ a \cdot x + b \cdot y = c $$.

Equazione lineare con una incognita

La soluzione di un'equazione lineare con un'incognita ax=b è un valore da assegnare alla variabile x che rende uguale il primo e il secondo membro dell'equazione.

Esempio. L'equazione lineare $$ 6 = x \cdot 3 $$ ha una soluzione x=2 che si ottiene esplicitando la x rispetto al resto. $$ x = \frac{6}{3} $$ $$ x = 2 $$

Equazione lineare con due incognite

Nelle equazioni lineari con due incognite

$$ a \cdot x + b \cdot y = c $$

la soluzione è una coppia di valori (x;y) che eguaglia il primo e il secondo membro.

Esempio. L'equazione lineare $$ 2y + x = 6 $$ ha infinite soluzioni. Le posso trovare esplicitando la y rispetto alla x $$ y = \frac{6-x}{2} $$ Una volta trovata l'equazione esplicita, basta assegnare un qualsiasi valore alla x per ottenere il valore corrispondente della variabile y. Ecco alcune soluzioni: (0;3) , (2;2) , (6;0), ecc.

Le equazioni lineari a due variabili hanno infinite soluzioni. Quindi, sono equazioni indeterminate.

Come risolvere un'equazione di primo grado

Un’equazione di primo grado numerica intera nell’incognita $x$ è un’uguaglianza fra due espressioni algebriche in cui l’incognita compare al massimo con esponente 1. Ha la forma generale:

$$ ax + b = cx + d $$

Dove $a, b, c, d$ sono numeri interi (coefficienti positivi, negativi o nulli) e $x$ è l’incognita da determinare.

Vediamo, passo per passo, come si risolve questo tipo di equazione.

1] Svolgere i calcoli e rendere interi i coefficienti

Se nell’equazione compaiono delle frazioni, il primo passo è eliminare i denominatori.

Trovo il minimo comune multiplo (m.c.m.) dei denominatori e moltiplico entrambi i membri per questo valore.

In questo modo si ottiene un’equazione con soli coefficienti interi.

Esempio. Considero l'equazione iniziale $$ \frac{2}{3}x - \frac{5}{2} = \frac{1}{6}x + 1 $$ Il m.c.m. dei denominatori $3, 2, 6$ è 6. Moltiplico entrambi i membri per 6: $$ 6 \cdot \left(\frac{2}{3}x - \frac{5}{2}\right) = 6 \cdot \left(\frac{1}{6}x + 1\right) $$ Svolgo i calcoli: $$ 4x - 15 = x + 6 $$ Ora l’equazione ha coefficienti interi.

2] Trasportare i termini con $x$ a un membro e i numeri all’altro

Sposto tutti i termini contenenti $x$ al primo membro dell'equazione e i termini numerici al secondo membro, cambiando di segno quelli trasportati.

Poi riduco eventuali termini simili.

Esempio. Riprendo l’equazione precedente: $$ 4x - 15 = x + 6 $$ Trasporto $x$ al primo membro e $-15$ al secondo: $$ 4x - x = 6 + 15 $$ Riducendo i termini simili ottengo: $$ 3x = 21 $$

3] Risolvere l’equazione del tipo $ax = b$

L’equazione ora è ridotta alla forma $ax = b$.

A questo punto, si risolve facilmente dividendo entrambi i membri per il coefficiente di $x$.

Esempio. Partendo da: $$ 3x = 21 $$ Divido per 3: $$ x = \frac{21}{3} $$ Quindi, la soluzione dell'equazione è: $$ x = 7 $$

4] Verifica

Una volta ottenuta la soluzione, è sempre buona norma sostituire il valore trovato nell’equazione iniziale per verificare che sia corretto.

Esempio. Sostituisco $x = 7$ nell’equazione iniziale: $$ \frac{2}{3} \cdot 7 - \frac{5}{2} = \frac{1}{6} \cdot 7 + 1 $$ Calcolo  entrambi i membri: $$ \frac{14}{3} - \frac{5}{2} = \frac{7}{6} + 1 $$ Trasformo in numeri decimali per semplicità: $$
4.\overline{6} - 2.5 = 1.16\overline{6} + 1 $$ $$ 2.16\overline{6} = 2.16\overline{6} $$ La verifica è soddisfatta.

Seguendo questi tre passi si può risolvere qualsiasi equazione di primo grado numerica intera nell’incognita $x$.

Le equazioni determinate, indeterminate e impossibili

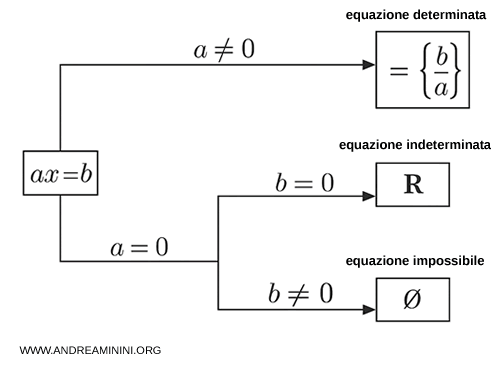
Un’equazione di primo grado è determinata quando possiede una sola soluzione reale.

In questi casi il coefficiente della variabile è diverso da zero, perciò possiamo risolvere dividendo entrambi i membri per quel coefficiente.

Ad esempio, considero l'equazione di 1°: $$ 2x = 10 $$ In questo caso $ a=2 $ e $ b = 10 $. Divido per 2 e ottengo: $$ x = \frac{10}{2} = 5 $$  L'equazione ha una sola soluzione, $x = 5$.

Un’equazione è indeterminata (o identità) quando è vera per ogni valore reale di $x$.

Questo accade, ad esempio, se la variabile è moltiplicata per zero ( $ a= 0 $ ) e il secondo membro è anch’esso zero ( $ b = 0 $ ).

Ad esempio, questa equazione è una identità $$ 0 \cdot x = 0 $$ Qualsiasi valore di $x$ moltiplicato per zero dà zero, quindi ogni numero reale è soluzione. Pertanto, l’insieme delle soluzioni è $\mathbb{R}$.

Un’equazione è impossibile quando nessun valore di $x$ la verifica.

Succede, ad esempio, se la variabile è moltiplicata per zero $ ( a=0 $), ma il secondo membro è diverso da zero ( $ b \ne = 0 $ ) ossia $ 0 \cdot x = b $

Ad esempio, questa equazione è impossibile $$ 0 \cdot x = 5 $$ Qualunque numero moltiplicato per zero dà zero, mai 5. Nessuna soluzione esiste. In questo caso, l’insieme delle soluzioni è vuoto $\varnothing$.

E così via.