La parabola

Una parabola è una curva algebrica piana del 2° ordine, definita come l'insieme di tutti i punti che sono equidistanti da un punto fisso chiamato fuoco (F) e da una retta fissa (d) chiamata direttrice non passante per il punto F.

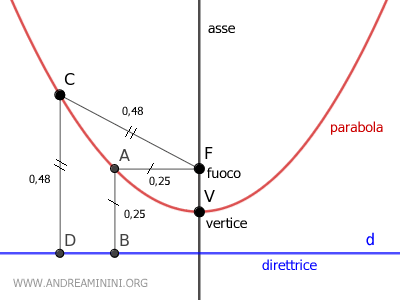
In altre parole, i punti della parabola formano un luogo geometrico perché sono i punti del piano che soddisfano la proprietà di avere la stessa distanza dal fuoco (F) e dalla retta direttrice (d) della parabola.

L'asse della parabola è la retta che passa per il fuoco e perpendicolare alla direttrice.

Il vertice della parabola è il punto di intersezione tra l'asse della parabola e la parabola stessa.

Una parabola può essere definita anche come la superficie (sezione conica) ottenuta tagliando un cono circolare indefinito con un piano parallelo alla retta generatrice del cono.

 

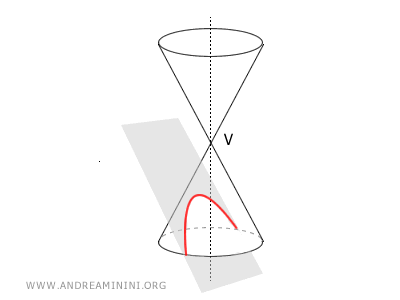
Nota. La parabola ha diverse applicazioni in fisica, ingegneria e altre scienze. Ad esempio, in fisica può descrivere la traiettoria del lancio di un grave in assenza di resistenza dell'aria.

L'equazione della parabola

La forma standard dell'equazione di una parabola con l'asse di simmetria parallelo all'asse y è la seguente:

$$ y = ax^2 + bx + c $$

Dove a,b e c sono coefficienti reali costanti con a diverso da zero (a≠0).

Nota. L'apertura della parabola dipende dal valore assoluto del coefficiente "a". All'aumentare del valore assoluto |a| si riduce l'apertura della parabola rispetto al proprio asse, e viceversa. Il segno del coefficiente "a" determina anche la concavità/convessità della parabola. Se a>0 la parabola è rivolta verso l'alto (convessa), se a<0 la parabola è rivolta verso il basso (concava).

Se l'asse di simmetria è orizzontale, l'equazione standard è:

$$ x = ay^2 + by + c $$

Le principali componenti di una parabola sono le seguenti

• Fuoco
  Il fuoco (F) è un punto fisso all'interno della parabola. Le coordinate del fuoco si ottengono in questo modo $$ F \begin{pmatrix} - \frac{b}{2a} \ , \ \frac{1-Δ}{4a} \end{pmatrix} $$ Dove a,b,c sono i coefficienti dell'equazione della parabola y=ax²+bx+c e il discriminante Δ=b²-4ac
• Direttrice
  La direttrice (d) è una retta fissa esterna alla parabola. L'equazione della retta direttrice è la seguente: $$ y= - \frac{1+Δ}{4a} $$
• Asse
  L'asse è una retta perpendicolare alla retta direttrice (d) passante per il punto di fuoco (F) della parabola. L'asse della parabola è anche un asse di simmetria perché la divide in due parti speculari. L'equazione dell'asse è la seguente: $$ x= - \frac{b}{2a} $$
• Il vertice
  Il vertice (V) è il punto in cui la parabola interseca l'asse. Nel vertice la parabola raggiunge il suo valore massimo o minimo a seconda del segno del coefficiente "a" dell'equazione della parabola y=ax²+bx+c. Le coordinate del vertice si posso calcolare nel modo seguente $$ V \begin{pmatrix} - \frac{b}{2a} \ , \ - \frac{Δ}{4a} \end{pmatrix} $$

Un esempio pratico

Considero l'equazione della seguente parabola

$$ y = 2x^2 -4x + 3 $$

I coefficienti reali dell'equazione sono a=2, b=-4 e c=3.

Dal segno positivo del coefficiente a=2 capisco subito che la parabola è rivolta verso l'alto.

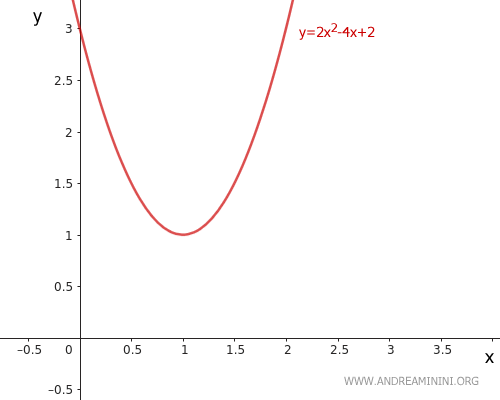
Utilizzo la formula per determinare la retta direttrice della parabola.

$$ y= - \frac{1+Δ}{4a} $$

Sapendo che a=2, b=-4 e c=3, il discriminante Δ=b²-4ac è il seguente

$$ \Delta = b^2 - 4ac = (-4)^2-4 \cdot 2 \cdot 3 = 16- 24 = -8 $$

Quindi l'equazione della retta direttice è

$$ y= - \frac{1+Δ}{4a} = - \frac{1-8}{4 \cdot 2} = - \frac{-7}{8} = \frac{7}{8} $$

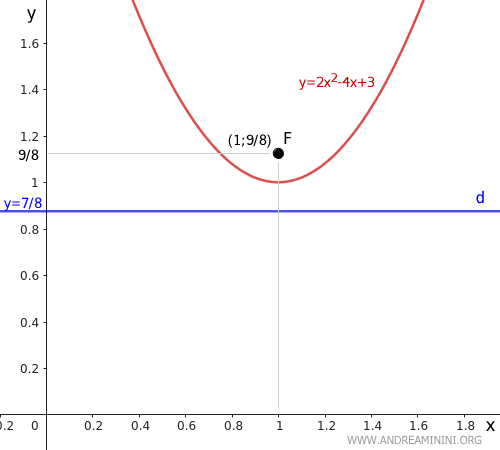
Aggiungo la retta direttrice (d) y=7/8 nel grafico

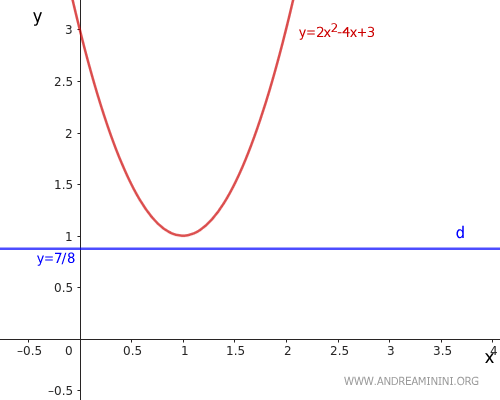
Ora calcolo il punto di fuoco (F) della parabola.

$$ F \begin{pmatrix} - \frac{b}{2a} \ , \  \frac{1-Δ}{4a} \end{pmatrix} $$

Sostituisco a=2, b=-4, c=3 e il discriminante che già conosco Δ=-8

$$ F \begin{pmatrix} - \frac{-4}{2 \cdot 2} \ , \  \frac{1-(-8)}{4 \cdot 2} \end{pmatrix} $$

$$ F \begin{pmatrix} - \frac{-4}{4} \ , \  \frac{9}{8} \end{pmatrix} $$

$$ F \begin{pmatrix} 1 \ , \  \frac{9}{8} \end{pmatrix} $$

Quindi, il punto di fuoco F della parabola si trova alle coordinate del piano (x;y)=(1,9/8).

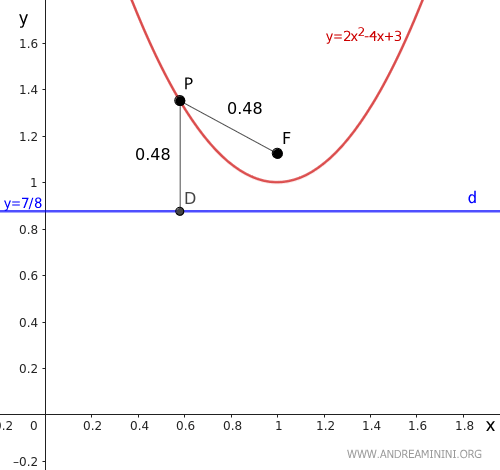
Per fare una rapida verifica, prendo un punto qualsiasi P e misuro la distanza rispetto al fuoco F e alla retta direttrice d.

La distanza è la stessa PF≅PD, quindi il calcolo è corretto.

A questo punto calcolo l'equazione dell'asse della parabola.

$$ x= - \frac{b}{2a} $$

Sapendo che a=2 e b=-4 il calcolo è molto semplice

$$ x= - \frac{-4}{2 \cdot 2} = - \frac{-4}{4} = 1 $$

Quindi, l'asse della parabola è una retta verticale, parallela all'asse delle ordinate, che passa per l'ascissa x=1.

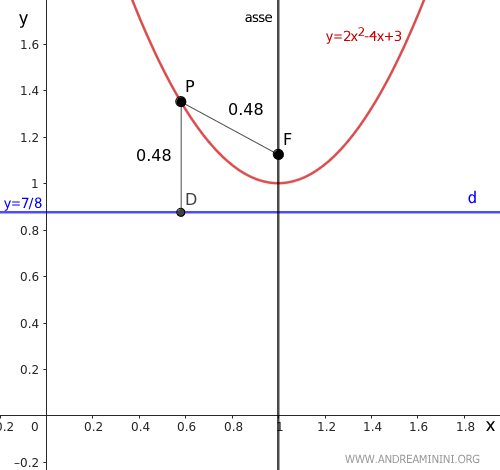
Per definizione l'asse è perpendicolare alla retta direttrice (d) e passa per il vertice (V) della parabola.

Nel caso della parabola l'asse è anche l'asse di simmetria della curva.

Questo vuol dire che per ogni punto P esiste un altro punto P' che ha la stessa distanza dal fuoco (F) e dalla retta direttrice (d).

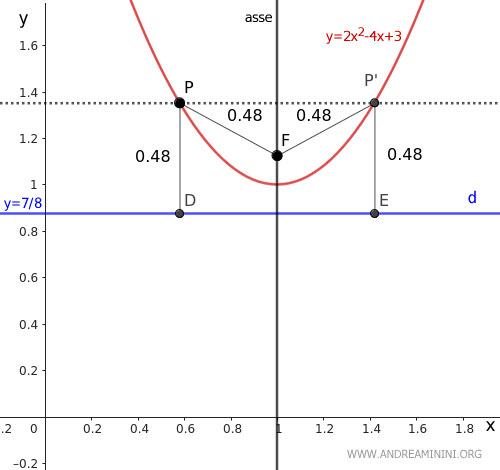
A questo punto mi restano solo da calcolare le coordinate del vertice (V) della parabola e sperare che sia un punto appartenente all'asse.

$$ V \begin{pmatrix} - \frac{b}{2a} \ , \ - \frac{Δ}{4a} \end{pmatrix} $$

Sapendo che a=2, b=-4, c=3 e il discriminante è Δ=-8

$$ V \begin{pmatrix} - \frac{-4}{2 \cdot 2} \ , \ - \frac{-8}{4 \cdot 2} \end{pmatrix} $$

$$ V \begin{pmatrix} - \frac{-4}{4} \ , \ - \frac{-8}{8} \end{pmatrix} $$

$$ V \begin{pmatrix} 1 \ , 1 \end{pmatrix} $$

Il vertice V si trova alle coordinate del piano (x;y)=(1;1).

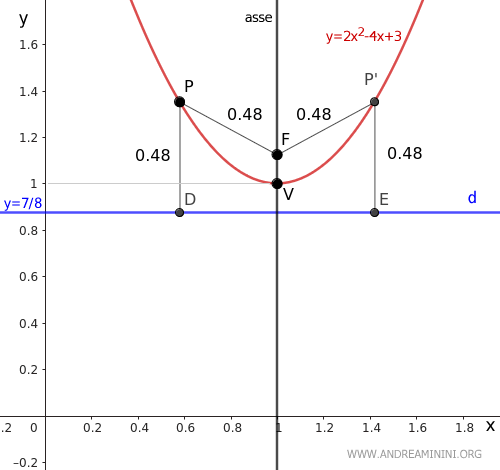
Il vertice V della parabola è un punto dell'asse. Quindi, il calcolo è corretto.

 

Il grafico di una parabola

Il grafico di una parabola è il grafico di una funzione quadratica che del tipo $$ y = ax^2+bx+c $$ con a≠0 diverso da zero. E' una curva algebrica piana del secondo ordine, aperta e simmetrica rispetto al proprio asse.

L'equazione di una parabola è

$$ y = ax^2 + bx + c $$

Dal punto di vista grafico ogni parabola è caratterizzata da un asse di simmetria.

= ay^2 + by + c

Presi due punti qualsiasi A e B della parabola con pari ordinata, questi sono punti simmetrici ed equidistanti dall'asse di simmetria

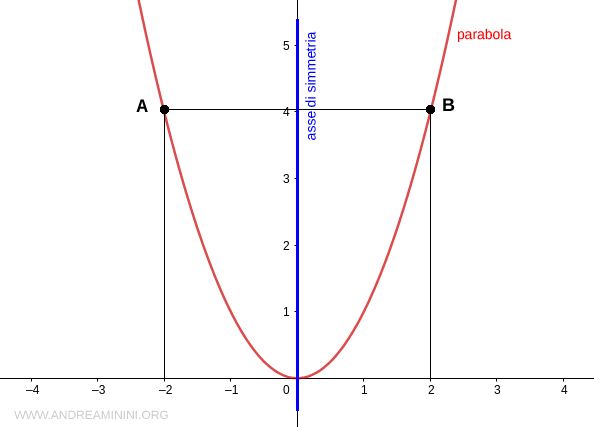
Sono equidistanti anche da qualsiasi altro punto fisso dell'asse di simmetria detto fuoco (F).

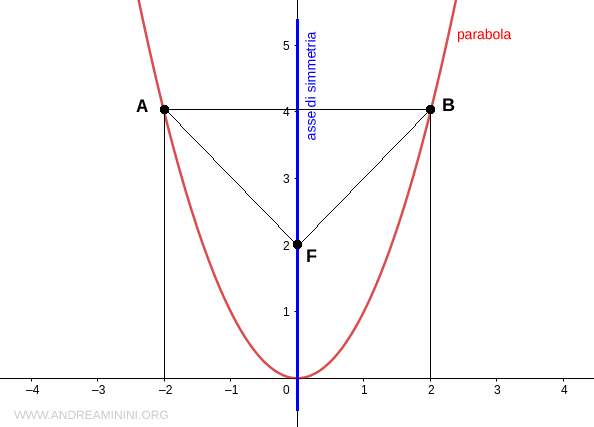
Il punto in cui il grafico della parabola interseca l'asse di simmetrica è detto vertice (V) della parabola.

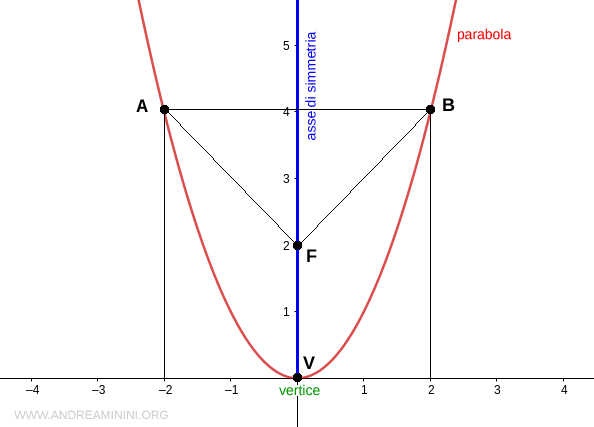
Nel caso in cui l'equazione della parabola è y=ax² il vertice della parabola coincide con l'origine O(0;0) del piano cartesiano.

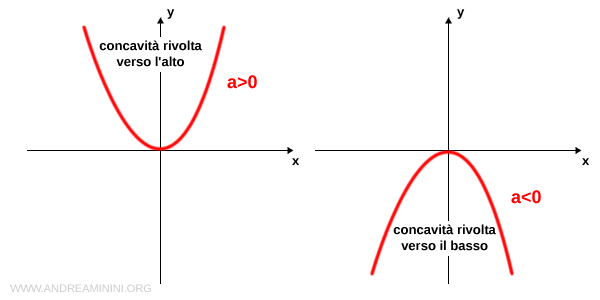
Il segno del coefficiente a determina la concavità della parabola.

• a>0
  se a>0 la parabola ha la concavità rivolta verso l'alto
• a<0
  se a<0 la parabola ha la concavità rivolta verso il basso

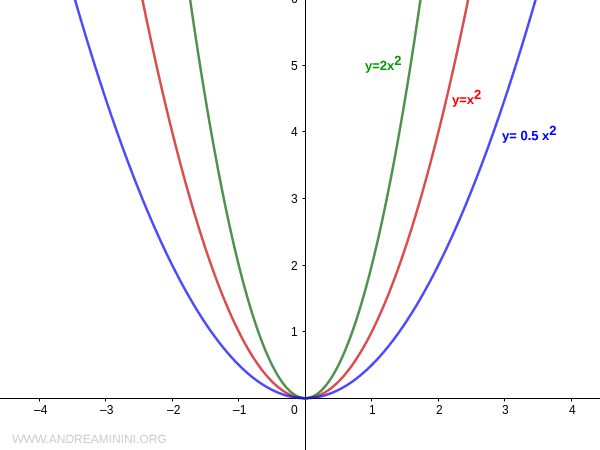
Il valore assoluto del coefficiente |a| determina l'ampiezza della parabola.

Quanto maggiore è il valore assoluto |a| tanto minore è l'apertura della parabola.

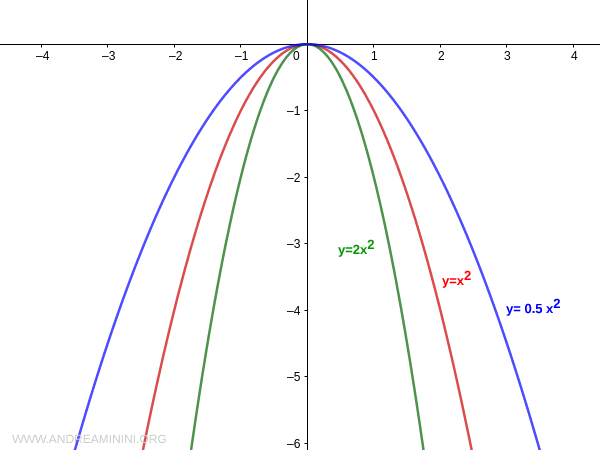
Lo stesso accade se il coefficiente a è negativo

Nota. Il coefficiente a dell'equazione di una parabola deve essere diverso da zero perché se fosse uguale a zero la funzione avrebbe il grafico di una funzione costante

Osservazioni

Alcune osservazioni e note personali a margine sulle parabole

• La parabola è una sezione conica
  La parabola è una delle sezioni coniche, insieme all'iperbole, all'ellisse e al cerchio. Nel caso della parabola, il cono viene tagliato da un piano parallelo alla retta genetrice del cone e interseca una sola falda del cono. Pertanto, la parabola si presenta come una curva aperta e illimitata.
  

  

• L'asse della parabola è anche l'asse di simmetria della curva
  Questo significa che per ogni punto sulla parabola, c'è un altro punto sulla stessa che è simmetrico al primo rispetto a questo asse.
• Apertura della parabola e valore assoluto del coefficiente "a"
  L'apertura della parabola è determinata dal valore assoluto del coefficiente "a" dell'equazione y=ax²+bx+c della parabola. Quando ∣a∣ è grande, la parabola tende ad aprirsi meno, cioè è più "stretta". Al contrario, quando ∣a∣ è piccolo, la parabola tende ad aprirsi di più, cioè è più "larga".
  

  

• Concavità verso l'alto o verso il basso e segno del coefficiente "a"
  Il segno del coefficiente "a" dell'equazione y=ax²+bx+c della parabola determina la direzione in cui la parabola si apre. Se a>0 la parabola si apre verso l'alto, ed è quindi concava verso l'alto. Se a<0, la parabola si apre verso il basso, ed è concava verso il basso.
  

  

  Nota. Una curva è definita come concava se il segmento che collega due punti della curva giace completamente al di sotto della curva.

• Proprietà ottica della parabola
  In una parabola, se traccio la tangente (t) di un punto P della curva, la perpendicolare (n) della tangente divide in due angoli congruenti $ \alpha \cong \beta $ l'angolo formato dal raggio focale $ PF $ e dalla semiretta $ PQ $ parallela all'asse focale
  
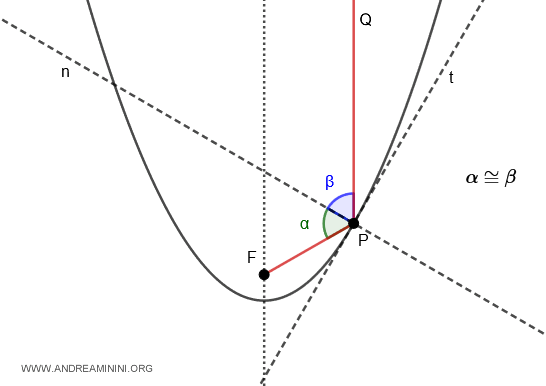
  Questo significa che in uno specchio parabolico, qualsiasi raggio parallelo all'asse focale viene riflesso in direzione del punto focale (F). Quindi, tutti i raggi paralleli all'asse focale vengono concentrati in un unico punto di ricezione. Questo principio è alla base delle antenne paraboliche satellitari e dei pannelli solari a concentrazione.
  
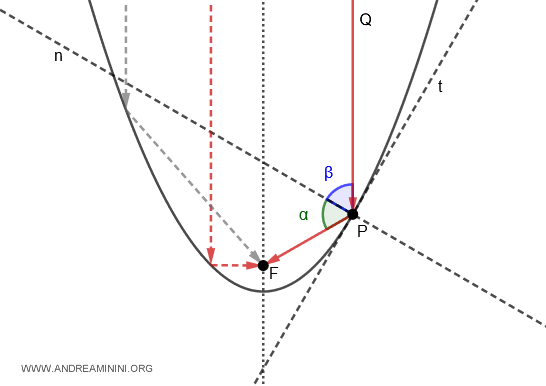
  Viceversa, se il punto focale (F) è una sorgente luminosa, tutti i raggi riflessi dallo specchio parabolico sono paralleli all'asse focale.
  

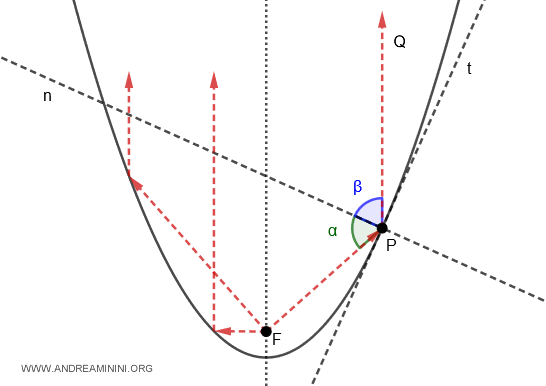
E così via.