Sistema di equazioni fratto
Un sistema di equazioni è detto sistema fratto o frazionario se include almeno una delle incognite compare al denominatore di una frazione.
Come si risolve un sistema di equazioni fratto
Per risolvere questo tipo di sistema
- Verifico le condizioni di esistenza per ricondurre il sistema a un sistema di equazioni intero
- Trovo le soluzioni del sistema intero (se esistono)
- Elimino le soluzioni del sistema intero che non soddisfano le condizioni di esistenza del sistema fratto
- Le soluzioni restanti sono le soluzioni del sistema fratto
Un esempio pratico
Questo sistema è un sistema di equazioni fratto perché la prima equazione è un'equazione fratta
$$ \begin{cases} \frac{2}{x}+ \frac{1}{y} =0 \\ \\ 8x+15y=1 \end{cases} $$
La condizione di esistenza (C.E.) del sistema fratto è x≠0 e y≠0
$$ C:E: \ : \ x \ne 0 \ ∧ \ y \ne 0 $$
Applico la proprietà invariantiva delle equazioni moltiplicando entrambi i membri della prima equazione per xy
$$ \begin{cases} xy \cdot ( \frac{2}{x}+ \frac{1}{y} ) = xy \cdot 0 \\ \\ 8x+15y=1 \end{cases} $$
$$ \begin{cases} xy \cdot \frac{2}{x} + xy \cdot \frac{1}{y} = 0 \\ \\ 8x+15y=1 \end{cases} $$
$$ \begin{cases} 2y + x = 0 \\ \\ 8x+15y=1 \end{cases} $$
In questo modo ottengo un sistema di equazioni intero.
Nota. In alternativa avrei potuto calcolare il minimo comune multiplo del denominatore nella prima equazione. Il risultato è sempre lo stesso. $$ \begin{cases} \frac{2y+x}{xy} =0 \\ \\ 8x+15y=1 \end{cases} $$ $$ \begin{cases} 2y+x =0 \\ \\ 8x+15y=1 \end{cases} $$
Risolvo il sistema di equazioni con il metodo della sostituzione.
Esplicito la variabile x nella prima equazione e sostituisco x=-2y nella seconda equazione del sistema.
$$ \begin{cases} x = -2y \\ \\ 8x+15y=1 \end{cases} $$
$$ \begin{cases} x = -2y \\ \\ 8 \cdot (-2y) +15y =1 \end{cases} $$
$$ \begin{cases} x = -2y \\ \\ -16y +15y =1 \end{cases} $$
$$ \begin{cases} x = -2y \\ \\ -y =1 \end{cases} $$
$$ \begin{cases} x = -2y \\ \\ y =-1 \end{cases} $$
Una volta trovata l'incognita y nella seconda equazione, sostituisco y=-1 nella prima equazione
$$ \begin{cases} x = -2 \cdot (-1) \\ \\ y =-1 \end{cases} $$
$$ \begin{cases} x =2 \\ \\ y =-1 \end{cases} $$
Pertanto, la soluzione del sistema intero è x=2 e y=-1.
$$ (x;y) = (2;-1) $$
Questa soluzione è anche la soluzione del sistema fratto perché soddisfa la condizione di esistenza x≠0 e y≠0
$$ \begin{cases} x =2 \\ \\ y =-1 \\ \\ x \ne 0 \\ \\ y \ne 0 \end{cases} $$
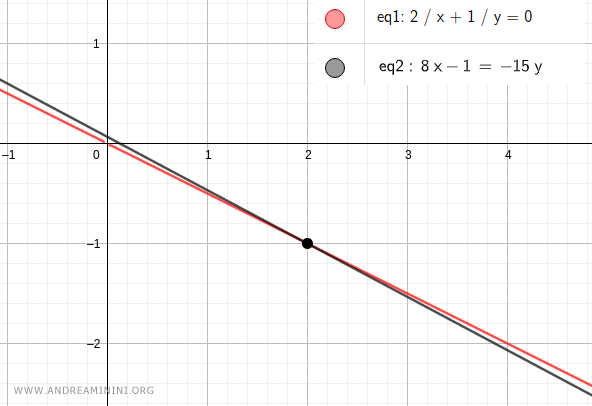
Verifica. Per verificare il risultato rappresento le due equazioni del sistema fratto sul piano cartesiano. Come previsto le rette si intersecano nel punto (x;y)=(2;-1). La soluzione del sistema fratto è corretta.
E così via.
