Sistema letterale di equazioni
Un sistema di equazioni è detto sistema letterale se include almeno un'equazione è letterale.
Un'equazione è letterale se include uno o più parametri oltre alle variabili incognite.
I parametri sono costanti indefinite che possono assumere diversi valori.
Nota. In genere, pur non essendoci alcuna convenzione sulla notazione, i parametri sono indicati con le prime lettere minuscole a,b,c,k,ecc. dell'alfabeto. Le variabili incognite di un'equazione sono invece indicate con le ultime lettere minuscole x,y,z dell'alfabeto.
Un esempio pratico
Considero il sistema letterale
$$ \begin{cases} x+2y=4 \\ \\ ax+y=2 \end{cases} $$
Risolvo il sistema con il metodo del confronto
$$ \begin{cases} y=\frac{4-x}{2} \\ \\ y=2-ax \end{cases} $$
Metto a confronto le due equazioni y=y
$$ \frac{4-x}{2} = 2-ax $$
$$ 4-x = 2 \cdot (2-ax) $$
$$ 4-x = 4-2ax $$
$$ -x - 2ax = 4 $$
$$ x \cdot (2a-1) = 4 $$
La componente (2a-1) si annulla quando a=1/2
$$ a = \frac{1}{2} $$
In questo caso l'equazione non si verifica perché qualsiasi valore della x moltiplicato per 0 non può essere uguale a 4.
Pertanto, per a=1/2 il sistema di equazioni non ha soluzioni ossia è impossibile.
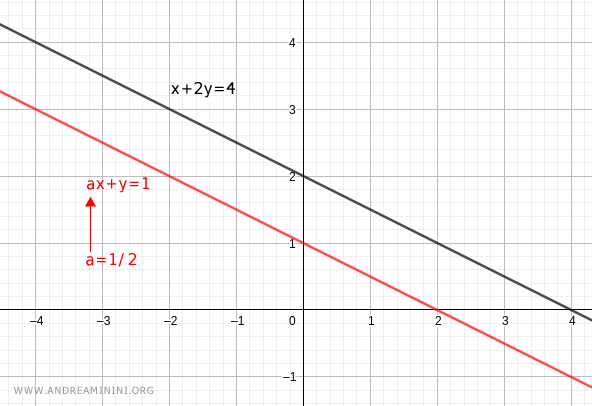
Nota. Quando a=1/2 le rette delle due equazioni del sistema sono parallele. Non avendo punti in comune il sistema non ha soluzioni.
Viceversa, per qualsiasi altro valore a≠1/2 il sistema di equazioni ha una soluzione, ossia è determinato.
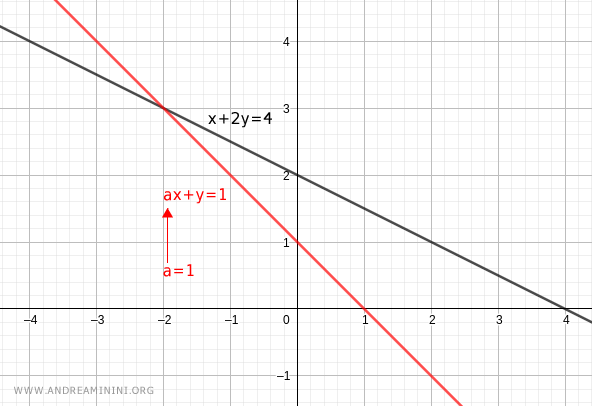
E così via.
