La regola di Cartesio
- In un'equazione di secondo grado in forma normale ax2+bx+c=0 con discriminante non negativo Δ≥0
- a ogni permanenza del segno corrisponde una radice negativa
- a ogni variazione del segno corrisponde una radice positiva
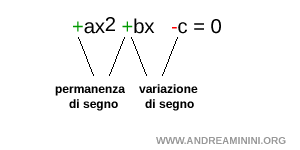
Una permanenza del segno si verifica quando i coefficienti a,b oppure b,c hanno lo stesso segno.
Viceversa, se il segno è diverso si verifica una variazione.
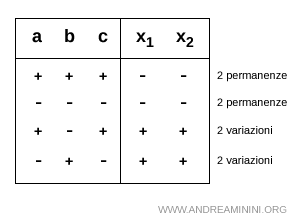
Quindi, le radici di un'equazione di 2° grado sono concordi, hanno lo stesso segno, soltanto se si verificano due permanenze di segno (radici negative) o due variazioni di segno (radici positive).
Negli altri casi le radici sono discordi, ossia hanno segno diverso.
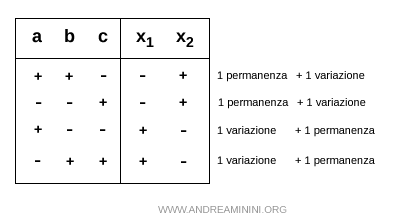
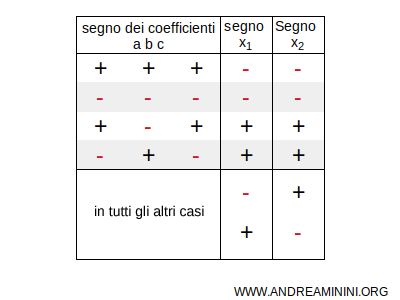
Quindi, in generale la tabella dei segni delle radici ottenute tramite il metodo di Cartesio è la seguente

Nel caso delle radici x1 e x2 di segno opposto
- Se la variazione precede la permanenza, la radice in valore assoluto maggiore è quella positiva.
- Se la permanenza precede la variazione, la radice in valore assoluto maggiore è quella negativa.
A cosa serve? La regola di Cartesio mi permette di capire qual è il segno delle radici reali di un'equazione di 2° grado senza doverla risolvere.
Un esempio pratico
Considero l'equazione di 2° grado
$$ 4x^2-3x-1= 0 $$
I coefficienti sono a=4, b=-3, c=-1
Il discriminante è non negativo, quindi l'equazione ha soluzioni reali
$$ \Delta = b^2-4ac = (-3)^2 - 4(4)(-1) = 9 + 16 = 25 $$
Nei coefficienti dell'equazione c'è una variazione di segno seguita da una permanenza di segno (+--)
Pertanto, le radici dell'equazione sono discordi, hanno segno opposto.
Verifica. Calcolo le radici dell'equazione. $$ x = \frac{-b \pm \sqrt{\Delta}}{2a} $$ $$ x = \frac{-(-3) \pm \sqrt{25} }{2(4)} $$ $$ x= \frac{3 \pm 5}{8} = \begin{cases} x_1 = \frac{-1}{4} \\ \\ x_2 = 1 \end{cases} $$ Le radici hanno segno opposto. Nell'equazione 4x2-3x-1=0 la variazione di segno precede la permanenza di segno, pertanto la radice positiva x2=1 è in valore assoluto maggiore della radice negativa x1=-1/4.
La dimostrazione
Per dimostrare la regola di Cartesio suddivido la dimostrazione in vari casi
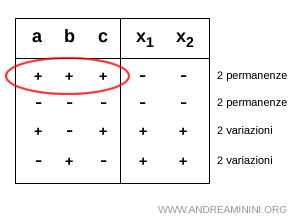
A] Doppia permutazione di segno +++
Nella doppia permutazione di segno positiva (+++) i coefficienti dell'equazione ax2+bx+c=0 sono positivi a>0, b>0 e c>0
In base alla regola del prodotto delle radici
$$ x_1 \cdot x_2 = \frac{c}{a} $$
Essendo a>0 e c>0 positivi, ne consegue che anche il prodotto delle radici è positivo x1x2>0
$$ a,c>0 \Rightarrow \frac{c}{a} >0 \Rightarrow x_1 \cdot x_2 > 0 $$
Da questo deduco che le radici x1 e x2 hanno lo stesso segno, sono entrambe positive o negative.
- x1, x2 >0
- x1, x2 <0
Resta da capire quale delle due ipotesi è giusta
In base alla regola della somma delle radici
$$ x_1 + x_2 = - \frac{b}{a}$$
Sapendo che b>0 e a>0 ne consegue che -b/a<0. Quindi, la somma delle radici è negativa x1+x2<0
$$ b,a>0 \Rightarrow - \frac{b}{a} < 0 \Rightarrow x_1 + x_2 < 0 $$
Sapendo che x1 e x2 hanno lo stesso segno, l'unica possibilità per avere una somma negativa x1+x2<0 è che x1 e x2 siano entrambe negative.
x1, x2 >0- x1, x2 <0
Nota. So già che le radici x1 e x2 hanno lo stesso segno. Se le radici fossero entrambe positive anche la loro somma sarebbe positiva x1+x2>0 ma questo viola la seconda condizione x1+x2<0. Quindi, per esclusione le radici sono entrambe negative.
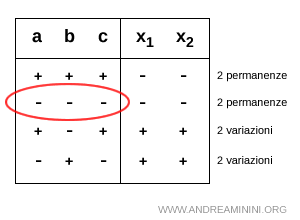
B] Doppia permutazione di segno ---
Nella doppia permutazione di segno negativa (---) i coefficienti dell'equazione ax2+bx+c=0 sono negativi a<0, b<0 e c<0
In base alla regola del prodotto delle radici
$$ x_1 \cdot x_2 = \frac{c}{a} $$
Essendo a<0 e c<0 negativi, ne consegue che il rapporto c/a>0 è positivo.
$$ a,c<0 \Rightarrow \frac{c}{a} >0 \Rightarrow x_1 \cdot x_2 > 0 $$
Quindi, anche il prodotto delle radici è positivo x1x2>0
Da questo deduco che le radici x1 e x2 hanno lo stesso segno, sono entrambe positive o negative.
- x1, x2 >0
- x1, x2 <0
In base alla regola della somma delle radici
$$ x_1 + x_2 = - \frac{b}{a}$$
Sapendo che b<0 e a<0 ne consegue che -b/a<0. Quindi, la somma delle radici è negativa x1+x2<0
$$ b,a<0 \Rightarrow - \frac{b}{a} < 0 \Rightarrow x_1 + x_2 < 0 $$
Da questo deduco che le radici x1 e x2 sono entrambe negative.
x1, x2 >0- x1, x2 <0
Nota. So già che le radici x1 e x2 devono avere lo stesso segno. Se le radici fossero entrambe positive anche la loro somma sarebbe positiva x1+x2>0 ma questo viola la seconda condizione x1+x2<0. Quindi, per esclusione le radici sono entrambe negative. E' l'unica possibilità in grado di soddisfare sia la regola del prodotto che la regola delle radici.
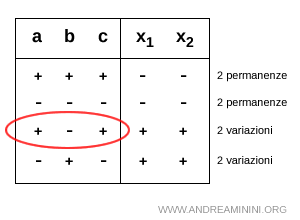
C] Doppia variazione di segno +-+
Nella doppia variazione di segno (+-+) i coefficienti dell'equazione ax2+bx+c=0 sono a>0, b<0 e c>0
Per la regola del prodotto sapendo che a,c>0
$$ a,c>0 \Rightarrow \frac{c}{a} >0 \Rightarrow x_1 \cdot x_2 > 0 $$
Pertanto, le radici possono essere entrambe positive o entrambe negative
- x1, x2 >0
- x1, x2 <0
Per la regola della somma, sapendo che a>0 e b<0, deduco che la somma x1+x2>0
$$ a>0,b<0 \Rightarrow - \frac{b}{a} > 0 \Rightarrow x_1 + x_2 > 0 $$
Questo mi permette di escludere il caso delle radici entrambe negative
- x1, x2 >0
x1, x2 <0
Pertanto, le radici sono entrambe positive.
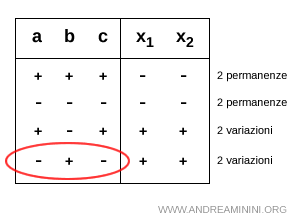
D] Doppia variazione di segno -+-
Nella doppia variazione di segno (-+-) i coefficienti dell'equazione ax2+bx+c=0 sono a<0, b>0 e c<0
Per la regola del prodotto, sapendo che a,c<0, il prodotto x1·x2>0
$$ a,c<0 \Rightarrow \frac{c}{a} >0 \Rightarrow x_1 \cdot x_2 > 0 $$
Pertanto, le radici sono entrambe positive o entrambe negative
- x1, x2 >0
- x1, x2 <0
Per la regola della somma, sapendo che a<0 e b>0, deduco che la somma x1+x2>0
$$ a<0,b>0 \Rightarrow - \frac{b}{a} > 0 \Rightarrow x_1 + x_2 > 0 $$
Quindi, escludo il caso delle radici entrambe negative
- x1, x2 >0
x1, x2 <0
Pertanto, le radici sono entrambe positive.
E] Una permanenza e una variazione di segno ++-
Nel caso di una permanenza iniziale di segno seguita da una variazione (++-) i coefficienti dell'equazione ax2+bx+c=0 sono a>0, b>0 e c<0
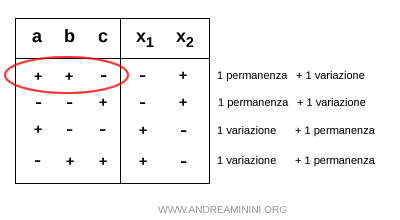
Per la regola del prodotto, sapendo che a>0, c<0 il prodotto x1·x2<0 è negativo
$$ a>0,c<0 \Rightarrow \frac{c}{a} <0 \Rightarrow x_1 \cdot x_2 < 0 $$
Pertanto, le radici sono discordi, hanno segno opposto
- x1 >0, x2 <0
- x1 <0, x2 >0
Per la regola della somma, sapendo che a>0 e b>0, deduco che la somma x1+x2<0 è negativa
$$ a>0,b>0 \Rightarrow - \frac{b}{a} < 0 \Rightarrow x_1 + x_2 < 0 $$
Pertanto, la radice positiva è minore in valore assoluto della radice negativa.
- x1 >0, x2 <0 se |x1|<|x2|
- x1 <0, x2 >0 se |x2|<|x1|
F] Una permanenza e una variazione di segno --+
Nel caso di una permanenza iniziale di segno seguita da una variazione (--+) i coefficienti dell'equazione ax2+bx+c=0 sono a<0, b<0 e c>0
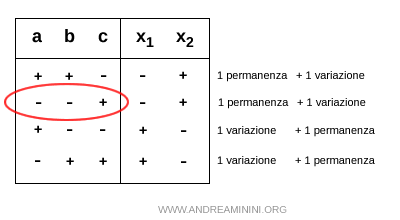
Per la regola del prodotto, sapendo che a<0, c>0 il prodotto x1·x2<0 è negativo
$$ a<0,c>0 \Rightarrow \frac{c}{a} <0 \Rightarrow x_1 \cdot x_2 < 0 $$
Pertanto, le radici sono discordi, hanno segno opposto
- x1 >0, x2 <0
- x1 <0, x2 >0
Per la regola della somma, sapendo che a<0 e b<0, deduco che la somma x1+x2<0 è negativa
$$ a<0,b<0 \Rightarrow - \frac{b}{a} < 0 \Rightarrow x_1 + x_2 < 0 $$
Pertanto, la radice positiva è minore in valore assoluto della radice negativa.
- x1 >0, x2 <0 se |x1|<|x2|
- x1 <0, x2 >0 se |x2|<|x1|
G] Una variazione e una permanenza di segno +--
Nel caso di una variazione iniziale di segno seguita da una permanenza (+--) i coefficienti dell'equazione ax2+bx+c=0 sono a>0, b<0 e c<0
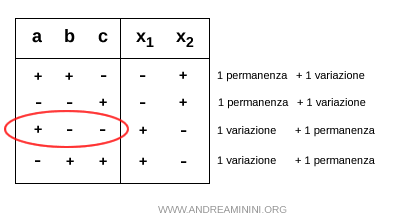
Per la regola del prodotto, sapendo che a>0, c<0 il prodotto x1·x2<0 è negativo
$$ a>0,c<0 \Rightarrow \frac{c}{a} <0 \Rightarrow x_1 \cdot x_2 < 0 $$
Pertanto, le radici sono discordi, hanno segno opposto
- x1 >0, x2 <0
- x1 <0, x2 >0
Per la regola della somma, sapendo che a>0 e b<0, deduco che la somma x1+x2>0 è positiva
$$ a>0,b<0 \Rightarrow - \frac{b}{a} > 0 \Rightarrow x_1 + x_2 > 0 $$
Pertanto, la radice positiva è maggiore in valore assoluto della radice negativa.
- x1 >0, x2 <0 se |x1|>|x2|
- x1 <0, x2 >0 se |x2|>|x1|
H] Una variazione e una permanenza di segno -++
Nel caso di una variazione iniziale di segno seguita da una permanenza (-++) i coefficienti dell'equazione ax2+bx+c=0 sono a<0, b>0 e c>0
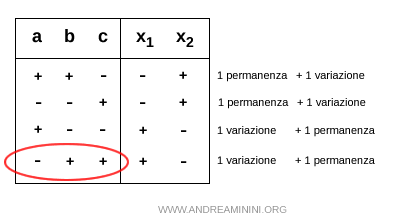
Per la regola del prodotto, sapendo che a<0, c>0 il prodotto x1·x2<0 è negativo
$$ a<0,c>0 \Rightarrow \frac{c}{a} <0 \Rightarrow x_1 \cdot x_2 < 0 $$
Pertanto, le radici sono discordi, hanno segno opposto
- x1 >0, x2 <0
- x1 <0, x2 >0
Per la regola della somma, sapendo che a<0 e b>0, deduco che la somma x1+x2>0 è positiva
$$ a<0,b>0 \Rightarrow - \frac{b}{a} > 0 \Rightarrow x_1 + x_2 > 0 $$
Pertanto, la radice positiva deve essere maggiore in valore assoluto rispetto alla radice negativa.
- x1 >0, x2 <0 se |x1|>|x2|
- x1 <0, x2 >0 se |x2|>|x1|
E così via.
