Le equazioni parametriche
Un'equazione parametrica è un'equazione letterale in cui è presente uno o più lettere dette parametri, diverse dalla variabile incognita, che permettono di rendere vera una condizione.
Quando studio un'equazione parametrica devo considerare i vari valori assegnabili ai parametri.
Se il problema da risolvere fissa una condizione da rispettare, per studiare l'equazione parametrica devo trovare i valori dei parametri che soddisfano la condizione.
Un esempio pratico
Considero l'equazione di 2° parametrica
$$ x^2-2kx+5k-6=0 $$
Dove k è il parametro e x è la variabile incognita.
Devo trovare il valore di k che consente all'equazione di avere due soluzioni reali coincidenti (condizione da soddisfare).
Nota. In questo caso il problema fissa già una condizione da soddisfare. Quindi, devo trovare i valori del parametro che la soddisfano.
Questa condizione implica che il discriminante sia nullo Δ=0.
$$ \Delta = b^2 - 4ac = 0 $$
I coefficienti dell'equazione sono a=1, b=-2k e c=5k-6.
$$ b^2 - 4ac = 0 $$
$$ (-2k)^2 - 4 \cdot (1) \cdot (5k-6) = 0 $$
$$ 4k^2 - 20k + 24 = 0 $$
Quest'ultima è un'equazione di 2° grado
Trovo le soluzioni dell'equazione ossia i valori k che soddisfano l'equazione
$$ k = \frac{-b \pm \sqrt{b^2-4ac}}{2a} $$
In questo caso i coefficienti sono a=4, b=-20 e c=24
$$ k = \frac{-(-20) \pm \sqrt{(-20)^2-4 \cdot 4 \cdot 24}}{2 \cdot 4} $$
$$ k = \frac{20 \pm \sqrt{400 -384}}{8} $$
$$ k = \frac{20 \pm \sqrt{16}}{8} $$
$$ k = \frac{20 \pm 4}{8} $$
$$ k = \begin{cases} \frac{20 - 4}{8} = \frac{16}{8} = 2 \\ \\ \frac{20 + 4}{8} = \frac{24}{8} = 3 \end{cases} $$
Pertanto, quando k=2 v k=3 il discriminante Δ=0 è nullo l'equazione iniziale x2-2kx+5k-6=0 ha due soluzioni reali coincidenti.
Esempio 2
Considero la stessa equazione di 2° grado dell'esempio precedente ma con una condizione diversa
$$ x^2-2kx+5k-6=0 $$
In questo caso devo trovare i valori del parametro k che rendono impossibile l'equazione ossia senza soluzioni reali.
Un'equazione di 2° grado non ha soluzioni reali quando il discriminante è negativo Δ<0.
$$ \Delta = b^2 - 4ac < 0 $$
I coefficienti dell'equazione sono a=1, b=-2k e c=5k-6.
$$ b^2 - 4ac < 0 $$
$$ (-2k)^2 - 4 \cdot (1) \cdot (5k-6) < 0 $$
$$ 4k^2 - 20k + 24 < 0 $$
Per risolvere la disequazione trovo le radici dell'equazione associata
$$ 4k^2 - 20k + 24 = 0 $$
Quest'ultima è un'equazione di 2° grado dove k è l'incognita.
Conosco già le radici k=2 v k=3 avendole calcolate nell'esempio precedente
$$ k = \begin{cases} \frac{20 - 4}{8} = \frac{16}{8} = 2 \\ \\ \frac{20 + 4}{8} = \frac{24}{8} = 3 \end{cases} $$
Il primo coefficiente dell'equazione a>0 è positivo, quindi la parabola ha la concavità rivolta verso l'alto.
Ne consegue che l'equazione 4k2-20k+24=0 assume valori negativi quando k è compreso nell'intervallo (2;3)
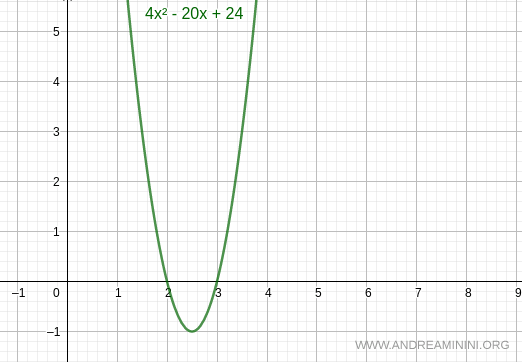
Pertanto, nell'intervallo (2;3) il discriminante Δ<0 è negativo e l'equazione iniziale x2-2kx+5k-6=0 non ha soluzioni reali.
Nota. A questo punto posso dedurre per completezza che negli intervalli esterni (-∞;2)∪(3;∞) il discriminante Δ>0 è positivo e l'equazione iniziale x2-2kx+5k-6=0 ha due soluzioni reali distinte.
E così via.
