Equazioni logaritmiche

Un'equazione logaritmica è un'equazione in cui l'incognita compare nell'argomento di almeno un logaritmo. $$ \log_b P(x) = \log_b Q(x) $$ Dove P e Q sono due polinomi o funzioni dell'incognita x

Per cercare le soluzioni di un'equazione logaritmica posso usare due metodi alternativi

Metodo 1

1. calcolo le condizioni di esistenza dei logaritmi
2. trovo le soluzioni dell'equazione tra gli argomenti P(x)=Q(x)
3. elimino le soluzioni che non rispettano le condizioni di esistenza

Metodo 2

1. assegno il logaritmo a una variabile ausiliaria u=log(x)
2. trovo le soluzioni s dell'equazione rispetto alla variabile ausiliaria u
3. risolvo le equazioni logaritmiche \log(x)=s
4. elimino le soluzioni che non rispettano le condizioni di esistenza

Attenzione. Questa equazione è logaritmica perché l'incognita compare nell'argomento del logaritmo $$ 3 \log(x) = 2 $$ Quest'altra equazione, invece, non è logaritmica perché l'incognita non compare nell'argomento di un logaritmo. $$ (x-1) \log(3) = 5 $$

Un esempio pratico

Devo risolvere l'equazione logaritmica

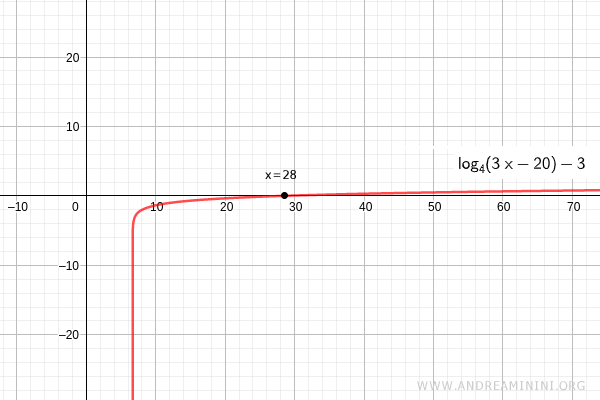
$$\log_4 (3x-20) = 3 $$

Studio le condizioni di esistenza dei logaritmi ponendo gli argomenti maggiori di zero

$$ 3x - 20 > 0 $$

pertanto, l'incognita x deve essere

$$ x > \frac{20}{3} $$

Calcolo l'esponenziale di base 4 in entrambi i membri dell'equazione logaritmica

$$ 4^{\log_4 (3x-20)} = 4^3 $$

$$ 4^{\log_4 (3x-20)} = 64 $$

L'esponenziale e il logaritmo si semplificano

$$ 3x-20 = 64 $$

$$ 3x = 64 + 20 $$

$$ x = \frac{84}{3} $$

Quindi una soluzione è

$$ x = 28 $$

Questa soluzione accettabile come soluzione dell'equazione logaritmica perché x=28 rispetta la condizione di esistenza x>20/3

Esempio 2

Provo a risolvere questa equazione logaritmica usando il metodo della variabile ausiliaria

$$\log_2 x^2 + \log^2_2 x = 0 $$

Riscrivo l'equazione logaritmica in quest'altra forma più leggibile

$$\log_2 x^2 + ( \log_2 x )^2 = 0 $$

La condizione di esistenza dell'equazione logaritmica è x>0

$$ \begin{cases} x^2 > 0 \\ \\ x >0 \end{cases} \Rightarrow x > 0 $$

Per applicare il metodo della variabile ausiliaria i logaritmi devono avere la stessa base e lo stesso argomento

Applico la proprietà del logaritmo di una potenza per far uscire l'esponente di x²

$$ 2 \cdot \log_2 x + ( \log_2 x )^2 = 0 $$

Ora i logaritmi hanno la stessa base e lo stesso argomento

Introduco nell'equazione la variabile ausiliaria u=log₂ x

$$ 2 \cdot u + u^2 = 0 $$

In questo modo riconduco il problema a un'equazione di secondo grado

$$ u \cdot ( u + 2 ) = 0 $$

Questa equazione ha due soluzioni u=0 e u=-2

$$ u = \begin{cases} 0 \\ \\ -2 \end{cases} $$

Sostituisco u con log₂ x

$$ \log_2 x = \begin{cases} 0 \\ \\ -2 \end{cases} $$

Poi verifico se le due equazioni logaritmiche hanno una soluzione

La prima equazione si risolve con x₁=2⁰=1

$$ \log_2x = 0 \Rightarrow 2^0 = 1 $$

La soluzione x₁=1 è accettabile anche per l'equazione logaritmica iniziale perché rispetta le condizioni di esistenza x>0

La seconda equazione si risolve con x₂=2^-2=1/2²=1/4

$$ \log_2x = -2 \Rightarrow 2^{-2} = \frac{1}{4}$$

La soluzione x₂=1/4 è accettabile anche per l'equazione logaritmica iniziale perché rispetta le condizioni di esistenza x>0

Pertanto, le soluzioni dell'equazione logaritmica sono x₁=1 e x₂=1/4

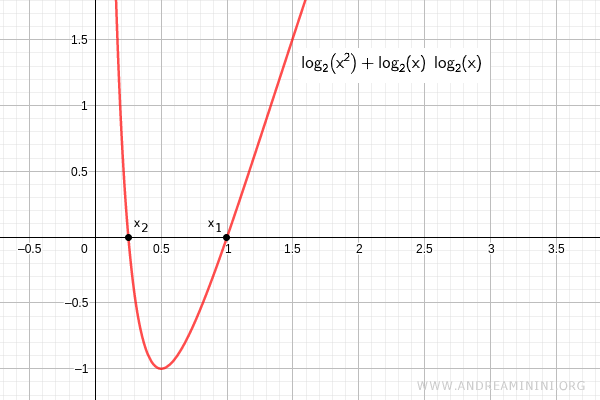
Dimostrazione e spiegazione

I logaritmi sono definiti quando l'argomento è positivo.

$$ P(x) > 0 $$

$$ Q(x) > 0 $$

E' una condizione di esistenza del logaritmo.

Pertanto, l'equazione logaritmica ammette soluzioni solo se sono rispettate le sue condizioni di esistenza.

Per risolvere un'equazione logaritmica basta ricordarsi questa equivalenza

$$ P(x) = Q(x) \Leftrightarrow \log_b P(x) = \log_b Q(x) $$

Spiegazione. Per la proprietà invariantiva di un'equazione posso calcolare l'esponenziale di entrambi i membri. $$ \log_b P(x) = \log_b Q(x) $$ $$ b^{\log_b P(x) } = b^{ \log_b Q(x) } $$ L'esponenziale è l'operazione inversa del logaritmo, quindi l'equazione si semplifica nell'identità degli argomenti. $$ P(x) = Q(x) $$

Pertanto, per trovare le soluzioni dell'equazione logaritmica bisogna cercare le soluzioni dell'equazione tra gli argomenti

$$ P(x) = Q(x) $$

Una volta trovate le soluzioni, vanno eliminare quelle che non rispettano la condizione di esistenza dei logaritmi.

E così via.