L'operatore di parità

L'operatore di parità è l’operatore che descrive matematicamente la riflessione spaziale, cioè l’operazione che inverte le coordinate spaziali di un sistema rispetto all’origine.

In altre parole, applicare la parità significa passare da un sistema a quello “specchiato”, ossia invertire lo spazio.

Ad esempio, se un punto dello spazio ha coordinate

$$ x = (x, y, z) $$

allora l'operatore di parità $ P $ lo trasforma in

$$ P(x) = (-x, -y, -z) $$

Questa trasformazione è detta inversione spaziale.

Applicare l’operatore di parità a un sistema fisico equivale a guardarlo allo specchio, ma non rispetto a un piano: rispetto all’origine.

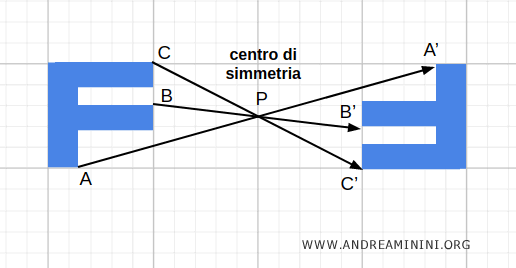
Dal punto di vista geometrico è una simmetria centrale. È una trasformazione globale che inverte destra e sinistra, avanti e indietro, sopra e sotto.

A cosa serve?

L'operatore di parità è molto importante in fisica perché la parità viene conservata in alcune interazioni fondamentali ma non in tutte.

• Se un fenomeno fisico rimane invariato sotto questa trasformazione, si dice che conserva la parità.
• Se invece cambia, allora la parità è violata.

Quindi l'operatore di parità permette di classificare le particelle.

Nota. Nelle interazioni elettromagnetiche e forti, la parità è conservata. Nelle interazioni deboli, invece, la parità è violata, in questo caso la natura distingue tra destra e sinistra. È proprio per questo che esistono neutrini solo sinistrorsi e antineutrini destrorsi. La violazione della parità rivela una delle più profonde asimmetrie della natura.

Le proprietà fondamentali

L'operatore di parità ha alcune proprietà interessanti

Se lo applico due volte, l'operatore parità riporta alla situazione iniziale

$$ P^2 = I $$

Dove $ I $ è l’identità.

Esempio. Considero un punto nello spazio con coordinate: \[ \vec r = (2,-1,3) \] L’operatore di parità inverte tutte le coordinate:
\[ P(\vec r) = (-2,1,-3) \] È come guardare il punto allo specchio passando per l’origine. Ora applico di nuovo l’operatore di parità: \[ P(P(\vec r)) = P(-2,1,-3) = (2,-1,3) \] Si torna al punto iniziale cioè \( P^2 = I \). \[ P^2(\vec r) = \vec r \]

Dal punto di vista fisico questo significa che fare una riflessione spaziale due volte equivale a non fare nulla. Si torna alla configurazione iniziale.

Per questo l’operatore di parità $ P $ ha solo due autovalori possibili: +1 e -1.

• +1 indica uno stato pari
• -1 indica uno stato dispari

Vettori ordinari e pseudovettori

L'operatore di parità mi permette di distinguere le grandezze vettoriali in vettori ordinari e pseudovettori.

• Vettori ordinari
  Un vettore ordinario (o vettore polare), come posizione, velocità o forza, cambia segno dopo l'inversione spaziale: $$ P( \vec{v} ) = - \vec{v} $$
• Pseudovettori
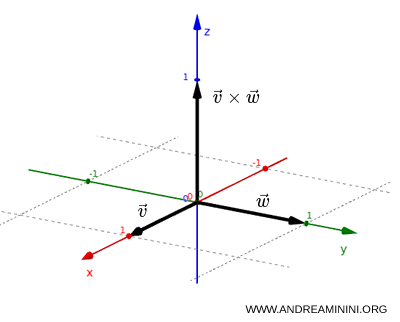
  Uno pseudovettore (o vettore assiale), come il momento angolare o il campo magnetico, non cambia segno dopo l'inversione spaziale. $$ P(\vec v \times \vec w) = (-\vec v) \times (-\vec w) = \vec v \times \vec w = \vec L $$

  Dimostrazione. Se \( \vec L = \vec v \times \vec w \) con \( \vec v \) e \( \vec w \) vettori polari, allora sotto l’azione dell’operatore di parità \( P \) si ha $$ P(\vec v) = -\vec v, \quad P(\vec w) = -\vec w $$ e quindi  $$ P(\vec L) = \vec L $$Esempio. Considero due vettori nel piano: $$  \vec v = (1,0) \qquad \vec w = (0,1) $$ Il prodotto vettoriale è un vettore uscente dal piano (asse ( z ) $$ \vec v \times \vec w = (0,0,1) $$ Questo vettore è perpendicolare al piano ed è uno pseudovettore. Infatti, se applico l’inversione spaziale ottengo $ (x,y) \rightarrow (-x,-y) $ e quindi: $$ P(\vec v) = (-1,0), \quad P(\vec w) = (0,-1) $$ Ora rifaccio il prodotto vettoriale: $$ P(\vec v) \times P(\vec w) = (-1,0) \times (0,-1) = (0,0,1) $$  Il risultato è lo stesso $$ P(\vec v \times \vec w) = \vec v \times \vec w $$ Il verso non cambia. Quindi, dal punto di vista fisico, l’inversione spaziale ribalta le direzioni ma non il verso di una rotazione.
  

Scalare e pseudoscalare

L'operatore di parità mi permette anche di distinguere le grandezze numeriche in scalari e pseudoscalari.

• Scalare
  Uno grandezza numerica è detta scalare se non cambia segno dopo l'inversione spaziale.

  Esempio. La temperatura in un punto è \( T = 20^\circ \text{C} \).  Se applico l’inversione spaziale, la temperatura non cambia. $$  P(T) = T $$ La temperatura non ha direzione, non dipende dall’orientazione dello spazio. Ha lo stesso valore e segno anche allo "specchio". Quindi, è una grandezza scalare.

• Pseudoscalare
  Una grandezza numerica è detta pseudoscalare se cambia segno dopo l'inversione spaziale.

  Esempio. Considero tre vettori \[ \vec a = (1,0,0) \\ \vec b = (0,1,0) \\ \vec c = (0,0,1) \] Poi calcolo il prodotto scalare triplo: \[ S = \vec a \cdot (\vec b \times \vec c) \] Sapendo che \( \vec b \times \vec c = (1,0,0) \) ottengo: \[
  S = \vec a \cdot (\vec b \times \vec c) = 1 \] Ora applico la parità: \[ P(\vec a) = (-1,0,0) \\ P(\vec b) = (0,-1,0) \\ P(\vec c) = (0,0,-1) \] Calcolo di nuovo: \[ P(S) = P( \vec a ) \cdot ( P( \vec b ) \times P( \vec c ) )  \] \[ P(S) = (-1,0,0) \cdot ( (0,-1,0) ) \times (0,0,-1) )  \] Poiché \( (0,-1,0) \times (0,0,-1) = (1,0,0) \)  ottengo: \[ P(S) = (-1,0,0) \cdot ( \underbrace{ (0,-1,0) ) \times (0,0,-1) }_{(1,0,0)} )  \] \[ P(S) = (-1,0,0) \cdot (1,0,0) = -1 \] Il risultato finale cambia segno (-1). Questo è un esempio di grandezza pseudoscalare.

Gli autovalori degli scalari, pseudoscalari, vettori, pseudovettori

L’operatore di parità \( P \) agisce sulle grandezze fisiche assegnando a ciascuna un autovalore che può assumere esclusivamente i valori +1 oppure -1.

Gli scalari risultano invarianti sotto inversione spaziale e sono quindi caratterizzati dall’autovalore +1.  I pseudoscalari, al contrario, cambiano segno quando si applica la trasformazione di parità e possiedono autovalore -1.

Grandezza	Trasformazione di parità	Autovalore
Scalare	\( P(s)=s \)	\( +1 \)
Pseudoscalare	\( P(p)=-p \)	\( -1 \)
Vettore (o vettore polare)	\( P(\vec v)=-\vec v \)	\( -1 \)
Pseudovettore (o vettore assiale)	\( P(\vec a)=\vec a \)	\( +1 \)

Un comportamento analogo si osserva per i vettori ordinari (o vettori polari), come lo spostamento o la velocità, che sotto l’azione della parità invertono il verso e sono pertanto associati all’autovalore -1.

Viceversa, i pseudovettori (o vettori assiali), come il momento angolare, restano invariati sotto inversione spaziale e sono quindi descritti dall’autovalore +1.

Riepilogando, gli scalari e gli pseudovettori non cambiano dopo un'inversione spaziale, ossia dopo una trasformazione di parità.

La parità nelle particelle

La parità è un numero quantico delle particelle, al pari dello spin, della carica elettrica, dell’isospin, della stranezza e così via. 

Descrive il comportamento dello stato quantistico di una particella sotto inversione spaziale.

Esistono alcune differenze fondamentali tra le principali famiglie di particelle.

• Nei fermioni (particelle con spin semi-intero), la parità di una particella è opposta a quella della corrispondente antiparticella.
• Nei bosoni (particelle con spin intero), invece, una particella e la sua antiparticella hanno la stessa parità.

Nelle particelle composte, la parità totale si ottiene come prodotto delle parità dei costituenti. La parità è quindi un numero quantico moltiplicativo. Questo la distingue da numeri quantici come la carica elettrica o la stranezza, che sono additivi.

Adroni

Poiché le interazioni forti conservano la parità, gli adroni (barioni e mesoni) sono autostati dell’operatore di parità e possono essere classificati in base al valore:

$$ p = \pm 1 $$

Barioni

Per convenzione si assegna ai quark una parità intrinseca positiva:

$$ p(quark) = +1 $$

Di conseguenza, un barione composto da tre quark ha parità:

$$ p = (+1)^3 = +1 $$

Pertanto, i barioni nello stato fondamentale hanno parità positiva.

Mesoni

I mesoni sono composti da un quark e un antiquark. Poiché l’antiquark ha parità opposta rispetto al quark, la parità del mesone nello stato fondamentale è -1:

$$ p = (+1) \cdot (-1) = -1 $$

Per mesoni in uno stato eccitato, compare anche il contributo del momento angolare orbitale l. In questo caso la parità è:

$$ p = (-1)^{l+1} $$

Dove $ l $ è il momento angolare orbitale del moto relativo quark - antiquark.

Fotone

Il fotone è una particella vettoriale con spin 1 ed è associato al potenziale vettore elettromagnetico. La sua parità intrinseca è -1:

$$ p = -1 $$

Per il fotone, la parità intrinseca non è direttamente osservabile come per le particelle massive, ma è definita attraverso il comportamento del campo elettromagnetico sotto inversione spaziale.

E così via.