L’isospin e la simmetria SU(2) dei quark up e down
Si parla di simmetria tra i quark up (u) e down (d) perché, nelle interazioni forti, essi hanno masse molto simili, rispondono alla forza forte nello stesso modo e possono trasformarsi l’uno nell’altro senza modificare la teoria. In altre parole, scambiando un quark up con un quark down, la forza forte rimane invariata.
Per rappresentare l'invarianza della forza forte sotto trasformazioni che mescolano i quark up e down si introduce l’isospin.
L’isospin non è uno spin ma obbedisce alla stessa algebra dello spin:
- Lo spin riguarda lo spazio fisico e descrive come cambia una particella quando la ruoti realmente nello spazio. E' una rotazione "fisica" della particella nello spazio.
- L'isospin riguarda uno spazio interno, non fisico, in cui i quark up e down sono trattati come due componenti di uno stesso "vettore" nello spazio di isospin. Quindi, è una rotazione del vettore (u,d) che descrive lo scambio tra i quark up e down. Non è una rotazione fisica.
Matematicamente le due simmetrie usano lo stesso gruppo $ SU(2) $, quindi le equazioni hanno la stessa forma, ma descrivono un fenomeno diverso.
Nel caso dell'isospin si parla di simmetria interna perché non ha nulla a che fare con lo spazio.
Nota. Si usa l'isospin perché permette di descrivere in modo compatto e matematicamente preciso tutte le trasformazioni che mescolano i quark up e down senza alterare la forza forte. In questo modo, proprietà e reazioni che sembrano diverse diventano manifestazioni di una stessa simmetria interna. Ad esempio, l’isospin spiega perché particelle con cariche diverse possono avere masse quasi identiche, perché alcune reazioni forti hanno probabilità uguali e perché certi decadimenti sono proibiti quando violano la simmetria. Sono tutte conseguenze fisiche della simmetria.
Quindi, l'isospin non è un vettore nello spazio con componenti lungo le direzioni $ x, y, z $ ma un vettore con tre componenti astratte $ I_1 $, $ I_2 $, $ I_3 $
Per questa ragione, quando parliamo di isospin si usano due numeri:
- $ I $ è il il valore totale dell’isospin
dice quanti stati ha la particella - $ I_3 $ è la componente dell’isospin
dice quale di quegli stati si sta osservando
Se la forza forte è invariante rispetto alle rotazioni nello spazio $ SU(2) $ dell’isospin, allora, per il teorema di Noether, l’isospin deve conservarsi in ogni processo governato dall'interazione forte.
Nota. È lo stesso principio per cui il momento angolare si conserva in tutti i fenomeni che rispettano l’invarianza rotazionale nello spazio fisico.
L’invarianza $ SU(2) $ comporta che gli stati si organizzino in multiplette ben definite:
- doppietti con $ I = \frac{1}{2} $
- triplette con $ I = 1 $
- quartetti con $ I = \frac{3}{2} $
A ciascuno di questi multipletti si assegna un particolare isospin $ I $ e a ogni componente del multipletto un particolare $ I_3 $.
Per determinare l’isospin \( I \) di un multipletto è sufficiente contare il numero degli stati con valori diversi di \( I_3 \).
Poiché \( I_3 \) varia da \( -I \) a \( +I \) in passi interi, ogni multipletto contiene \( 2I + 1 \) stati.
Questa struttura a multiplette è una conseguenza diretta della simmetria.
Esempio. I pioni $ \pi $ si presentano in tre stati: $ \pi^+ $, $ \pi^0$, $ pi^- $
$$ 2I+1 = 3 $$
Quindi, l'isospin totale del pione è:
$$ I = \frac{3-1}{2} = \frac{2}{2} = 1 $$
Le tre componenti del pione $ \pi $ corrispondono ai valori di $ I_3 $:
- $ \pi^+ $ con $ I_3 = 1 $
- $ \pi^0 $ con $ I_3 = 0 $
- $ \pi^- $ con $ I_3 = -1 $
Espresse come ket di isospin:
$$ \pi^+ = |1,1 > $$
$$ \pi^0 = |1,0 > $$
$$ \pi^- = |1,-1 > $$
L'origine dell'isospin
L'isospin venne introdotto da Werner Heisenberg nel 1932.
Fu lui a rendersi conto che protone e neutrone avevano masse quasi identiche, interagivano allo stesso modo tramite la forza forte.
Per spiegare questa somiglianza propose una nuova quantità quantistica, costruita sulla stessa matematica dello spin, ma applicata alla struttura interna dei nucleoni anziché allo spazio fisico. Così nacque il concetto di isotopic spin, abbreviato poi in isospin.
Secondo Heisenberg il protone e il neutrone erano due stati diversi della stessa particella, il nucleone $ N $.
$$ N = \frac{ \alpha }{ \beta } $$
Dove il protone ( p ) e il neutrone ( n ) sono i due stati nel nucleone.
$$ p = \frac{1}{0} $$
$$ n = \frac{0}{1} $$
Il nucleone ha come spin totale $ \frac{1}{2} $La geometria
$$ I = \frac{1}{2} $$
La componente $ I_3 $, invece, ha come autovettore $ I_3 = + \frac{1}{2} $ nel protone e $ I_3 = - \frac{1}{2} $ nel neutrone.
$$ p = | \frac{1}{2} , + \frac{1}{2} >$$
$$ n = | \frac{1}{2} , - \frac{1}{2} >$$
In questo modo il protone e il neutrone sono trattati come due stati della stessa particella (il nucleone) analoghi allo spin-up e spin-down. La grandezza che li distingue è l’isospin.
Una rotazione di 180° attorno all’asse nello spazio dell’isospin trasforma i protoni in neutroni, e viceversa.
L’isospin si applica anche ai diversi sapori dei quark.
In particolare, i quark up ( u ) e down (d) formano un doppietto di isospin, esattamente come protone e neutrone.
$$ u = | \frac{1}{2} , + \frac{1}{2}> $$
$$ d = | \frac{1}{2} , - \frac{1}{2}> $$
Entrambi hanno ispospin $ I = \frac{1}{2} $ mentre differiscono per il valore della componente $ I_3 $:
- il quark up ha $ I_3= +\frac{1}{2} $
- il quark down ha $ I_3 = - \frac{1}{2} $
Tutti gli altri sapori dei quark ( s, c, b, t ) hanno isospin zero.
La combinazione di due nucleoni
L’isospin non serve solo a classificare le particelle, influisce anche su quali stati sono fisicamente possibili.
Dal momento che protoni e neutroni sono due stati di un doppietto con \( I = \tfrac12 \), quando combino due nucleoni, la regola di addizione dei momenti angolari dà:
$$ \tfrac12 \otimes \tfrac12 = 1 \oplus 0 $$
Nota. Vediamo come si calcola l'addizione di due isospin \( \tfrac12 \)$$ I_1 = \tfrac12 \\ I_2 = \tfrac12 $$ I valori possibili dell’isospin totale \( I \) sono dati dalla regola generale dell’addizione dei momenti angolari: $$ I = |I_1 - I_2|,\ |I_1 - I_2|+1,\ \dots,\ I_1 + I_2 $$ In questo caso $$ I = |\tfrac12 - \tfrac12| = 0 $$ $$ I = \tfrac12 + \tfrac12 = 1 $$ Quindi i due valori possibili sono: $$ I = 1 \quad (\text{tripletto}) $$ $$ I = 0 \quad (\text{singoletto}) $$ Ed è esattamente questo che sintetizza la notazione $$ \tfrac12 \otimes \tfrac12 = 1 \oplus 0 $$
Questo significa che determina:
- un tripletto simmetrico con isospin \( I = 1 \) $$ |1,1\rangle = |pp\rangle \\ |1,0\rangle = \frac{1}{\sqrt{2}} ( |pn\rangle + |np\rangle ) \\ |1,-1\rangle = |nn\rangle $$
- un singoletto antisimmetrico con isospin \( I = 0 \) $$ |0,0\rangle = \frac{1}{\sqrt{2}} ( |pn\rangle - |np\rangle ) $$
Queste sono le uniche combinazioni possibili.
Quale di questi stati esiste realmente in natura?
Sperimentalmente, esiste un solo stato legato di due nucleoni: il deuterone (pn), composto da un protone e un neutrone.
Invece, non esiste un nucleo stabile formato da due protoni (pp), né un nucleo stabile formato da due neutroni (nn).
Quindi il deuterone non può appartenere al tripletto \( I = 1 \) perché allora esisterebbero necessariamente tutti e tre gli stati: ( pp ), ( pn ), ( nn ) ... ma due di questi non esistono.
La simmetria \( SU(2) \) infatti li collega tramite semplici rotazioni nello spazio dell’isospin.
L’unica possibilità è che il deuterone (pn) sia nel singoletto \( I = 0 \).
Come il doppietto dei quark (u,d) genera tutti i multiplette di isospin
L’isospin dei quark leggeri è
$$ I = \frac{1}{2} $$
e le due componenti sono i quark up (u) e down (d):
$$ u = \left| \frac12, +\frac12 \right> $$
$$ d = \left| \frac12, -\frac12 \right> $$
Questo doppietto (u,d) è la sorgente di tutti i multiplette osservati.
1] Mesoni (q\bar q)
Combinare due isospin \( \frac12 \) dà:
$$ \frac12 \otimes \frac12 = 1 \oplus 0 $$
In altre parole, i mesoni possono presentarsi con un solo stato (singoletto $ I = 0 $) oppure con tre stati (tripletto $ I=1 $). Non esistono altre possibilità.
Esempio 1. Un esempio di tripletto dei pioni ($ I=1 $) sono i pioni $$ \pi^+ = \left| 1, +1 \right> $$ $$ \pi^0 = \left| 1, 0 \right> $$ $$ \pi^- = \left| 1, -1 \right> $$ Esempio 2. L’unico singoletto costruito da \(u\bar u\) e \(d\bar d\) è la combinazione antisimmmetrica, spesso indicata come stato \( \eta_0 \) del settore \((u,d) \).
2] Barioni (qqq)
La combinazione di tre isospin \( \frac12 \) dà la seguente struttura:
$$ \frac12 \otimes \frac12 \otimes \frac12 $$
Sapendo che $ \frac12 \otimes \frac12 = 1 \oplus 0 $
$$ \left(1 \oplus 0\right) \otimes \frac12 $$
Applico la proprietà distributiva
$$ \left(1 \otimes \frac12\right) \oplus \left(0 \otimes \frac12\right) $$
Sapendo che $ 1 \otimes \frac12 = \frac32 \oplus \frac12 $ e $ 0 \otimes \frac12 = \frac12 $
$$ \left(\frac32 \oplus \frac12\right) \oplus \left(\frac12\right) $$
Applico la proprietà associativa
$$ \frac32 \oplus \frac12 \oplus \frac12$$
Quindi, ottengo due doppietti $ I=\frac12 $ e un quartetto $ I = \frac32 $.
In altre parole, i barioni possono presentarsi con due stati (doppietto $ I = \frac12 $) oppure con quattro stati (quartetto $ I=\frac32 $). Non esistono altre possibilità.
Esempio 1. Un esempio di doppietto dei nucleoni $ I = \frac12 $ è il protone, un altro esempio è il neutrone. $$ p = uud = \left| \tfrac12, +\tfrac12 \right> $$ $$ n = udd = \left| \tfrac12, -\tfrac12 \right>$$ Sono gli unici due barioni con isospin (1/2) composti da (u,d).
Esempio 2. Un esempio di quartetto ($ I = \frac32 $) delle particelle è la particella $ \Delta $ $$ \Delta^{++} = uuu = \left| \tfrac32, +\tfrac32 \right> $$ $$ \Delta^{+} = uud = \left| \tfrac32, +\tfrac12 \right>$$ $$ \Delta^{0} = udd = \left| \tfrac32, -\tfrac12 \right> $$ $$ \Delta^{-} = ddd = \left| \tfrac32, -\tfrac32 \right> $$ Questi stati sono completamente simmetrici nel sapore.
L'idea chiave è che gli isomultiplette non sono arbitrarî, bensì sono la conseguenza matematica della simmetria $ SU(2)$.
Se la QCD tratta $ u $ e $ d $ come quasi-identici, allora tutti gli adroni composti solo da (u,d) devono organizzarsi esattamente come le rappresentazioni del gruppo $ SU(2) $.
Un esempio pratico
In questo esempio considero la particella $ \Delta $ che ha quattro stati in natura: $ \Delta^{++}, \Delta^{+}, \Delta^{0}, \Delta^{-} $
$$ 2I + 1 = 4 $$
Pertanto, ha come isospin totale $ I = \frac{3}{2} $
$$ I = \frac{4-1}{2} = \frac{3}{2} $$
Essendo $ I = \frac{3}{2} $ appartiene al quartetto.
Le quattro componenti hanno valori di ( I_3 ):
$$ I_3 = +\frac32,\ +\frac12,\ -\frac12,\ -\frac32 $$
I corrispondenti stati fisici sono:
- \( \Delta^{++} \) con \( I_3 = +\tfrac32 \)
- \( \Delta^{+} \) con \( I_3 = +\tfrac12 \)
- \( \Delta^{0} \) con \( I_3 = -\tfrac12 \)
- \( \Delta^{-} \) con \( I_3 = -\tfrac32 \)
Espressi come ket:
- \( \Delta^{++} = \left| \tfrac32 , +\tfrac32 \right\rangle\)
- \( \Delta^{+} = \left| \tfrac32 , +\tfrac12 \right\rangle \)
- \( \Delta^{0} = \left| \tfrac32 , -\tfrac12 \right\rangle \)
- \( \Delta^{-} = \left| \tfrac32 , -\tfrac32 \right\rangle \)
Dal punto di vista del sapore dei quark, questi stati sono:
- \( \Delta^{++} = uuu \)
- \( \Delta^{+} = uud \)
- \( \Delta^{0} = udd \)
- \( \Delta^{-} = ddd \)
Esempio. La particella \( \Delta^{++} \) appartiene al multipletto con isospin \( I = \tfrac32 \) e ha la componente massima \( I_3 = +\tfrac32 \). Poiché ogni quark up ha \( I_3 = +\tfrac12 \), l’unica combinazione possibile per ottenere \[ I_3 = \frac12 + \frac12 + \frac12 = \frac32 \] è una terna di quark up: \[ \Delta^{++} = uuu \] Questo non determina l’isospin totale \( I = \tfrac32 \), che invece è fissato dalla rappresentazione simmetrica del gruppo \( SU(2) \), ma spiega perché la composizione \( uuu \) realizza la componente massima del multipletto.
In conclusione, il multipletto delle particelle \( \Delta \) ha quattro stati perché deriva direttamente dalla combinazione di tre isospin \( \tfrac12 \):
\[ \frac12 \otimes \frac12 \otimes \frac12 \]
Come mostrato nell’esempio generale sui barioni, ossia di particelle composte da tre quark, il risultato di questo prodotto tensoriale è un quartetto $ \frac32 $ e due doppietti $ \frac12 $.
\[ \frac32 \oplus \frac12 \oplus \frac12 \]
Il termine \( I = \tfrac32 \) rappresenta la rappresentazione massima, quella completamente simmetrica nel sapore.
Questa rappresentazione contiene quattro stati, ciascuno con un diverso valore della componente:
\[ I_3 = +\tfrac32,\ +\tfrac12,\ -\tfrac12,\ -\tfrac32 \]
La rappresentazione \( I = \tfrac32 \) è completamente simmetrica nel sapore e genera esattamente quattro stati, ognuno corrispondente a un diverso valore di \( I_3 \).
\[ \Delta^{++},\ \Delta^{+},\ \Delta^{0},\ \Delta^{-} \]
Questa struttura non è arbitraria, ma è una conseguenza diretta della simmetria \( SU(2) \): se i quark \( u \) e \( d \) formano un doppietto con isospin \( \tfrac12 \), allora tutti gli adroni composti da tre quark devono organizzarsi esattamente nelle rappresentazioni del gruppo, tra cui la rappresentazione massima \( I = \tfrac32 \) che genera il quartetto delle particelle \( \Delta \).
Perché scambiare un quark up e down non cambia la forza forte
Considero il doppietto dei quark:
\[ \begin{pmatrix} u \\ d \end{pmatrix} \]
Ora applico una trasformazione SU(2), che matematicamente è una rotazione in uno spazio astratto:
\[ \begin{pmatrix} u' \\ d' \end{pmatrix} = \begin{pmatrix} \cos\theta & \sin\theta \\ -\sin\theta & \cos\theta \end{pmatrix} \begin{pmatrix} u \\ d \end{pmatrix} \]
Questa trasformazione mescola i quark up (u) e down (d)
- $ u' = \cos\theta \ u + \sin\theta \ d $
- $ d' = -\sin\theta \ u + \cos\theta \ d $
La cosa sorprendente è che la forza forte tratta $ u' $ e $ d' $ nello stesso modo in cui trattava $ u $ e $ d $.
Si parla di simmetria perché i quark $ u $ e $ d $ possono essere mescolati tramite qualsiasi rotazione SU(2) senza modificare la forza forte. [
pp = |1\ 1\rangle ;\longrightarrow; |0\ 0\rangle \otimes |1\ 1\rangle = |1\ 1\rangle
]
Di conseguenza, gli adroni costruiti con $ u′ $ e $ d′ $ hanno le stesse interazioni e le stesse proprietà di quelli costruiti con $ u $ e $ d $. Questo è il significato profondo della simmetria.
In questo modo i quark $ u $ e $ d $ diventano due stati di una stessa entità.
Ad esempio, scambiando un quark $ u $ con un quark $ d $, il protone ($ p = uud $) e il neutrone ($ n = udd $) si trasformano uno nell’altro come un doppietto: \[ \begin{pmatrix} p' \\ n' \end{pmatrix} = \begin{pmatrix} \cos\theta & \sin\theta \\ -\sin\theta & \cos\theta \end{pmatrix} \begin{pmatrix} p \\ n \end{pmatrix} \] La QCD non distingue questa trasformazione. Pertanto, per la forza forte il protone (p) e il neutrone (n) sono equivalenti.
Un esempio pratico
Metto protone e neutrone in un doppietto di isospin
Scrivo il doppietto dei nucleoni come vettore a due componenti nello spazio di isospin:
$$ N = \begin{pmatrix} p \\ n \end{pmatrix} $$
Dove \( p \) è il protone e \( n \) è il neutrone mentre $ N $ è il nucleone, ossia la particella a due stati che comprende il protone e il neutrone.
Queste sono le basi dello spazio a due dimensioni dell’isospin \(I = \tfrac12\).
Effetto una rotazione $ SU(2) $ nello spazio dell’isospin
Prendo una matrice di rotazione SU(2) reale del tipo
\[ R(\theta) = \begin{pmatrix} \cos\theta & \sin\theta \\ -\sin\theta & \cos\theta \end{pmatrix} \]
Questa matrice soddisfa le condizioni di unitarietà e determinante unitario
\[ R^\dagger R = \mathbb{1}, \quad \det R = 1 \]
Dove \( R^\dagger \) è la matrice coniugata trasposta di \( R \).
In altre parole, \( R \) è una matrice unitaria \( 2 \times 2 \) con determinante uguale a 1, quindi è un elemento del gruppo \( SU(2) \).
Applico la rotazione al doppietto:
\[ \begin{pmatrix} p' \\ n' \end{pmatrix} = R(\theta) \begin{pmatrix} p \\ n \end{pmatrix} \]
\[ \begin{pmatrix} p' \\ n' \end{pmatrix} = \begin{pmatrix} \cos\theta & \sin\theta \\ -\sin\theta & \cos\theta \end{pmatrix} \begin{pmatrix} p \\ n \end{pmatrix} \]
Da cui ottengo il sistema di equazioni nella forma generale:
\[ \begin{cases} p' = p \cdot \cos\theta + n \cdot \sin\theta \\ \\ n' = -p \cdot \sin\theta + n \cdot \cos\theta \end{cases} \]
A questo punto scelgo un angolo specifico di rotazione. Ad esempio, una rotazione con \( \theta = \frac{\pi}{2} \) ossia di 90 gradi.
\[ \begin{cases} p' = p \cdot \cos \frac{\pi}{2} + n \cdot \sin \frac{\pi}{2} \\ \\ n' = -p \cdot \sin \frac{\pi}{2} + n \cdot \cos \frac{\pi}{2} \end{cases} \]
Sapendo che \( \cos \frac{\pi}{2} = 0 \) e \( \sin \frac{\pi}{2} = 1 \)
\[ \begin{cases} p' = p \cdot 0 + n \cdot 1 \\ \\ n' = -p \cdot 1 + n \cdot 0 \end{cases} \]
\[ \begin{cases} p' = n \\ \\ n' = -p \end{cases} \]
Quindi, con una rotazione di \( 90^\circ \) nello spazio di isospin ottengo \( p' = n \) e \( n' = -p \).
Il segno meno davanti a \( p \) è solo una fase globale di \( \pi \) cioè un fattore \( e^{i\pi} = -1) \). Dal punto di vista fisico una fase globale non ha effetto osservabile, quindi lo stato \( n' = -p \) è fisicamente equivalente a \( p \).
In conclusione, la rotazione \( SU(2) \) di \( \theta = \frac{\pi}{2} \) scambia "matematicamente" protone e neutrone.
\[ R\left(\frac{\pi}{2}\right) \begin{pmatrix} p \\ n \end{pmatrix} = \begin{pmatrix} n \\ -p \end{pmatrix} \]
In altre parole, protone e neutrone sono due componenti di un vettore che può essere ruotato in uno spazio a due dimensioni, esattamente come un vettore nello spazio ordinario.
Nota. Fisicamente questa rotazione non è vera una rotazione nello spazio reale, ma una rotazione nello spazio interno dell’isospin. La simmetria dice solo che la forza forte è invariante sotto queste rotazioni, cioè non “vede” la differenza tra i vari punti di questo spazio, quindi non distingue protoni e neutroni nelle interazioni forti.
Isospin e trasformazioni tra nucleoni
L’isospin non descrive solo gli stati legati, ma anche le trasformazioni tra protoni, neutroni e pioni che avvengono nelle collisioni e che rispettano le simmetrie dell’interazione forte.
Esempio
Considero questa reazione di scattering in cui due protoni $(p)$ si scontrano formando un deuterone ($ d $) e un pione ($ \pi $):
$$ p + p \rightarrow d + \pi^{+} $$
All’inizio i due protoni hanno isospin totale \( I = 1 \) e proiezione \( I_3 = +1 \), perché ciascun protone contribuisce con \( +\tfrac{1}{2} \).
$$ I = \frac12 + \frac12 = 1 $$
$$ I_3 = \frac12 + \frac12 = 1 $$
Nota. Sia il protone che il neutrone formano un doppietto di isospin con valore totale \( I = \tfrac{1}{2} \). Il protone ha proiezione \( I_3 = +\tfrac{1}{2} \), mentre il neutrone ha \( I_3 = -\tfrac{1}{2} \). I pioni, invece, formano un tripletto con isospin totale \( I = 1 \): il pione \( \pi^{+} \) ha \( I_3 = +1 \), il pione \( \pi^{0} \) ha \( I_3 = 0 \) e il pione \( \pi^{-} \) ha \( I_3 = -1 \).
Poiché \( p + p \) non si legano mentre \( p + n \) sì, per formare il deuterone ($ d $) deve necessariamente avvenire una trasformazione: uno dei due protoni \( p \) deve convertirsi in un neutrone \( n \).
Il passaggio da \( I_3 = +\tfrac12 \) (protone) a \( I_3 = -\tfrac12 \) (neutrone) avviene tramite l’emissione del pione \( \pi^{+} \):
$$ p + p \rightarrow p + n + \pi^+ $$
Alla fine compare un deuterone \( d \), formato da un protone e un neutrone \((d = p + n) \), che ha isospin \( I = 0 \) e proiezione \( I_3 = \tfrac12 - \tfrac12 = 0 \), e un pione \( \pi^{+} \) che ha \( I = 1 \) e \( I_3 = +1 \)
$$ p + p \rightarrow d + \pi^+ $$
La proiezione \( I_3 \) si conserva perfettamente, poiché il valore iniziale \( +1 \) si ritrova nel pione finale.
$$ \underbrace{p + p}_{I_3 = \frac12+ \frac12 = +1} \rightarrow \underbrace{ d + \pi^{+} }_{I_3 = 0+1 = +1} $$
Nota. La proiezione \( I_3 \) si conserva sempre nelle interazioni forti, perché è direttamente legata alla carica elettrica. L’isospin totale \( I \), invece, non è garantito che rimanga invariato, poiché può modificarsi quando entrano in gioco effetti che rompono la simmetria di isospin, come i contributi elettromagnetici o le differenze di massa tra protone e neutrone.
Nella notazione a ket di Dirac, sapendo che ogni protone è $ p = | \frac12 \ + \frac12 \rangle $, si può anche scrivere
\[ pp = |1\ 1\rangle \longrightarrow |0\ 0\rangle \otimes |1\ 1\rangle = |1\ 1\rangle \]
A sinistra c'è $ pp = |1 \ 1 \rangle $, a destra $ |1 \ 1 \rangle $, quindi la simmetria di isospin è rispettata.
Come si calcola $ |0\ 0\rangle \otimes |1\ 1\rangle $? Per fare il calcolo devo considerare separatamente l'isospin $ I $ e la proiezione $ I_3 $. Un sistema composto da due oggetti con isospin \( I_1 \) e \( I_2 \), l’isospin totale può assumere i valori: \[ I = |I_1 - I_2|, |I_1 - I_2|+1, \ldots , I_1 + I_2 \] In questo caso, il deuterone ha isospin \( I_1 = 0 \) e il pione ha isospin \( I_2 = 1 \) Quindi i possibili valori dell’isospin totale sono: \[ I = |0 - 1| = 1 \quad \text{fino a} \quad 0 + 1 = 1 \] Cioè c’è un solo valore possibile \[ I = 1 \] Il valore di \( I_3 \) si somma sempre. In questo caso il deuterone ha \( I_{3,d} = 0 \) e il pione \( \pi^+ \) ha \( I_{3,\pi} = +1 \) Quindi: \[ I_3 = 0 + 1 = +1 \] Pertanto, il prodotto tensoriale è \[ |0\ 0\rangle \otimes |1\ 1\rangle = |1\ 1\rangle \]
Esempio 2
Considero ora la reazione in cui un protone \( p \) e un neutrone \( n \) si scontrano formando un deuterone \( d \) e un pione neutro:
\[ p + n \rightarrow d + \pi^{0} \]
All’inizio il protone ha proiezione \( I_3 = +\tfrac12 \) e il neutrone ha \( I_3 = -\tfrac12 \). La loro somma è dunque nulla:
\[ I_3 = \tfrac12 - \tfrac12 = 0 \]
L’isospin totale \( I \) del sistema \( p + n \) può assumere due valori, 0 oppure 1, perché l’addizione di due isospin \( \tfrac12 \) genera sia un singoletto sia un tripletto. Nel caso del deuterone, però, so già che lo stato legato corrisponde al canale \( I = 0 \).
Alla fine della reazione compare quindi un deuterone \( d \) con isospin \( I = 0 \) e proiezione \( I_3 = 0 \), insieme a un pione neutro \( \pi^{0} \), che ha isospin \( I = 1 \) e proiezione \( I_3 = 0 \):
\[ p + n \rightarrow d + \pi^{0} \]
La proiezione \( I_3 \) si conserva perfettamente, poiché il valore iniziale 0 si ritrova nella somma delle proiezioni finali:
\[ \underbrace{p + n}_{I_3 = \tfrac12 - \tfrac12 = 0} \longrightarrow \underbrace{d + \pi^{0}}_{I_3 = 0 + 0 = 0} \]
In questo caso non è necessaria alcuna trasformazione di particelle, perché la coppia protone - neutrone è già quella che può legarsi formando il deuterone.
Nella notazione a ket di Dirac sapendo che ogni neutrone è $ n = | \frac12 \ - \frac12 \rangle $ e ogni protone è $ p = | \frac12 \ + \frac12 \rangle $, si scrive
\[ pn = |1\ 0\rangle \longrightarrow |0\ 0\rangle \otimes |1\ 0\rangle = |1\ 0\rangle \]
A sinistra c’è \( pn = |1\ 0\rangle \), a destra c’è di nuovo \( |1\ 0\rangle \), quindi la simmetria di isospin è rispettata.
Esempio 3
Considero ora la reazione in cui due neutroni \( n \) si scontrano formando un deuterone \( d \) e un pione negativo:
\[ n + n \rightarrow d + \pi^{-} \]
Il neutrone ha proiezione \( I_3 = -\tfrac12 \). La proiezione totale iniziale vale quindi:
\[ I_3 = -\tfrac12 - \tfrac12 = -1 \]
Poiché due neutroni non formano uno stato legato, non possono generare direttamente un deuterone. Per ottenere il deuterone, uno dei due neutroni deve quindi trasformarsi in un protone. Il passaggio da \( I_3 = -\tfrac12 \) a \( I_3 = +\tfrac12 \) avviene tramite l’emissione di un pione negativo \( \pi^{-} \):
\[ n + n \rightarrow n + p + \pi^{-} \]
A questo punto la coppia \( p + n \) può legarsi formando il deuterone \( d \), che ha isospin \( I = 0 \) e proiezione \( I_3 = 0 \). Il pione \( \pi^{-} \) ha isospin \( I = 1 \) e proiezione \( I_3 = -1 \). Il prodotto finale è quindi:
\[ n + n \rightarrow d + \pi^{-} \]
La conservazione della proiezione di isospin risulta evidente:
\[ \underbrace{n + n}_{I_3 = -\tfrac12 - \tfrac12 = -1} \longrightarrow \underbrace{d + \pi^{-}}_{0 + (-1) = -1} \]
Anche in questo caso, come nell’esempio \( p + p \), la formazione del deuterone richiede la trasformazione di uno dei due nucleoni, in modo tale da ottenere la coppia \( p + n \) che può formare uno stato legato.
Nella notazione a ket di Dirac, sapendo che ogni neutrone è $ n = | \frac12 \ - \frac12 \rangle $, si scrive
\[ nn = |1 \ -1\rangle \longrightarrow |0\ 0\rangle \otimes |1\ -1\rangle = |1\ -1\rangle \]
A sinistra c’è \( nn = |1\ -1\rangle \), a destra c’è ancora \( |1\ -1\rangle \), quindi la simmetria di isospin è rispettata.
Dall’isospin a SU(3): la Via degli Otto
L’isospin descrive una simmetria interna che mette in relazione protone e neutrone come due stati di uno stesso sistema.
Tuttavia, l’aumento del numero di particelle scoperte negli anni Cinquanta mostrò che questa simmetria non era sufficiente a organizzare l’intero panorama degli adroni.
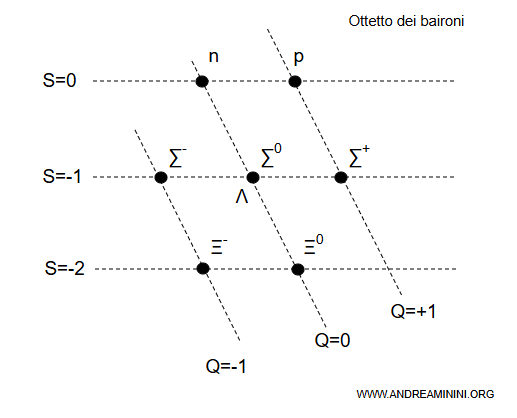
Accanto ai nucleoni comparvero infatti altri barioni, come \( \Lambda \), \( \Sigma \) e \( \Xi \), con proprietà molto simili ma differenti valori di carica e stranezza.
Questo suggerì l’esistenza di una simmetria più ampia, capace di includere l’isospin come sottostruttura.
La Via degli Otto (Eightfold Way) rappresenta questa estensione concettuale.
Introduce una simmetria di sapore descritta dal gruppo SU(3), che permette di classificare gli adroni in multiplette regolari e trova il suo fondamento microscopico nel modello a quark.
Note
Alcune note utili sulla simmetria e l'isospin
- Relazione tra carica elettrica e isospin
La carica \( Q \) di una particella dipende dalla componente di isospin \( I_3 \) secondo la formula di Gell-Mann - Nishijima: $$ Q = I_3 + \frac{1}{2}(A + S) $$ Dove \( A \) è il numero barionico e \( S \) è la stranezza (strangeness). Questa formula vale per gli adroni scoperti prima del 1974, cioè quelli costruiti solo da quark ( u, d, s ). Allo stato della particella con la carica elettrica più alta si assegna il massimo valore di isospin $ I_3 = I $ e poi si scende via via gli altri membri del multipletto riducendo \( Q \). - Il limite della simmetria tra protone e neutrone
Le forze forti non risultano identiche per un protone e un neutrone considerati singolarmente, ma solo in uno scambio simultaneo di tutti i protoni con tutti i neutroni del sistema. Sostituire un singolo protone con un neutrone non riproduce lo stesso stato quantico, perché ciò violerebbe il principio di esclusione di Pauli.
E così via.
