Pseudovettore

Gli pseudovettori, detti anche vettori assiali, sono vettori che non cambiano il segno dopo una riflessione spaziale, cioè una simmetria centrale.

Gli pseudovettori sono grandezze fisiche che si comportano come vettori nelle rotazioni, ma non si trasformano come i vettori ordinari dopo un'inversione delle coordinate dello spazio (operazione di parità).

In altre parole, quando effettuo una trasformazione di parità, un vettore ordinario (o polare) cambia verso, mentre uno pseudovettore non cambia segno.

Per capire bene la differenza tra un vettore ordinario e uno pseudovettore è molto utile fare un esempio.

Un  esempio pratico

Esempio di vettore ordinario

Considero un vettore ordinario $ \vec v $

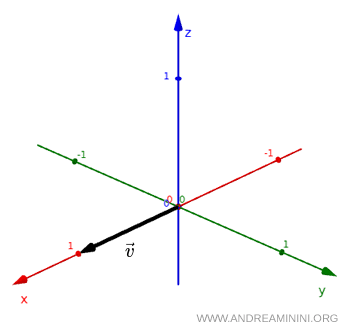
Se effettuo un'inversione spaziale, cioé $ x \to -x $ e $ y \to -y $, il vettore si trasforma nel suo vettore opposto $ - \vec v $.

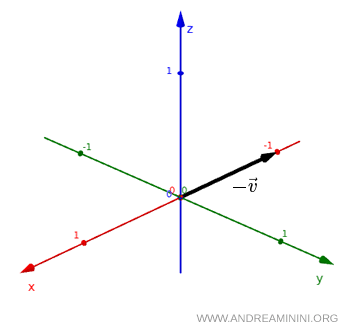
Il nuovo vettore $ - \vec v $ ha la stessa direzione e la stessa intensità, ma verso opposto rispetto a quello iniziale ( $ \vec v $ ).

In altre parole, il vettore ha cambiato segno dopo l'inversione spaziale.

Questo significa che, osservando un vettore ordinario nello spazio riflesso, la sua lunghezza resta invariata, mentre il verso si inverte.

Nota. Alcuni esempi di vettori ordinari in fisica sono il vettore spostamento, la velocità, la forza, ecc.

Viceversa, uno pseudovettore resta invariato dopo una riflessione spaziale.

Esempio di pseudovettore

Un esempio classico di pseudovettore è il momento angolare.

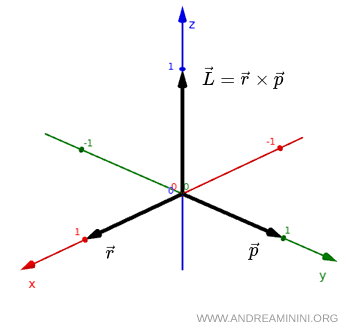
Se prendo un vettore posizione $ \vec r $ e un vettore quantità di moto $ \vec p $, il momento angolare è definito come il prodotto vettoriale dei due vettori:

$$ \vec L = \vec r \times \vec p $$

In generale, il prodotto vettoriale di due vettori genera sempre uno pseudovettore.

Se osservo il sistema allo specchio, i vettori $ \vec r $ e $ \vec p $ si trasformano rispettivamente in $ - \vec r $ e $ - \vec p $. Tuttavia, il loro prodotto vettoriale mantiene lo stesso verso.

$$ \vec L = \vec r \times \vec p = ( - \vec r ) \times ( - \vec p ) $$

In entrambi i casi, il prodotto vettoriale $ \vec L $ è lo stesso vettore perpendicolare al piano individuato da $ \vec r $ e $ \vec p $ orientato lungo l'asse $ z $ nello stesso verso.

 

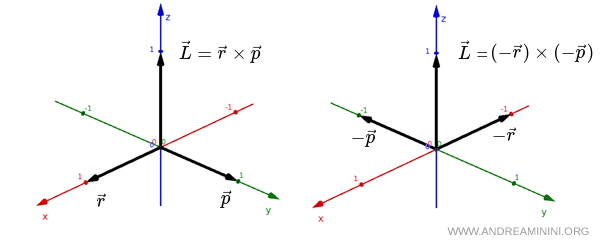
Quindi, lo pseudovettore $ \vec L $ non ha cambiato segno dopo l'inversione spaziale.

Nota. Altri esempi di pseudovettori in fisica sono la velocità angolare, il momento torcente e il campo magnetico.Tutti questi derivano da un prodotto vettoriale.

Qual è il significato fisico degli pseudovettori?

Gli pseudovettori rivelano una proprietà profonda dello spazio: alcune grandezze non dipendono solo dalla direzione, ma anche dall’orientazione dello spazio stesso.

Questo è il motivo per cui entrano in gioco quando si studiano fenomeni legati alla parità, come nella fisica delle interazioni fondamentali.

In particolar modo, in fisica sono molto utili per capire la violazione della parità nella interazione debole.

E così via.