La simmetria centrale

La simmetria centrale è una trasformazione geometrica che mappa ogni punto A della figura su un punto A' rispetto a un punto fisso P scelto come centro di simmetria, in modo che P diventi il punto medio del segmento che congiunge A e A'

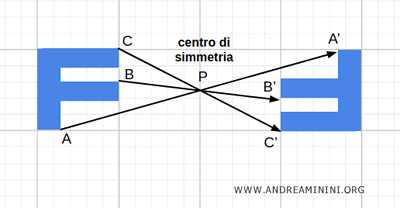
La simmetria centrale è una isometria perché mantiene costanti le distanze relative tra i punti di una figura.

Il centro di simmetria P è il punto unito della trasformazione.

Può essere ottenuta sia sul piano che nello spazio euclideo a tre dimensioni.

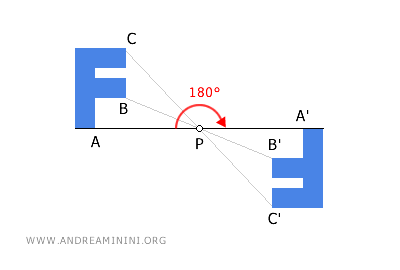
Sul piano la simmetria centrale può essere considerata come una rotazione di 180° intorno a un a centro di simmetria. Nello spazio tridimensionale, invece, è una isometria invertente.

Un esempio pratico

La simmetria centrale è una trasformazione geometrica che opera in relazione a un punto fisso, noto come centro di simmetria.

Questo punto, indicato con la lettera P, funge da "ancora" per la trasformazione.

Ad esempio, disegno una figura sul piano e scelgo un punto fisso P come centro di simmetria.

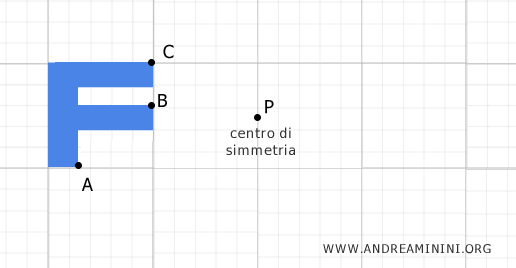
Considero i punti A, B, C della figura.

Poi traccio delle semirette che partono da ciascuno di questi punti (A,B,C) e attraversano il centro di simmetria P.

 

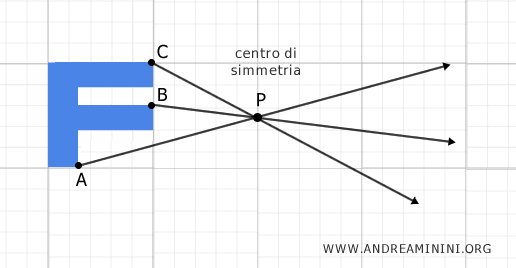
A questo punto, ogni punto della figura deve essere mappato su un altro punto, in modo tale che P diventi il punto medio del segmento.

Ad esempio, nel caso del punto A, individuo il punto corrispondente A' che si trova sulla stessa retta, alla stessa distanza da P come A, ma nella direzione opposta.

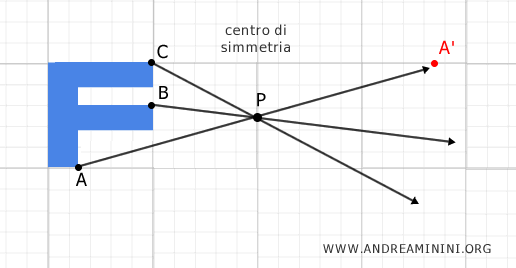
Questi due punti, A e A', sono detti punti simmetrici rispetto al punto P.

Il centro di simmetria P si trova esattamente nel punto medio del segmento AA'. In altre parole, il segmento AA' è diviso a metà dal punto P.

$$ \overline{AP} \cong \overline {A'P} $$

Ripeto lo stesso procedimento per tutti i punti della figura e ottengo la figura ruotata di 180°.

 

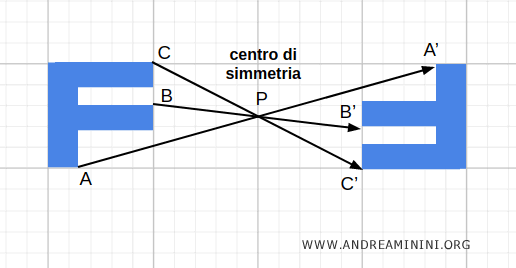
Nota. Un altro modo per immaginare la simmetria centrale sul piano è pensare di ruotare una figura di 180° attorno al suo centro di simmetria P. Questa trasformazione genera una figura che è l'immagine speculare dell'originale ma è sempre congruente ad essa, perché le distanze tra i punti sono sempre le stesse.

Le figure ottenute attraverso la simmetria centrale sono sempre congruenti tra loro, perché hanno la stessa forma e dimensione, anche se possono avere orientamenti diversi nello spazio.

Poiché preserva le distanze tra i punti, la simmetria centrale è considerata una isometria.

Le equazioni

Nel piano la simmetria centrale di qualsiasi punto P(x;y) rispetto a un altro punto C(x₀;y₀) preso come centro di simmetria, può essere ottenuta applicando queste equazioni

$$ \begin{cases} x' = 2x_0 - x \\ \\ y' = 2y_0 - y \end{cases} $$

Nota. Se scelgo il centro degli assi cartesiani O(0;0) come centro di simmetria, la simmetria centrale si ottiene semplicemente usando le coordinate opposte di ogni punto. In questo caso x₀=0 e y₀=0. Quindi, se il centro di simmetria è l'origine, due punti simmetrici rispetto all'origine degli assi cartesiani hanno le rispettive coordinate opposte $$ \begin{cases} x' = - x \\ \\ y' = - y \end{cases} $$

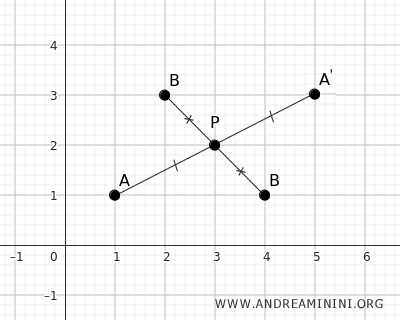
Ad esempio, scelgo il punto P alle coordinate P(x₀;y₀)=(3;2) come centro di simmetria

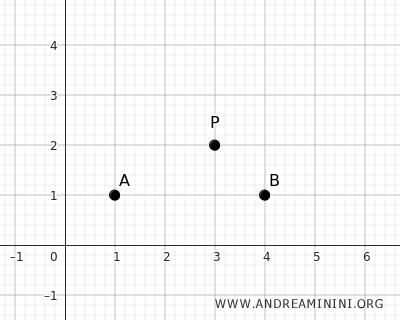
Poi aggiungo due punti A(1;1) e B(4;1) sul piano.

Utilizzo le equazioni per calcolare il punto corrispondente A'

Il punto A si trova alle coordinate x=1 e y=1 mentre il centro di simmetria alle coordinate x₀=3 e y₀=2.

$$ \begin{cases} x' = 2x_0 - x \\ \\ y' = 2y_0 - y \end{cases} $$

$$ \begin{cases} x' = 2 \cdot 3 - 1 \\ \\ y' = 2 \cdot 2 - 1 \end{cases} $$

$$ \begin{cases} x' = 6 - 1 \\ \\ y' = 4 - 1 \end{cases} $$

$$ \begin{cases} x' = 5 \\ \\ y' = 3 \end{cases} $$

Il punto corrispondente A' si trova alle coordinate x'=5 e y'=3.

Il centro di simmetria P è il punto medio del segmento AA'

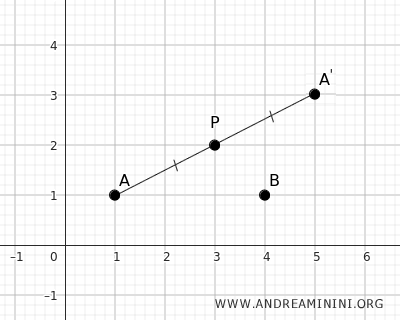
Ora utilizzo le equazioni per calcolare il punto corrispondente B'

Il punto B si trova alle coordinate x=4 e y=1 e il centro di simmetria è sempre alle coordinate x₀=3 e y₀=2.

$$ \begin{cases} x' = 2x_0 - x \\ \\ y' = 2y_0 - y \end{cases} $$

$$ \begin{cases} x' = 2 \cdot 3 - 4 \\ \\ y' = 2 \cdot 2 - 1 \end{cases} $$

$$ \begin{cases} x' = 6 - 4 \\ \\ y' = 4 - 1 \end{cases} $$

$$ \begin{cases} x' = 2 \\ \\ y' = 3 \end{cases} $$

Pertanto, il punto B' si trova alle coordinate x'=2 e y'=3.

Il centro di simmetria P è il punto medio del segmento BB'

Da notare che entrambe le simmetrie centrali possono essere viste come una rotazione di 180° dei punti A e B rispetto al punto P.

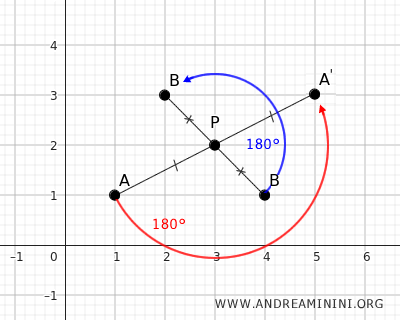
Al termine della trasformazione la distanza tra i due punti A' e B' è la stessa.

La dimostrazione. La simmetria centrale è una trasformazione geometrica che fa corrispondere a ogni punto P(x;y) del piano un altro punto P'(x';y') detto immagine di P rispetto a un punto M(x_M;y_M) scelto come centro di simmetria. Se traccio un segmento tra i due punti PP', il punto M è il punto medio del segmento. Quindi, posso scrivere l'equazione del punto M usando le formule del punto medio di un segmento $$ \begin{cases} x_M = \frac{x+x'}{2} \\ \\ y_M = \frac{y+y'}{2} \end{cases} $$ Da queste ricavo algebricamente le coordinate (x';y') dell'immagine P' di un qualsiasi punto P(x;y) del piano rispetto al centro di simmetria M(x_M;y_M). $$ \begin{cases} x' = 2x_M - x \\ \\ y' = 2y_M-y \end{cases} $$ Nel caso particolare in cui il centro di simmetria corrisponde all'origine degli assi M(x_M;y_M)=(0;0). Sostituisco x_M=0 e y_M=0 nella formula precedente e ottengo le equazioni della simmetria centrale rispetto all'origine del piano. $$ \begin{cases} x' = 2 \cdot 0 - x \\ \\ y' = 2 \cdot 0 -y \end{cases} $$ $$ \begin{cases} x' = - x \\ \\ y' = -y \end{cases} $$

La simmetria centrale nello spazio

La simmetria centrale rispetto a un punto \( O \) nello spazio è una trasformazione geometrica che:

• lascia invariato il punto \( O \)
• associa a ogni punto \( P \), diverso da \( O \), un punto \( P' \) tale che \( O \) sia il punto medio del segmento \( PP' \), ossia \( OP \cong OP' \)

Ecco un esempio pratico:

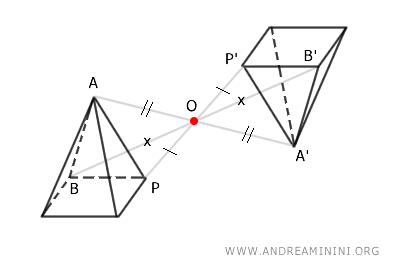
Dove il punto centrale \( O \) è l'unico punto unito (ossia invariato) della trasformazione.

Due solidi che si corrispondono tramite una simmetria centrale nello spazio rispetto a \( O \) sono, in generale, inversamente congruenti.

Nota. Due solidi sono inversamente congruenti se hanno la stessa forma e dimensione, ma una disposizione speculare, ossia non possono essere sovrapposti con un movimento rigido nello spazio senza ribaltamento.

Le funzioni simmetriche rispetto all'origine

Una funzione $f(x)$ è simmetrica rispetto all’origine se e solo se è una funzione dispari, cioè se vale $f(-x) = -f(x)$.

Non tutte le funzioni sono simmetriche rispetto all’origine. Anzi, è una proprietà speciale che riguarda solo alcune funzioni.

La maggior parte delle funzioni reali che incontriamo non è simmetrica né rispetto all’asse y (funzioni pari), né rispetto all’origine (funzioni dispari).

Nota. Una funzione è dispari se soddisfa la relazione $ f(-x)=-f(x) $, è pari se soddisfa la relazione $ f(-x) = f(x) $

Esempio

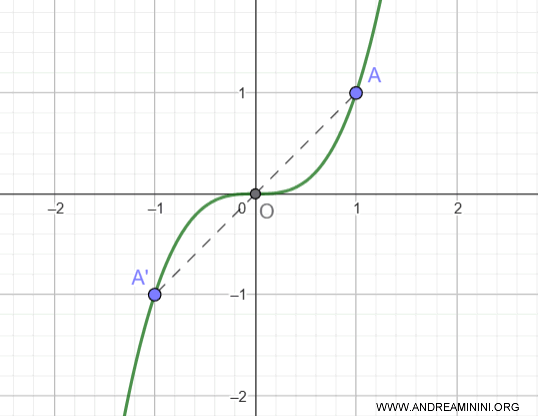
La funzione $f(x) = x^3$ è dispari, perché:

$$ f(-x) = (-x)^3 = -x^3 = -f(x) $$

Il suo grafico è simmetrico rispetto all’origine.

Esempio 2

La funzione $f(x) = x^2$ non è dispari. 

$$ f(-x) = (-x)^2 = x^2 \ne -f(x) = - x^2 $$

E' una funzione pari perché ha simmetria rispetto all’asse y. 

$$ f(-x) = (-x)^2 = x^2 = f(x) $$

Quindi, non è simmetrica rispetto all'origine.

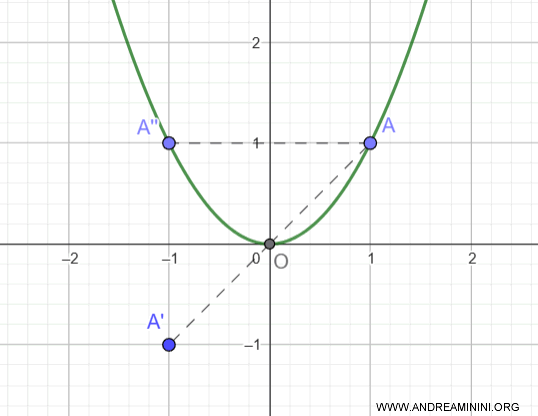
Esempio 3

La funzione $ f(x)=x+1 $ non è dispari, né dispari

$$ f(-x) = ( -x+1) = -x+1 $$

Poiché $f(-x) $ è diverso sia da $f(x) =  x + 1 $ che da $-f(x) = -(x + 1) = -x - 1 $, la funzione non presenta alcuna simmetria, né rispetto all’asse $y$, né rispetto all’origine.

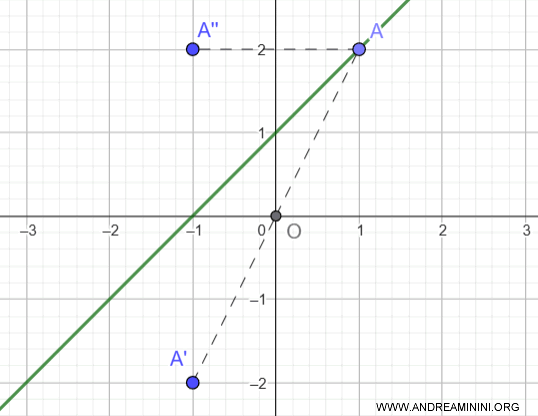
Quindi non è né una funzione pari, né una funzione dispari.

Dimostrazione

Dire che una funzione ha simmetria centrale rispetto all’origine (0, 0) significa che se un punto $(x, y)$ appartiene alla curva, anche il punto opposto $(-x, -y)$ deve appartenere alla curva.

$$ \begin{cases} x' =  - x \\ \\ y' = - y \end{cases} $$

In altre parole, un punto qualsiasi $(x, f(x))$ sulla curva dopo la simmetria centrale diventa $(-x, -f(x))$.

Se applico questa simmetria a una funzione $y = f(x)$ ottengo:

$$ y = -f(-x) $$

Sapendo che $ y = f(x) $

$$ f(x) = -f(-x) $$

Quindi, perché la funzione originale sia uguale alla sua versione riflessa, dev’essere soddisfatta la relazione $ f(x) = -f(-x) $

Moltiplico entrambi i lati dell'equazione per -1 

$$ f(x) \cdot (-1) = -f(-x) \cdot (-1) $$ 

$$ - f(x) = f(-x) $$

O, equivalentemente:

$$ f(-x) = -f(x) $$

Questa è la definizione di funzione dispari.

Osservazioni

Alcune osservazioni sulla simmetria centrale

• La figura ottenuta con la simmetria centrale è congruente alla figura originale
  La simmetria centrale è un'isometria e, pertanto, preserva le distanze tra i punti di una figura. Questo significa che le figure risultanti hanno lati e angoli congruenti e sono, di conseguenza, congruenti tra loro. Pertanto, la distanza relativa tra i punti è un invariante della simmetria centrale.
  
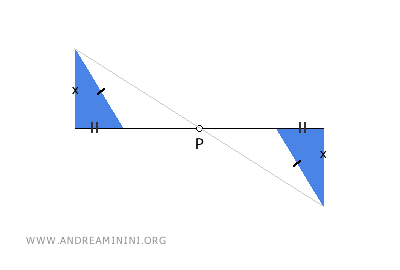
• Gli invarianti della simmetria centrale
  La posizione del centro di simmetria P sul piano è un invariante della simmetria centrale. Un altro invariante è la direzione delle rette. Sono invarianti anche le distanze relative tra i punti della figura.
• La composizione di due simmetrie centrali nello stesso centro genera l'identità
  Se considero una figura e applico una sequenza di due trasformazioni isometriche centrali nello stesso centro P, una dopo l'altra, ciò che ottengo è la stessa figura iniziale. In altre parole, la figura ritorna alla sua posizione e forma originale, come se non fosse stata sottoposta a nessuna trasformazione. Pertanto, la composizione è una trasformazione involutoria.
  
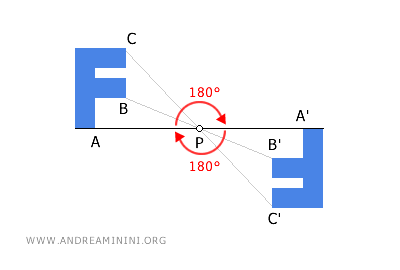
  In generale, la composizione di un numero pari di simmetrie centrali nello stesso centro di simmetria genera sempre una identità.
• La simmetria centrale non è un'operazione interna
  In generale, la composizione di due o più simmetrie centrali non è detto che generi una simmetria centrale. Quindi, la simmetria centrale non è un'operazione interna alla simmetria centrale. Ad esempio, questa composizione di simmetrie centrali nei centri P e P' produce come risultato finale una traslazione verso il basso della figura iniziale. Quindi, il risultato finale non è una simmetria centrale.
  
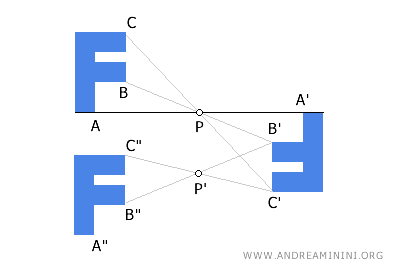
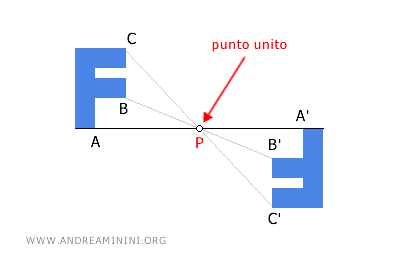
• Il centro di simmetria è un punto unito ed è l'unico
  Nella simmetria centrale il centro di simmetria è un punto che non modifica la sua posizione sul piano dopo la trasformazione geometrica. Ha se stesso come immagine. Pertanto, è un "punto unito". Questo dimostra che la posizione del centro è un invariante della simmetria centrale. Inoltre, va sottolineato che è anche l'unico punto unito possibile nella simmetria centrale.
  
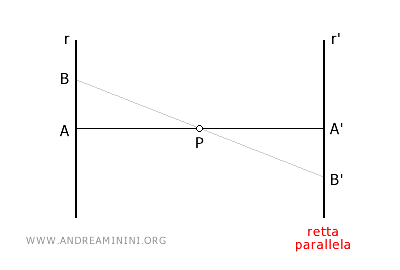
• Nella simmetria centrale le rette sono parallele
  Qualsiasi retta riflessa rispetto a un centro di simmetria ha come trasformata una retta parallela. Quindi, il parallelismo delle rette è un invariante della simmetria centrale.
  
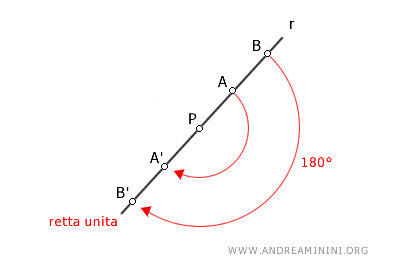
• Ogni retta che passa per l'origine è una retta unita
  Nella simmetria centrale qualsiasi retta passante per l'origine ha come trasformata una retta coincidente. Pertanto, è una "retta unita" perché occupa gli stessi punti del piano.
  
• Il centro di simmetria di una figura
  Un punto del piano è detto centro di simmetria di una figura se, scelto come centro della simmetria centrale, genera come trasformata una figura che occupa gli stessi punti del piano. In altre parole, è un punto centrale (se esiste) che rende la figura "unita" rispetto alla simmetria centrale. Ad esempio, il centro di un rettangolo, di un quadrato, di un rombo, di un cerchio, ecc.
  
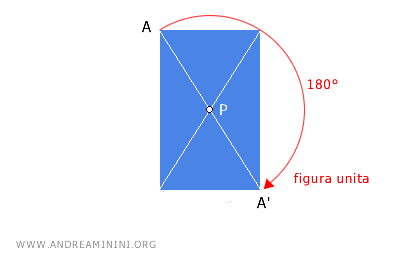
• La simmetria centrale è una trasformazione involutoria
  La simmetria centrale $ T $ è una trasformazione involutoria, perché la sua inversa $ T^{-1} $ coincide con sé stessa: $$ T^{-1}  = T $$ Di conseguenza: $$ T^{-1} \circ T = T \circ T^{-1} =  \text{id} $$ Applicarla due volte equivale a eseguire la trasformazione identica, cioè ogni punto torna nella posizione iniziale. $$ T \circ T = \text{id} $$
• La composizione di due simmetrie centrali equivale con centri distinti a una traslazione
  La composizione di due simmetrie centrali $S_{M_1}$ e $S_{M_2}$, aventi rispettivamente centro in $M_1$ e $M_2$, è equivalente a una traslazione di vettore di modulo pari al doppio della lunghezza del segmento $ \overline{M_1M_2} $ $$ S_{M_1} \circ S_{M_2} \leftrightarrow \vec{v} = 2\,\overrightarrow{M_1 M_2} $$ 

  Esempio. Prendo un punto $A$, faccio la sua simmetria centrale rispetto a $M_1$ e ottengo il punto $B$. Poi prendo $B$, faccio la simmetria centrale rispetto a $M_2$ e  ottengo il punto $C$.
  
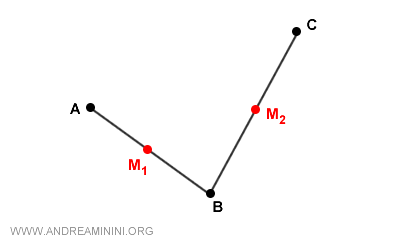
  In pratica, passando da $A$ a $B$ e poi da $B$ a $C$, il risultato finale è lo stesso che se avessi spostato $A$ direttamente in $C$ con una traslazione. Questa traslazione ha come vettore $  \vec{v} = 2\,\overrightarrow{M_1 M_2} $ cioè è lunga il doppio del segmento che congiunge i punti medi $M_1M_2$ e punta nella stessa direzione.
  
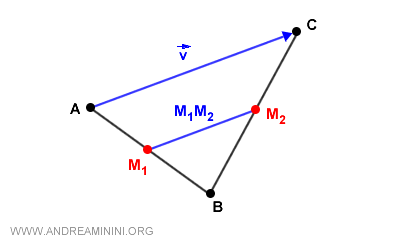
  Dimostrazione Il vettore $ \vec{v} = 2\,\overrightarrow{M_1 M_2} $ ha modulo (cioè lunghezza) pari al doppio del segmento che unisce i centri $\overline{M_1 M_2}$ perché i punti $A$, $B$ e $C$ formano un triangolo $ ABC $ in cui $M_1$ e $M_2$ sono, rispettivamente, i punti medi dei lati $AB$ e $BC$. Per il teorema dei punti medi di un triangolo, il segmento  $\overline{M_1 M_2}$ che congiunge i punti medi di due lati ( $ AB $ e $ BC $ ) è parallelo e lungo la metà del lato rimanente ( $AC$ ) del triangolo. Questo dimostra che il vettore di traslazione $\vec{v}$ ha sempre una lunghezza doppia rispetto al segmento $\overline{M_1 M_2}$ e la stessa direzione.

E così via