Antiparticelle
Ogni particella elementare ha in generale una antiparticella corrispondente con la stessa massa, lo stesso spin ma con cariche additive opposte (elettrica, barionica, leptonica, ecc.)
L’antiparticella è un'entità distinta con un ruolo fisico preciso nelle interazioni.
Ecco alcuni esempi
| Particella | Antiparticella |
|---|---|
| Elettrone $e^-$ | Positrone $e^+$ |
| Protone $p $ | Antiprotone $\overline{p} $ |
| Neutrone $n $ | Antineutrone $\overline{n} $ |
| Quark $u $ | Antiquark $\overline{u} $ |
Ad esempio, l'antiparticella dell'elettrone (carica elettrica negativa) è il positrone che ha la stessa massa e spin ma con carica positiva.
L'antiparticella del protone (carica elettrica positiva) è l'antiprotone che ha carica elettrica negativa, ecc.
Nota. Generalmente le antiparticelle sono indicate ponendo una barra sopra il simbolo della particella. Ad esempio, il protone $ n $ ha come antiparticella l'anti-protone $ \overline{p} $. Tuttavia, ci sono alcune eccezioni. Per indicare il positrone (anti-elettrone) spesso si usa il simbolo $ e^+ $ anziché $ \overline{e} $, per indicare l'antimuone si usa $ \mu^+ $ anziché $ \overline{ \mu } $.
Va detto che non necessariamente la carica elettrica deve essere opposta, un'antiparticella potrebbe anche avere un'altra carica additiva opposta, come la carica barionica o la carica leptonica, o altri numeri quantici.
Ad esempio, il neutrone ha carica elettrica nulla. Quindi, l'antineutrone non può avere una carica elettrica opposta. A distinguere l'antineutrone dal neutrone sono altri numeri quantici.
Esistono anche particelle che hanno le antiparticelle identiche, queste sono dette particelle autoconiugate.
Una particella autoconiugata è identica alla propria antiparticella quando la carica elettrica è nulla e tutte le altre cariche additive sono nulle.
Ecco alcuni esempi di particelle autoconiugate:
| Particella | Autoconiugata? | Note |
|---|---|---|
| Fotone $ \gamma $ | si | Nessuna carica |
| Bosone $Z^0 $ | si | Neutro |
| Mesone $\pi^0 $ | si | Pione neutro |
| Gluoni | si / no | Dipende dalla combinazione |
Nel caso dei neutrini, non è ancora certo se siano neutrini di Dirac (con antiparticella distinta) o neutrini di Majorana (autoconiugati). Questo è un tema aperto nella fisica delle particelle.
La differenza tra antiparticelle e antimateria
La materia composta interamente da antiparticelle è detta antimateria.
L'antimateria ha una caratteristica particolare, quando materia e antimateria si incontrano, si annichilano, liberando energia sotto forma di fotoni γ.
$$ e^- + e^+ \rightarrow \gamma + \gamma $$
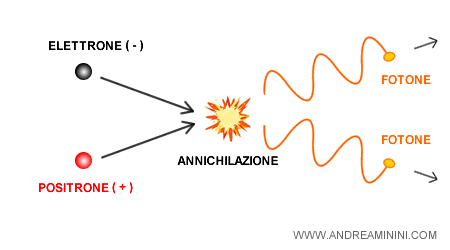
Va detto che per parlare di antimateria non è sufficiente l’esistenza di un singolo positrone: serve un sistema strutturato come un anti-atomo o una molecola stabile di antimateria.

In altre parole, l’antimateria è composta da antiparticelle ma non tutte le antiparticelle formano antimateria.
Esempio. Un atomo di anti-idrogeno è formato da un antiprotone \$\overline{p}\$ nel nucleo e da un positrone \$e^+\$ (elettrone di antimateria) che vi orbita intorno. Rispetto all'atomo di idrogeno, le cariche elettriche del protone e dell'elettrone sono invertite. Poiché queste antiparticelle formano una struttura stabile e neutra, l’atomo di anti-idrogeno è un esempio di antimateria. Viceversa, un positrone isolato, o un antineutrino che viaggia nello spazio, non sono antimateria: sono singole antiparticelle.
Quindi, l'antimateria e le antiparticelle non sono la stessa cosa, anche se sono strettamente collegate.
L'antimateria è una forma strutturata di materia composta da antiparticelle legate insieme in modo stabile, mentre le antiparticelle possono anche esistere isolate, senza formare antimateria.
La scoperta delle antiparticelle
Nel 1927, il fisico Paul Dirac cercava un’equazione che descrivesse il comportamento degli elettroni liberi in modo coerente sia con la meccanica quantistica che con la relatività.
Ci riuscì: l'equazione:
$$ E^2−p^2c^2=m^2c^4 $$
Ma c’era un problema, l’equazione dava due tipi di soluzioni per l’energia:
$$ E = \pm \sqrt{p^2 c^2 + m^2 c^4} $$
La soluzione positiva $ E = + \sqrt{p^2 c^2 + m^2 c^4} $ è quella che ci si aspetta, l’elettrone ha energia maggiore di zero come ogni particella normale.
La soluzione negativa $ E = - \sqrt{p^2 c^2 + m^2 c^4} $ ammette, invece, che l'elettrone potrebbe esistere anche in uno stato con energia negativa.
Ma cosa succede se un elettrone può accedere a questi stati negativi?
Secondo la meccanica quantistica, ogni sistema tende spontaneamente ad abbassare la propria energia.
Un elettrone che si trova in uno stato a energia positiva, dunque, cercherebbe di passare a stati con energia più bassa.
Ma l’equazione di Dirac ammette anche infiniti stati a energia negativa: se questi fossero accessibili, l’elettrone potrebbe precipitare all’infinito verso energie sempre più negative, emettendo un fotone a ogni transizione.
Il risultato sarebbe un collasso catastrofico: la materia perderebbe continuamente energia, fino a svuotarsi completamente.
Per evitare questo paradosso, Dirac avanzò un’ipotesi audace: tutti gli stati a energia negativa sono già occupati da elettroni invisibili, formando quello che chiamò il "mare di Dirac".
Questo mare di elettroni sarebbe ovunque, ma del tutto invisibile perché perfettamente uniforme e inerte: non esercita forze e non interagisce con la materia ordinaria.
Se per qualche ragione uno di questi stati si liberasse, cioè si creasse un “buco” nel mare, allora questo buco si comporterebbe come una particella con carica positiva, energia positiva e la stessa massa dell’elettrone.
Questa particella è ciò che oggi chiamiamo positrone: l’antiparticella dell’elettrone.
Nota. Inizialmente Dirac pensò che questi "buchi" fossero dei protoni. Tuttavia, scartò questa idea perché il protone ha una massa migliaia di volte più grande di un elettrone.
Nel 1932 il primo positrone fu osservato sperimentalmente da Carl Anderson e questa scoperta sembrò dare ragione a Dirac.
L'idea del "mare di elettroni" di Dirac venne però abbandonata negli anni '40, quando Stueckelberg e Feynman considerarono i positroni come vere antiparticelle a energia positiva.
Da allora i positroni sono considerati particelle reali, non “buchi” in un mare immaginario.
Successivamente si diffuse l'idea che ogni particella avesse un'antiparticella con la stessa massa ma carica elettrica opposta.
Negli anni '50 gli esperimenti di Berkeley Bevatron portarono alla scoperta dell'antiprotone e dell'antineutrone.
La simmetria di crossing
La simmetria di crossing consente di ottenere nuovi processi teoricamente equivalenti a uno noto, semplicemente scambiando una particella con la sua antiparticella e spostandola dall’altro lato dell’equazione di reazione.
È una simmetria teorica fondamentale nella fisica delle particelle:
Esempio
La diffusione Compton e l’annichilazione elettrone-positrone sono due processi fisici collegati da questa simmetria.
La diffusione Compton è un processo fisico reale e ben osservato in laboratorio:
$$\gamma + e^- \rightarrow \gamma + e^-$$
Un fotone (γ) colpisce un elettrone libero, si disperde (cambia direzione e lunghezza d'onda), e l’elettrone viene deviato.
È un classico esempio di scattering (diffusione): particella + particella → particella + particella.
Secondo la simmetria di crossing, se un certo processo è possibile, allora sono ammessi (almeno a livello teorico) anche altri processi equivalenti ottenuti spostando le particelle da un lato all’altro dell’equazione e sostituendole con le antiparticelle.
Riprendo il processo di diffusione Compton:
$$ \gamma + e^- \rightarrow \gamma + e^- $$
Applicando la simmetria di crossing, posso trasformare questo processo in un altro teoricamente equivalente.
Sposto il fotone iniziale al secondo membro, trasformandolo nella sua antiparticella che è... un altro fotone perché il fotone è autoconiugato:
$$ e^- \rightarrow \gamma + \gamma + e^- $$
Poi sposto l’elettrone finale $ e^- $ al primo membro, trasformandolo nella sua antiparticella: il positrone $ e^+ $.
$$ e^- + e^+ \rightarrow \gamma + \gamma $$
In questo modo ho ottenuto l’annichilazione elettrone-positrone, un altro processo reale e osservato sperimentalmente.
In altre parole, la simmetria di Compton mi dice che, matematicamente, questi due processi sono manifestazioni diverse dello stesso fenomeno quantistico sottostante.
Questo riflette una profonda unità della fisica: processi apparentemente diversi sono descritti dalle stesse leggi fondamentali.
Attenzione. Anche se i due processi sono matematicamente simmetrci, non sono uguali fisicamente. La diffusione Compton $\gamma + e^- \rightarrow \gamma + e^-$ e l'annichilazione $e^- + e^+ \rightarrow \gamma + \gamma$ sono processi molto diversi. La diffusione di Compton si verifica in un gas o metallo irradiato da fotoni. L'annichilazione si verifica se elettroni e positroni si incontrano e annichiliscono. Quindi, la simmetria riguarda la struttura teorica, non le condizioni pratiche.
E così via.
