La simmetria SU(3) e la Eightfold Way dei barioni

Poiché molti barioni hanno proprietà simili, devono appartenere a una simmetria più ampia dell’isospin. Questa simmetria è SU(3), dove otto barioni con spin \( \tfrac12 \) formano un ottetto. Questo schema di classificazione è detto Eightfold Way (Via degli Otto).

Si parla di simmetria perché le leggi della forza forte rimangono invariate quando si scambiano tra loro certi barioni che hanno proprietà simili.

In altre parole, l’interazione forte non distingue tra questi barioni, che possono essere trasformati l’uno nell’altro senza modificare la fisica del sistema.

Questa invarianza è descritta matematicamente dal gruppo SU(3), che organizza gli otto barioni di spin \( \tfrac12 \) in un’unica struttura, detta "Eightfold Way".

Nota. La Eightfold Way venne introdotta dal fisico teorico statunitense Murray Gell-Mann nel 1961 attraverso la classificazione degli adroni in multiplette organizzate secondo la simmetria SU(3). In questa fase si trattava di uno schema puramente fenomenologico, fondato su regolarità sperimentali e privo di una spiegazione microscopica. Solo in seguito, con l’introduzione del modello a quark nel 1964, proposta dallo stesso Gell-Mann, tale classificazione trovò un fondamento fisico nella composizione interna degli adroni.

Origine della simmetria

Negli anni Cinquanta i fisici scoprirono l’esistenza di numerosi barioni diversi.

In particolare, emerse che otto barioni presentavano proprietà molto simili:

• protone \( p \)
• neutrone \( n \)
• \( \Lambda \)
• \( \Sigma^+ , \Sigma^0 , \Sigma^- \)
• \( \Xi^0 , \Xi^- \)

Queste otto particelle hanno tutte lo spin \( \tfrac12 \), interagiscono tramite la forza forte e le loro masse sono della stessa scala (da circa 940 a 1320 MeV/(c²))

Questo suggerisce che non siano entità indipendenti, ma membri di una stessa famiglia di particelle.

Prima di questi sviluppi, negli anni '30, era già emersa una situazione analoga nel caso del protone e del neutrone, messi in relazione dalla simmetria SU(2). La nuova situazione risultava simile, ma su una scala più ampia.

Nota. Il protone e il neutrone hanno masse quasi uguali e differiscono essenzialmente solo per la carica elettrica. Werner Heisenberg propose che protone e neutrone fossero due stati della stessa particella: il nucleone. Per descrivere questa relazione si introdusse il concetto di isospin, associato al gruppo di simmetria SU(2).

Con la scoperta di nuovi barioni, i fisici si chiesero allora se esistesse un gruppo di simmetria più grande di SU(2), capace di includere tutti e otto questi barioni. Questo interrogativo divenne noto come il problema degli otto barioni.

Per rispondere a questa domanda, Gell-Mann propose che l’isospin SU(2) non fosse la simmetria fondamentale, ma rappresentasse solo una parte di una simmetria più ampia.

Questa simmetria più grande è il gruppo SU(3), all’interno del quale i barioni non risultano raggruppati in modo arbitrario, ma organizzati secondo una struttura di simmetria ben definita.

Nota. Il gruppo SU(3) è un gruppo di simmetria astratto, analogo a SU(2), ma dotato di otto generatori invece di tre. Tra le sue rappresentazioni compare una rappresentazione a otto dimensioni, detta ottetto.

Gli otto barioni $ p, n, \Lambda, \Sigma^+, \Sigma^0, \Sigma^-, \Xi^0, \Xi^- $ formano esattamente un ottetto di SU(3).

Questo schema di classificazione è chiamato Eightfold Way (Via degli Otto).

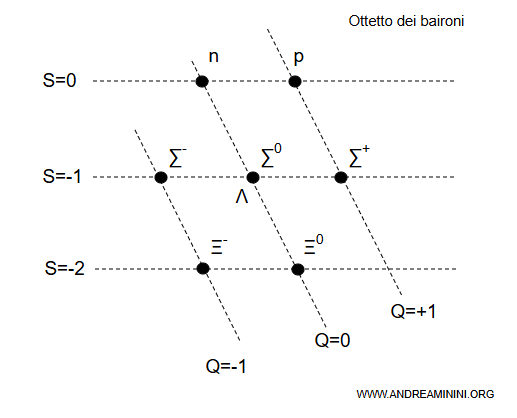
Secondo questa classificazione le otto particelle sono stati diversi di una stessa struttura di simmetria che spiega le relazioni tra quei barioni e permette di prevedere particelle mancanti.

Ad esempio, dallo schema SU(3) venne ipotizzata l’esistenza della particella Ω⁻, scoperta poi sperimentalmente anni dopo.

In altre parole, così come \( p \) e \( n \) sono due stati di un doppietto SU(2), gli otto barioni sono stati di una rappresentazione SU(3).

La Eightfold Way e il modello a quark

La Eightfold Way è uno schema di classificazione, non un modello microscopico della materia.

Negli anni Cinquanta si osservò infatti che molti adroni presentavano proprietà simili e potevano essere organizzati in multiplette che obbedivano a simmetrie come SU(2) (isospin) e SU(3).

Tuttavia, questa regolarità aveva un carattere puramente empirico: non se ne conosceva ancora l’origine fisica, né la struttura interna delle particelle coinvolte.

Con l’introduzione del modello a quark di Murray Gell-Mann e, indipendentemente, di George Zweig, si comprese che gli adroni non sono particelle elementari, ma sistemi composti da costituenti più fondamentali, detti quark.

Nel modello originale compaiono tre quark leggeri: up (u), down (d), strange (s).

quark	carica	isospin	stranezza
u	\( +\tfrac23 \)	\( +\tfrac12 \)	0
d	\( -\tfrac13 \)	\( -\tfrac12 \)	0
s	\( -\tfrac13 \)	0	-1

Questi tre quark \( (u,d,s) \) formano il tripletto fondamentale della simmetria SU(3). Questo è il punto chiave del modello.

La simmetria SU(3) di sapore è infatti la simmetria che mette in relazione i quark \( u \) (up), \( d \) (down) e \( s \) (strange), trattandoli come equivalenti dal punto di vista dell’interazione forte, a meno delle differenze di massa. A partire da questi costituenti fondamentali è possibile comprendere la struttura degli adroni osservati.

In particolare, i barioni risultano essere composti da tre quark.

$$ qqq $$

Combinando tre triplette di SU(3) si ottiene:

$$ 3 \otimes 3 \otimes 3 = 10 \oplus 8 \oplus 8 \oplus 1 $$

Questa scomposizione spiega lo spettro dei barioni:

• 10 è il decupletto barionico con spin \( \tfrac32 \)
• 8 è l'ottetto barionico con spin \( \tfrac12 \)
• 1 è il singoletto (stato isolato)

Quindi, l'esistenza del decupletto e dell'ottetto non è un’ipotesi fisica arbitraria, ma una conseguenza matematica della simmetria SU(3).

Ad esempio, l’ottetto barionico in termini di quark è composto da otto barioni formati dai quark \( (u,d,s) \)

Barione	composizione
p	uud
n	udd
\( \Lambda \)	uds
\( \Sigma^+ \)	uus
\( \Sigma^0 \)	uds
\( \Sigma^- \)	dds
\( \Xi^0 \)	uss
\( \Xi^- \)	dss

Questa composizione non è una coincidenza. La simmetria SU(3) funziona perché gli adroni sono fatti di tre quark (u,d,s).

In pratica, il modello a quark fornisce il fondamento microscopico della Eightfold Way (Via degli Otto) tramite l'introduzione dei quark (u,d,s) che formano il tripletto fondamentale di SU(3).

Dalla combinazione di questi tre quark emergono le multiplette barioniche che erano state osservate dalla Via degli otto.

Nota. La simmetria SU(3) non è una simmetria esatta perché le masse dei quark non sono uguali: $$ m_u \approx m_d \ll m_s $$ Quindi, si tratta di una simmetria approssimata. La stranezza rompe la simmetria ma la struttura resta visibile nei multiplette. In generale, la simmetria SU(2) è molto più accurata

Il decupletto barionico

Dopo aver individuato l’ottetto dei barioni con spin \( \tfrac12 \), alcune osservazioni sperimentali mostravano anche l’esistenza di altri barioni, con proprietà simili ma spin diverso, in particolare con spin \( \tfrac32 \).

Questi stati non potevano essere inseriti nell’ottetto già noto, ma presentavano regolarità troppo evidenti per essere considerate casuali.

Tutto ciò suggeriva che la simmetria SU(3) fosse più ricca di quanto apparisse inizialmente.

Analizzando le configurazioni possibili generate dalla struttura matematica della simmetria SU(3), si scoprì che, oltre all’ottetto (8), erano ammesse anche altre rappresentazioni, tra cui un decupletto (10) e un singoletto (1):

\[ 3 \otimes 3 \otimes 3 = 10 \oplus 8 \oplus 8 \oplus 1 \]

Questa decomposizione non è un’ipotesi fisica, ma una conseguenza rigorosa della teoria delle rappresentazioni.

Nota. In altre parole, se esiste l’ottetto, allora deve esistere anche il decupletto, perché entrambi emergono naturalmente dalla stessa struttura matematica.

Il decupletto barionico corrisponde a configurazioni completamente simmetriche nello spazio dei sapori, e per questo è associato a barioni con spin totale \( \tfrac32 \).

A differenza dell’ottetto, che ha una forma esagonale con un centro, il decupletto ha una struttura a forma di un triangolo equilatero composta da dieci stati distribuiti su quattro livelli.

 

Nota. Lo schema a triangolo non è una semplice rappresentazione grafica, ma riflette una struttura profonda: tutte le particelle del decupletto hanno spin allineato, quindi spin totale \( \tfrac32 \) e la simmetria tra i quark è massima.

Il diagramma è costruito disponendo le particelle in base a due numeri quantici: la stranezza ( $ S $ ) e la carica elettrica ( $ Q $ ).

Procedendo dall’alto verso il basso la stranezza diminuisce e aumenta il numero di quark strange presenti nella particella.

Al vertice superiore del triangolo si trovano quattro particelle $ \Delta $ che non contengono quark strange e sono composti solo da quark up (u) e down (d).

• \( \Delta^{++} = uuu \)
• \( \Delta^+ = uud \)
• \( \Delta^0 = udd \)
• \( \Delta^- = ddd \)

Subito sotto compaiono tre particelle $ \Sigma $ che contengono un quark strange (s) e due quark leggeri up (u) e down (d):

• \( \Sigma^{*+} = uus \)
• \( \Sigma^{*0} = uds \)
• \( \Sigma^{*-} = dds \)

La presenza dello strange rompe leggermente la simmetria e aumenta la massa rispetto alla particella Δ.

Nota. L’asterisco indica che la particella \( \Sigma \) si trova in uno stato con spin \( \tfrac32 \). Si tratta della stessa famiglia di particelle \( \Sigma \) presente nell’ottetto, ma in una configurazione diversa: in questo caso lo spin non è più \( \tfrac12 \), bensì \( \tfrac32 \), perché i tre quark che la compongono hanno gli spin tutti allineati. Ogni quark possiede uno spin intrinseco pari a \( \tfrac12 \), indipendentemente dal fatto che sia up, down o strange. Quando i tre quark hanno gli spin allineati (↑↑↑), il momento angolare totale del sistema assume il valore massimo possibile: \[ \tfrac12 + \tfrac12 + \tfrac12 = \tfrac32 \] Questo corrisponde allo stato di spin del decupletto. Viceversa, quando gli spin non sono tutti allineati (↑↑↓, ↑↓↑, ↓↑↑) il risultato della loro combinazione è uno spin totale pari a: \[ \tfrac12 + \tfrac12 - \tfrac12 = \tfrac12 \] In questo caso si ottiene uno stato con spin \( \tfrac12 \), che appartiene all'ottetto barionico. Di conseguenza, la differenza tra \( \Sigma \) e \( \Sigma^* \) non riguarda la composizione in quark, che rimane la stessa, ma esclusivamente il modo in cui gli spin dei quark si combinano tra loro. Lo stesso ragionamento vale anche per la particella \( \Xi^* \), che rappresenta la versione a spin \( \tfrac32 \) della corrispondente \( \Xi \) dell’ottetto.

Nel livello successivo ci sono altre due particelle $ \Xi $ composte da due quark strange e un quark leggero. La massa aumenta ulteriormente.

• \( \Xi^{*0} = uss \)
• \( \Xi^{*-} = dss \)

Infine, alla base del triangolo si trova un’unica particella $ \Omega^-$ composta esclusivamente da quark strange:

\[ \Omega^- = sss \]

Questa particella rappresenta il punto estremo del decupletto ed è caratterizzata da stranezza -3, carica -1 e spin \( \tfrac32 \).

La previsione della particella \( \Omega^- \)

Il successo più famoso di questa struttura fu proprio la previsione della particella \( \Omega^-  \).

Questa particella occupa il vertice inferiore del decupletto e completa la struttura simmetrica prevista teoricamente, ma al momento della formulazione del modello non era ancora stata osservata.

Quando fu scoperta sperimentalmente nel 1964, confermò in modo spettacolare la validità della simmetria SU(3).

E così via.