Coefficiente beta

In altre parole, il coefficiente beta dice come cambia una forza fondamentale (es. elettromagnetica o forte) quando si esplorano distanze sempre più piccole o energie sempre più alte.

E' un concetto centrale nella teoria quantistica dei campi.

La funzione beta è definita come:

$$ \beta(g) = \mu \frac{d g}{d\mu} $$

Dal punto di vista fisico ha questo significato:

• Se $\beta(g) > 0$ l’interazione aumenta con l’energia (diverge all'ultravioletto).
• Se $\beta(g) < 0$ l’interazione diminuisce con l’energia (libertà asintotica).

Quindi, il coefficiente beta misura come una forza fondamentale cambia con l’energia.

Esempio. Nella QED il coefficiente beta è positivo perché la forza aumenta con l’energia (schermatura). Nella QCD, invece, il coefficiente beta è negativo perché la forza diminuisce con l’energia (anti-schermatura). Questo è alla base di concetti della fisica teorica e della teoria dei campi quantistici come il confinamento, la libertà asintotica e l’evoluzione delle costanti fondamentali della natura.

Esempio

Nella QED (elettrodinamica quantistica) il coefficiente beta è positivo.

$$ \beta(\alpha) > 0 $$

Questo vuol dire che la carica effettiva aumenta con l’energia, creando un fenomeno detto di "schermatura del vuoto".

A breve distanza (alta energia), il fotone "vede" meno polarizzazione, quindi la carica è maggiore.

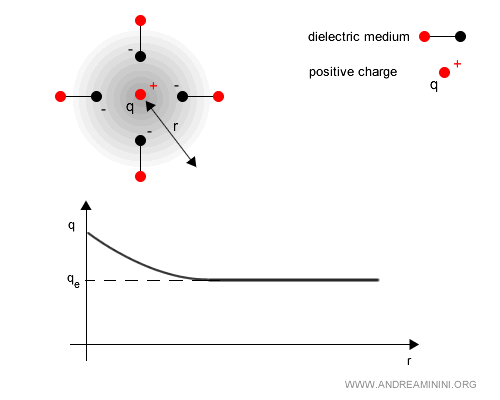
Man mano che ci si allontana la polarizzazione del mezzo dielettrico aumenta e la carica effettiva si riduce.

Esempio. Il vuoto quantistico agisce come un mezzo dielettrico, le fluttuazioni generano coppie virtuali elettrone-positrone che si polarizzano in presenza di una carica $ q $. Se la carica è positiva, le componenti negative delle coppie si avvicinano, quelle positive si allontanano. Questa polarizzazione riduce l’intensità del campo elettrico a grande distanza, facendo apparire la carica effettiva $q_e(r)$ minore della carica reale $q$. In altre parole, la carica reale viene "schermata".

 

Esempio 2

Nella QCD (cromodinamica quantistica) il coefficiente beta è negativo.

$$ \beta(g_s) < 0 $$

Questo significa che la costante di accoppiamento diminuisce con l’energia, creando un fenomeno detto di "anti-schermatura".

Quando i quark sono a distanze molto piccole (alta energia), i quark sembrano quasi liberi (libertà asintotica).

Viceversa, man mano che si allontanano la costante di accoppiamento aumenta e i quark restano confinati dentro l'adrone (es. un protone o un neutrone). Questo fenomeno causa il confinamento dei quark.

La formula del coefficiente beta in QCD

Al primo ordine (1-loop), per la QCD:

$$ \beta(g_s) = - \left( \frac{11}{3} N_c - \frac{2}{3} n_f \right) \frac{g_s^3}{16\pi^2} $$

Dove:

• $N_c = 3$ è il numero di colori
• $n_f$ è il numero di sapori di quark
• $g_s$ è la costante di accoppiamento della forza forte.

Il termine $\frac{11}{3}N_c$ è dovuto ai gluoni virtuali, che contribuiscono a rafforzare l'interazione a grande distanza (anti-schermatura).

Il termine $\frac{2}{3}n_f$ è dovuto alle fluttuazioni dei quark virtuali, che invece tendono a schermare l’interazione, analogamente a ciò che accade in QED.

Finché $n_f < \frac{11}{2}N_c$ il coefficiente $ \beta(g_s) $ resta positivo.

Nota. Poiché i colori sono tre $ N_c = 3 $, questo significa che il coefficiente è positivo $ \beta(g_s) $ se: $$ n_f < \frac{11}{2} \cdot 3 = 16.5 $$ Quindi, tutto dipende dal numero dei sapori $ n_f $. Se il numero di sapori fosse troppo grande, il contributo dei quark prevarrebbe $ \beta > 0 $ e niente libertà asintotica.

Nel caso reale, i sapori sono $ n_f=6 $ quindi $n_f < 16.5$, ossia il coefficiente beta è negativo.

$$ \beta(g_s) < 0 $$

Questo significa che $g_s$ diminuisce con l'aumentare dell’energia.

In altre parole, nella QCD la forza forte si indebolisce a distanze molto piccole.

Questo comportamento dei quark è chiamato libertà asintotica.

Nota. È per questa ragione che, negli urti ad altissima energia come quelli prodotti al CERN, i quark sembrano quasi liberi: l’interazione tra loro si indebolisce via via che li si osserva a distanze più piccole (ovvero a energie più alte).

La formula semplificata

Nella QCD la funzione beta a un-loop può essere espressa così (in unità opportunamente scalate):

$$ \beta(g) \sim -\left(11n - 2f\right) $$

Dove $n = N_c$ (numero dei colori) e $f = n_f$ (numero dei sapori).

In molti testi, per sintesi, si raggruppano i fattori insieme, ottenendo:

$$ \beta \propto -(11n - 2f) = 2f - 11n $$

Quindi una forma comune è:

$$ \beta \sim (2f - 11n) $$

I gluoni danno un contributo a $11N_c$ (anti‑schermatura) mentre i quark (sapori) danno un contributo a $-2n_f$ (schermatura, come in QED).

Nella QCD la funzione diventa beta negativa quando $11n > 2f$, condizione che garantisce la libertà asintotica.

Nota. Questa forma semplificata è utile per studiare schemi generali, specie per variabili $N_c, n_f$ generiche (es., modelli supersimmetrici o ad alte dimensioni) ed evidenziare la concorrenza tra i contributi di gluoni e quark nella funzione beta.

E così via.