Simmetria CP
La simmetria CP è la trasformazione che combina l’inversione spaziale con lo scambio di una particella con la sua antiparticella e lascia invariati, in molti processi, i risultati delle interazioni.
Siamo abituati a pensare che destra e sinistra siano equivalenti, ossia che uno specchio non dovrebbe cambiare le leggi della natura.
Questa è un’aspettativa istintiva... ma non è un fatto fisico, perché in natura a volte la simmetria viene violata.
Ad esempio, la simmetria P (o parità P) viene violata nelle interazioni deboli, dove se guardo un processo non ottengo o stesso processo. Quindi la natura distingue tra destra e sinistra.
La simmetria CP attenua la rottura della simmetria destra - sinistra, pur non essendo una simmetria esatta della natura.
Come funziona?
La simmetria CP è un'azione combinata della parità (P) e della coniugazione di carica (C)
- Guardo un processo allo specchio tramite l'operazione di parità (P)
- Scambio le particelle con le antiparticelle tramite la coniugazione di carica (C)
Se, dopo queste due trasformazioni, il processo risultante coincide con quello iniziale, allora il processo soddisfa la simmetria CP.
In caso contrario, si dice che il processo viola la simmetria CP.
Quindi, la simmetria CP può essere valida anche in situazioni in cui la natura non rispetta la simmetria destra - sinistra.
Nota. Questo non rende il mondo realmente simmetrico, ma mostra che esiste una simmetria più ampia che in molti processi è ancora rispettata. In ogni caso, la fisica non cambia: i fenomeni osservati restano gli stessi.
Un esempio pratico
Verifico la simmetria CP nel decadimento del pione.
\[ \pi^+ \rightarrow \mu^+ + \nu_\mu \]
Per chiarezza, considero separatamente l’effetto della parità P e poi della coniugazione di carica C, pur trattandosi di un’unica trasformazione combinata CP, indipendente dall’ordine con cui le due operazioni vengono applicate.
Nota. Nel decadimento debole il neutrino \( \nu_\mu \) è sempre sinistrorso, l’antineutrino \( \bar\nu_\mu \) è sempre destrorso. Questo è un fatto sperimentale assodato ed è essenziale per comprendere l’esempio.
1] Parità (P)
La parità P inverte lo spazio: \( \vec r \to -\vec r \). Di conseguenza, anche la quantità di moto cambia verso:
$$ \vec p \to -\vec p $$
Lo spin \( \vec s \), invece, non cambia segno perché è un vettore assiale.
Poiché l'elicità dipende dal prodotto scalare \( \vec s \cdot \vec p \), cambia segno sotto l'azione di P:
\[ \vec s \cdot \vec p \to \vec s \cdot (-\vec p)= -(\vec s \cdot \vec p) \]
Pertanto, una particella destrorsa diventa sinistrorsa e viceversa,
Applicando la parità al decadimento del pione, le particelle coinvolte restano le stesse:
\[ P ( \pi^+ ) \rightarrow P ( \mu^+ ) + P ( \nu_\mu ) \]
\[ \pi^+ \rightarrow \mu^+ + \nu_\mu \]
Ora però i fermioni hanno elicità invertita. In particolare, il neutrino che inizialmente era sinistrorso diventa destrorso.
Poiché i neutrini destrorsi non partecipano all’interazione debole, il processo ottenuto non è fisicamente osservato.
Questo mostra che la simmetria di parità P è violata.
2] Coniugazione di carica (C)
Per studiare la trasformazione combinata CP, applico ora la coniugazione di carica C al processo ottenuto dopo l’azione di P.
\[ \pi^+ \rightarrow \mu^+ + \nu_\mu \]
L'operazione C scambia particelle e antiparticelle:
- \( \pi^+ \leftrightarrow \pi^- \)
- \( \mu^+ \leftrightarrow \mu^- \)
- \( \nu_\mu \leftrightarrow \bar\nu_\mu \)
Applicando C ottiengo il processo:
\[ C( \pi^+ ) \rightarrow C( \mu^+ ) + C( \nu_\mu ) \]
\[ \pi^- \rightarrow \mu^- + \bar\nu_\mu \]
La coniugazione di carica non inverte l’elicità.
Di conseguenza, l’antineutrino nel processo finale risulta destrorso, come richiesto dall’interazione debole. Il processo ottenuto è quindi fisicamente permesso e soddisfa la simmetria CP.
Infatti, corrisponde al decadimento reale del pione negativo, che è effettivamente osservato in natura.
Questo esempio mostra che, sebbene la simmetria di parità P (e anche la simmetria C) sia violata nelle interazioni deboli, l’azione combinata CP può trasformare un processo reale in un altro processo reale.
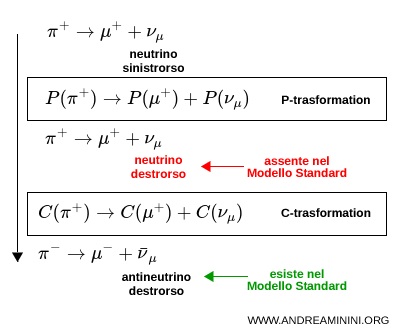
Nota. L’operazione P da sola ribalta l’elicità, producendo neutrini con chiralità non ammessa, quindi non è una simmetria valida. L’operazione C da sola scambia particelle e antiparticelle, ma non modifica l’elicità, e quindi non funziona da sola. L’operazione combinata CP, invece, scambia particelle e antiparticelle e contemporaneamente ribalta l’elicità, riportando in molti casi il processo all’interno della classe di fenomeni effettivamente osservati.
In questo senso, la simmetria CP può essere soddisfatta anche quando le singole simmetrie C e P sono violate, senza modificare la fisica dei fenomeni osservati.
E così via.
