La costante di struttura fine

La costante di struttura fine, indicata con il simbolo $ \alpha $, è un numero puro e adimensionale $ \alpha = 1/137 $ che misura l'intensità dell’interazione elettromagnetica tra particelle cariche. È definita come: \[ \alpha = \frac{e^2}{4 \pi \varepsilon_0 \hbar c} \]

Dove:

• \( e = 1,602176634 \cdot 10^{-19} C \) è la carica elementare
• \( \varepsilon_0 \) è la permittività elettrica del vuoto
• \( \hbar = \frac{h}{2 \pi} \) è la costante di Planck ridotta (\( h/2\pi \))
• \( c \) è la velocità della luce nel vuoto

Il suo valore numerico è:

\[ \alpha \approx \frac{1}{137.035999177} \]

La particolarità di α è che non dipende da alcuna unità di misura, quindi è un parametro fondamentale e universale.

Nota. Agli inizi del Novecento, gli scienziati studiavano la luce emessa dagli atomi. Si aspettavano righe singole (cioè frequenze precise), ma ne vedevano più di una, molto vicine tra loro. Questo fenomeno fu chiamato struttura fine. Il fisico Arnold Sommerfeld trovò la spiegazione nel 1916: gli orbitali degli elettroni sono più complicati del previsto. Con l’aiuto della relatività, scoprì che esistevano piccole differenze di energia tra sottolivelli. Per descriverle, introdusse una nuova costante: $ \alpha $.

Nella vecchia teoria di Bohr, $ \alpha $ coincide con il rapporto tra la velocità dell’elettrone nel primo orbitale dell’idrogeno e la velocità della luce. 

Perché α è così importante?

La costante di struttura fine α è fondamentale per la fisica dell’universo,  spiega perché la materia è stabile.

In particolare, α stabilisce la forza con cui elettroni e protoni si legano, quindi determina la dimensione degli atomi, la stabilità dei legami chimici, l’intera struttura della chimica e persino i processi che avvengono all’interno delle stelle.

Nella teoria moderna dell’elettromagnetismo (QED), la costante $ \alpha $ misura quanto è forte il legame tra un elettrone e un fotone.

Cosa accadrebe se $ \alpha $ fosse più grande?

Se \( \alpha \) aumentasse, ad esempio fino a \( 1/110 \), l’attrazione elettrica tra il nucleo e gli elettroni diventerebbe più intensa.

Questo costringerebbe gli elettroni a orbitare più vicino al nucleo, rendendo gli atomi significativamente più piccoli e i legami chimici molto più forti.

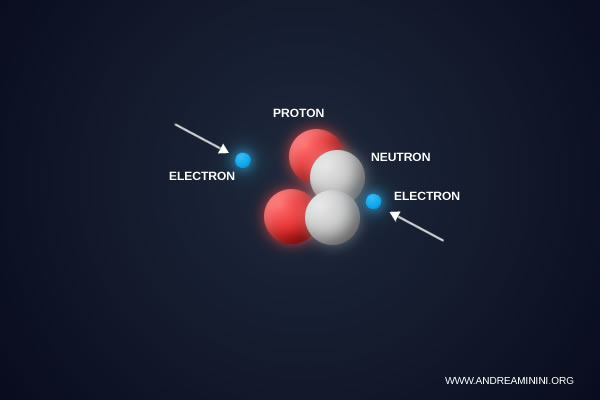
Inoltre, un valore più alto di \( \alpha \) aumenterebbe anche la repulsione elettrica tra i protoni nel nucleo. Di conseguenza molti nuclei diventerebbero instabili, perché la forza nucleare forte non basterebbe più a tenerli uniti. Alcuni elementi chimici non si formerebbero affatto.

Esempio.In questo scenario con i legami chimici risulterebbero molto più forti e rigidi. Le molecole cambierebbero con più difficoltà. Quindi, le reazioni chimiche diventerebbero più rare, alterando profondamente la chimica come la conosciamo. Nelle cellule, le reazioni chimiche avvengono perché le molecole si rompono e si riformano. Se gli atomi fossero troppo legati, niente si romperebbe. La chimica della vita sarebbe bloccata.

E se $ \alpha $ fosse più piccolo?

Se \( \alpha \) diminuisse, ad esempio fino a \( 1/200 \), l’attrazione elettrica tra nucleo ed elettroni sarebbe più debole.

Gli elettroni orbiterebbero a distanze maggiori, rendendo gli atomi più grandi e molto meno stabili, perché gli elettroni potrebbero essere strappati via con maggiore facilità.

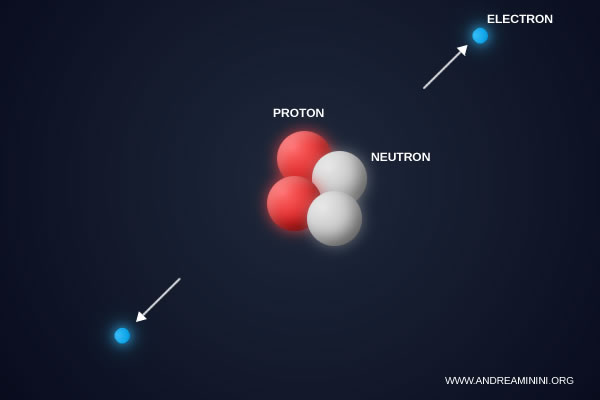
In queste condizioni anche i legami chimici risulterebbero estremamente deboli. La maggior parte delle molecole non riuscirebbe a rimanere unita, e la chimica organica sarebbe impossibile.

Esempio. Le molecole come il DNA, le proteine, l’acqua non si formerebbero se $ \alpha $ fosse troppo basso. Non ci sarebbe più la base per la vita. Anche le stelle non potrebbero produrre elementi come carbonio e ossigeno, essenziali per la vita, perché cambierebbero le probabilità di risonanza nelle reazioni nucleari (come il triplo alfa) da cui nasce il carbonio. Con un α troppo diverso, quelle reazioni non avrebbero più il bilanciamento fine necessario.

La costante α e la probabilità con cui un elettrone interagisce con i fotoni

In meccanica quantistica un elettrone non interagisce con la luce in modo continuo.

Le interazioni avvengono attraverso singoli eventi: un elettrone può emettere un fotone o assorbirlo, cambiando il proprio stato energetico.

Questi processi non sono automatici, hanno una certa probabilità di verificarsi, e la costante di struttura fine \( \alpha \) stabilisce quanto sono probabili.

Se \( \alpha \) fosse molto più grande, gli elettroni emetterebbero e assorbirebbero fotoni con estrema facilità, rendendo l’elettromagnetismo molto più intenso. Viceversa, se fosse più piccolo, gli scambi sarebbero rari e deboli.

Nota. È importante precisare che \( \alpha \) non è una probabilità diretta, ma il numero che determina la forza dell’interazione elettrone-fotone. Nella teoria quantistica dei campi la “forza” con cui un elettrone interagisce con la luce è proporzionale a \( \sqrt{\alpha} \), mentre le probabilità dei processi risultano proporzionali ad \( \alpha \approx 1/137 \). Per questo si dice, in modo semplificato, che 1/137 misura “quanto è facile” per un elettrone scambiare un fotone.

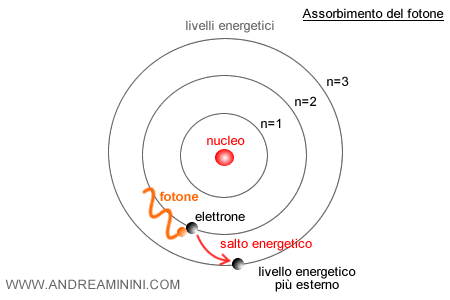
Ad esempio, in un atomo un elettrone occupa un livello energetico ben definito.

Per passare a un livello più alto deve assorbire un fotone con l’energia giusta.

La probabilità che questo assorbimento avvenga è governata proprio da \( \alpha \): più grande è α, più l’elettrone “sente” il campo elettromagnetico e più facilmente compie il salto orbitale.

Il processo inverso avviene quando un elettrone torna a un livello più basso: in quel caso emette un fotone.

Anche qui, la probabilità dell’emissione è proporzionale ad \( \alpha \).

Quindi, un valore piccolo come 1/137 rende questi salti energetici possibili ma non eccessivamente frequenti, ed è proprio questo equilibrio che permette la stabilità degli atomi e degli spettri di emissione che osserviamo negli esperimenti.

Note

Alcune note aggiuntive sulla costante di struttura fine

• Il valore di $ \alpha $ cambia con l’energia
  Anche se si chiama “costante”, il valore di $ \alpha $ cambia leggermente se cambia l’energia del fenomeno che osserviamo. Alle alte energie, $ \alpha $ diventa un po’ più grande. Ad esempio, a riposo (energia bassa) il suo valore è all'incirca $$ \alpha \approx \frac{1}{137} $$ A energia alta, come nei grandi acceleratori di particelle, il suo valore è $$ \alpha \approx \frac{1}{127} $$
• Multiverso
  Secondo alcune ipotesi del multiverso esisterebbero molti universi con valori diversi di α e il nostro sarebbe semplicemente uno di quelli in cui questo valore assume quello “giusto” ( $ \alpha \approx \frac{1}{137} $ ) per permettere l’esistenza della materia stabile. Tuttavia, l’idea del multiverso resta comunque un’ipotesi speculativa, non verificabile sperimentalmente, quindi non si può considerare una spiegazione definitiva del perché α abbia proprio questo valore.
• Il principio antropico
  Alcuni scienziati pensano che $ \alpha $ abbia proprio il valore giusto per permettere la vita. Secondo il principio antropico osserviamo il valore α = 1/137 perché se fosse diverso, non potremmo essere qui a osservarlo.

  Nota. Il problema è che il principio antropico, preso da solo, non spiega davvero perché α abbia quel valore, si limita a dire che noi possiamo osservarlo solo negli universi in cui è permessa la nostra esistenza, il che rischia di trasformarlo più in una constatazione tautologica che in una spiegazione fisica.

• La costante $ \alpha $ come linguaggio universale
  Poiché la costante di struttura fine $ \alpha = \frac{1}{137} $ è un numero puro (privo di unità di misura) e identico ovunque nell’universo, qualunque civiltà in grado di studiare l’elettromagnetismo la ricaverebbe dallo stesso calcolo. In questo senso potrebbe costituire un riferimento comune tra specie intelligenti, una sorta di linguaggio universale basato sulla fisica.
  
• La controversia sul valore costante di $ \alpha $ nel tempo e nello spazio
  Subito dopo il Big Bang il valore di $ \alpha $ sembra essersi stabilito molto rapidamente a $ \alpha = \frac{1}{137} $ e, per quanto ne sappiamo oggi, non ci sono evidenze che sia mai cambiato nel corso della storia dell’universo. Negli ultimi decenni diversi gruppi di ricerca hanno provato a verificare se $ \alpha $ sia davvero costante nel tempo e nello spazio. Nel 1999, un gruppo di scienziati analizzò la luce proveniente da quasar lontanissimi, trovando un piccolo cambiamento nel valore di α rispetto a oggi: $$ \frac{\Delta \alpha}{\alpha} = (-5.7 \pm 1.0) \times 10^{-6} $$ Quindi, secondo questa analisi, la costante di struttura fine potrebbe variare nello spazio e nel tempo. Tuttavia altri studi, basati su osservazioni e metodi diversi, non hanno confermato questo risultato. Ad oggi la questione rimane aperta: non ci sono prove conclusive né di una variazione né della sua assoluta immutabilità.

E così via.