I diagrammi di Young nella simmetria SU(3)

I diagrammi di Young sono uno strumento grafico che mi permette di rappresentare in modo semplice le rappresentazioni del gruppo SU(3) e di calcolare come si combinano tra loro.

Nella fisica delle particelle, la simmetria SU(3) descrive la simmetria di sapore dei quark up, down e strange ( u,d,s ).

I diagrammi di Young servono a classificare i mesoni, i barioni e le multiplette di particelle in base alle loro proprietà di simmetria.

Cos’è un diagramma di Young

Un diagramma di Young è formato da caselle disposte in righe, allineate a sinistra, con lunghezza non crescente dall’alto verso il basso.

La rappresentazione fondamentale di SU(3) è indicata con un diagramma con una sola casella che ha dimensione $ 3 $ e fisicamente corrisponde al tripletto dei quark \(  \{ u,d,s \} \).

Ad esempio, una sola casella (1), due caselle in riga (2), due caselle in colonna (1,1), due caselle sopra e una sotto (2,1), ecc.

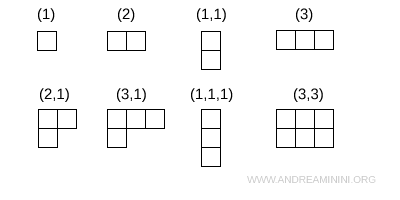
Ogni diagramma rappresenta una classe di simmetria degli indici di una rappresentazione tensoriale.

Regole fondamentali per SU(3)

Nel caso del gruppo SU(3) valgono alcune regole essenziali.

1. Ogni casella rappresenta un indice che trasforma come la rappresentazione fondamentale \( 3 = \{ u,d,s \} \).
2. Le caselle sulla stessa riga indicano la simmetrizzazione degli indici.
3. Le caselle sulla stessa colonna indicano l'antisimmetrizzazione.
4. Il diagramma deve avere righe di lunghezza non crescente dall’alto verso il basso.
5. In SU(3) non possono esserci più di 3 righe, perché l’antisimmetrizzazione di quattro indici è nulla. Questa ultima regola è cruciale perché limita automaticamente le rappresentazioni ammissibili.
6. Prodotto tensoriale
   Nel prodotto tensoriale (es. $ 6 \otimes 3 $), le caselle del secondo fattore si aggiungono una alla volta al diagramma del primo, generando tutti i diagrammi possibili che rispettano le regole di Young. Ogni disposizione che viola una regola deve essere scartata. Se, durante l’aggiunta, una casella non ha più posizioni ammesse, quel canale si chiude.
   • Antisimmetria delle colonne
     Nel prodotto tensoriale le caselle appartenenti a una colonna antisimmetrica
     1] non possono mai stare tutte sulla stessa riga
     2] possono stare tutte nella stessa colonna solo se prolungano una colonna già esistente nel diagramma iniziale 
   • Controllo finale delle dimensioni
     La somma delle dimensioni dei diagrammi ammessi deve coincidere con la dimensione del prodotto tensoriale. Ad esempio, per $ 6 \otimes 3 $ ci sono $ 6 \times 3 = 18 $ stati, quindi anche la somma delle rappresentazioni deve essere uguale a 18 (es. $ 15 \oplus 3 $ ).  Se alcuni canali si chiudono e manca una parte della dimensione totale, il “resto” si ottiene per differenza ed è identificato con la rappresentazione compatibile.

Perché i diagrammi di Young sono così utili? I diagrammi di Young permettono di visualizzare le simmetrie, individuare le rappresentazioni ammesse e capire quali combinazioni di quark sono possibili, senza lunghi calcoli. In questo modo l’algebra di SU(3) viene tradotta in una geometria discreta immediata. I diagrammi di Young non stabiliscono quali particelle esistono, ma quali simmetrie sono consentite. È SU(3) a imporre la struttura, i diagrammi sono solo il linguaggio più diretto per leggerla.

Le combinazioni di multiplette possibili

Per calcolare le combinazioni possibili di multiplette in un diagramma di Young nella simmetria SU(3) si usa questa formula:

\[ \dim = \prod_{\text{caselle}} \ \frac{N + c - r}{h} \]

Dove

• \( N \) è la dimensione della rappresentazione fondamentale del gruppo. Ad esempio, per SU(2) è N = 2, per SU(3) è N=3, per SU(4) è N=4, ecc.
• \( r \) è l'indice di riga della casella nel diagramma di Young. Si conta dall’alto verso il basso, partendo da 0.
• \( c \) è l'indice di colonna della casella nel diagramma di Young. Si conta da sinistra verso destra, partendo da 0.
• \( h \) è la lunghezza dell'uncino (hook length) della casella: \[ h = (\text{numero di caselle a destra}) + (\text{numero di caselle sotto}) + 1 \] Dove \( +1 \) è la casella stessa.

Il prodotto va fatto su tutte le caselle del diagramma di Young.

Nota. La componente $ (c - r) $ dipende solo dalla posizione della casella. La componente \( h \) dipende solo dalla forma del diagramma. La formula vale per ogni diagramma di Young in SU(N) e non richiede correzioni successive

Un esempio pratico

Combinazione di due quark: \( 3 \otimes 3 \)

Considero il prodotto tensoriale di due rappresentazioni fondamentali \( 3 = \{ u,d,s \} \).

$$ 3 \otimes 3 $$

Rappresento $ 3 $ con un quadrato che ha indici \(  \{ u,d,s \} \)

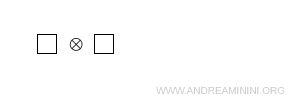
Per svolgere questo calcolo con il diagramma di Young, aggiungo la seconda casella alla prima, rispettando le regole. Ho due possibilità:

1. Due caselle in riga
   Le caselle sono in riga, quindi questa rappresentazione è simmetrica e corrisponde alla rappresentazione \( 6 \).
   
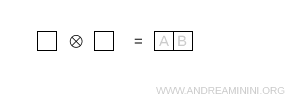   Nota. Per trovare la dimensione calcolo il prodotto tra i valori di ogni casella usando la formula \[ \dim = \prod_{\text{caselle}} \ \frac{N + c - r}{h} \] In questo caso N=3 perché siamo in SU(3).
   

   • Casella A. L'indice di riga è $ r=0 $, l'indice di colonna è $ c=0 $, c'è una sola casella a destra e zero in basso, quindi $ h=1+0+1=2 $ (destra+sotto+1).  $$ \frac{N + c - r}{h}  = \frac{3 + 0 - 0}{2} = \frac{3}{2} $$
   • Casella B. L'indice di riga è $ r=0 $, l'indice di colonna è $ c=1 $, non ci sono caselle né a destra, né sotto, quindi $ h=0+0+1=1 $ (destra+sotto+1).  $$ \frac{N + c - r}{h}  = \frac{3 + 1 - 0}{1} = 4 $$

   Il prodotto tra i valori delle caselle è la dimensione $$ dim = \frac{3}{2} \cdot 4 = 6 $$ Essendo una combinazione simmetrica, in quanto le caselle sono disposte in orizzontale, corrisponde alla rappresentazione $ 6 $
2. Due caselle in colonna
   Le caselle sono in colonna, quindi questa rappresentazione è antisimmetrica e corrisponde alla rappresentazione \( \bar{3} \).
   
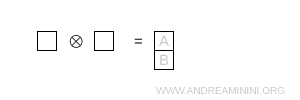   Nota. Anche in questo caso calcolo il prodotto tra i valori di ogni casella usando la formula \[ \dim = \prod_{\text{caselle}} \ \frac{N + c - r}{h} \] con N=3 perché siamo in SU(3).
   

   • Casella A. L'indice di riga è $ r=0 $, l'indice di colonna è $ c=0 $, non ci sono caselle a destra e c'è una sola casella in basso, quindi $ h=0+1+1=2 $ (destra+sotto+1).  $$ \frac{N + c - r}{h}  = \frac{3 + 0 - 0}{2} = \frac{3}{2} $$
   • Casella B. L'indice di riga è $ r=1 $, l'indice di colonna è $ c=0 $, non ci sono caselle né a destra, né sotto, quindi $ h=0+0+1=1 $ (destra+sotto+1).  $$ \frac{N + c - r}{h}  = \frac{3 + 0 - 1}{1} = 2 $$

   Il prodotto tra i valori delle caselle è la dimensione $$ dim = \frac{3}{2} \cdot 2 = 3 $$ Poiché la forma delle caselle indica una combinazione antisimmetrica, in quanto le caselle sono in verticale, corrisponde alla rappresentazione \( \bar 3 \).

Quindi, il risultato è

\[ 3 \otimes 3 = 6 \oplus \bar{3} \]

Fisicamente, questo vuol dire che ci sono 6 coppie simmetriche di quark e 3 coppie antisimmetriche di quark.

Nota. Questo coincide con la realtà fisica. Una coppia di quark è simmetrica quando sostituendo la posizione di un quark non cambia lo stato. E' antisimmetrica quando lo stato è lo stesso ma cambia il segno. Considerando 3 quark ( \( u,d,s \) ) ci sono 6 coppie simmetriche. \[ uu \xrightarrow{\text{scambio}} uu  \] \[ dd \xrightarrow{\text{scambio}} dd \] \[ ss \xrightarrow{\text{scambio}} ss \] \[ ud+du \xrightarrow{\text{scambio}} du+ud = ud+du \] \[ us+su \xrightarrow{\text{scambio}} su+us = us+su \] \[ ds+sd \xrightarrow{\text{scambio}} sd+ds =  ds+sd \] E 3 coppie antisimmetriche. \[ ud-du \xrightarrow{\text{scambio}} du-ud = - (ud - du) \] \[ us-su \xrightarrow{\text{scambio}} su-us = - (us - su) \] \[ ds-sd \xrightarrow{\text{scambio}} sd-ds = - (ds - sd) \]

Combinazione di tre quark: \( 3 \otimes 3 \otimes 3 \)

Questo è il caso fondamentale per i barioni.

$$ 3 \otimes 3 \otimes 3 $$

Partendo dal risultato precedente $ 3 \otimes 3 $ (due caselle in orizzontale o in verticale), aggiungo un’altra casella. I diagrammi di Young ammessi sono:

1. Tre caselle in riga
   E' un caso completamente simmetrico e rappresenta il decupletto \( 10 \)
   
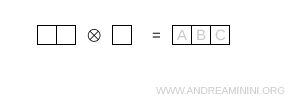   Nota. Calcolo il prodotto tra i valori di ogni casella usando la formula \[ \dim = \prod_{\text{caselle}} \ \frac{N + c - r}{h} \] In questo caso N=3.
   

   • Casella A. L'indice di riga è $ r=0 $, l'indice di colonna è $ c=0 $, ci sono due caselle a destra e zero in basso, quindi $ h=2+0+1=3 $ (destra+sotto+1).  $$ \frac{N + c - r}{h}  = \frac{3 + 0 - 0}{3} = \frac{3}{3} = 1 $$
   • Casella B. L'indice di riga è $ r=0 $, l'indice di colonna è $ c=1 $, c'è una casella a destra, nessuna casella sotto, né sotto, quindi $ h=1+0+1=2 $ (destra+sotto+1).  $$ \frac{N + c - r}{h}  = \frac{3 + 1 - 0}{2} = \frac{4}{2} = 2 $$
   • Casella C. L'indice di riga è $ r=0 $, l'indice di colonna è $ c=2 $, non ci sono caselle a destra, né sotto, quindi $ h=0+0+1=1 $ (destra+sotto+1).  $$ \frac{N + c - r}{h}  = \frac{3 + 2 - 0}{1} = 5  $$

   Il prodotto tra i valori delle caselle è la dimensione $$ dim = 1 \cdot 2 \cdot 5 = 10 $$ E' una combinazione simmetrica, in quanto le caselle sono disposte in orizzontale, e corrisponde alla rappresentazione $ 10 $ (decupletto).
2. Due caselle sopra e una sotto
   E' una simmetria mista e rappresenta l'ottetto \( 8 \)
   
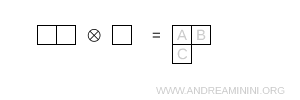   Nota. Di nuovo uso la formula \[ \dim = \prod_{\text{caselle}} \ \frac{N + c - r}{h} \] Sempre con N=3.
   

   • Casella A. L'indice di riga è $ r=0 $, l'indice di colonna è $ c=0 $, c'è una casella a destra e una sotto, quindi $ h=1+1+1=3 $ (destra+sotto+1).  $$ \frac{N + c - r}{h}  = \frac{3 + 0 - 0}{3} = \frac{3}{3} = 1 $$
   • Casella B. L'indice di riga è $ r=0 $, l'indice di colonna è $ c=1 $, non ci sono caselle né a destra, né sotto, quindi $ h=0+0+1=1 $ (destra+sotto+1).  $$ \frac{N + c - r}{h}  = \frac{3 + 1 - 0}{1} = 4 $$
   • Casella C. L'indice di riga è $ r=1 $, l'indice di colonna è $ c=0 $, non ci sono caselle a destra, né sotto, quindi $ h=0+0+1=1 $ (destra+sotto+1).  $$ \frac{N + c - r}{h}  = \frac{3 + 0 - 1}{1} = 2  $$

   Il prodotto tra i valori delle caselle è la dimensione $$ dim = 1 \cdot 4 \cdot 2 =8 $$ E' una combinazione mista e corrisponde alla rappresentazione $ 8 $ (decupletto).
3. Tre caselle in colonna
   E' un caso completamente antisimmetrico e rappresenta un singoletto \( 1 \).
   
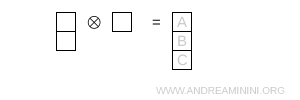   Nota. Uso di nuovo la formula con N=3 \[ \dim = \prod_{\text{caselle}} \ \frac{N + c - r}{h} \]
   

   • Casella A. L'indice di riga è $ r=0 $, l'indice di colonna è $ c=0 $, ci sono due caselle sotto e zero a destra, quindi $ h=0+2+1=3 $ (destra+sotto+1).  $$ \frac{N + c - r}{h}  = \frac{3 + 0 - 0}{3} = \frac{3}{3} = 1 $$
   • Casella B. L'indice di riga è $ r=1 $, l'indice di colonna è $ c=0 $,  c'è una casella sotto e zero a destra, quindi $ h=0+1+1=2 $ (destra+sotto+1).  $$ \frac{N + c - r}{h}  = \frac{3 + 0 - 1}{2} = \frac{2}{2} = 1 $$
   • Casella C. L'indice di riga è $ r=2 $, l'indice di colonna è $ c=0 $, non ci sono caselle a destra, né sotto, quindi $ h=0+0+1=1 $ (destra+sotto+1).  $$ \frac{N + c - r}{h}  = \frac{3 + 0 - 2}{1} = 1  $$

   Il prodotto tra i valori delle caselle è la dimensione $$ dim = 1 \cdot 1 \cdot 1 = 1 $$ In questo caso si tratta di un singoletto che si rappresenta sempre con $ 1 $ perché la rappresentazione 1-dimensionale è identica a se stessa $ \bar{1}=1 $.
4. Due caselle sopra e una sotto
   E' una simmetria mista e rappresenta l'ottetto \( 8 \)
   

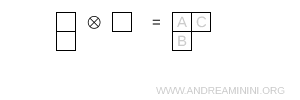
   Nota. Questa forma l'ho già calcolata in precedenza e so già che rappresenta l'ottetto ($ 8 $).

Quindi, il risultato finale è:

\[ 3 \otimes 3 \otimes 3 = 10 \oplus 8 \oplus 8 \oplus 1 \]

Queste sono esattamente le multiplette osservate sperimentalmente.

Nota. Ogni diagramma di Young non è solo un oggetto matematico, ma ha un significato fisico preciso.Il decupletto (10) descrive barioni completamente simmetrici, come le particelle \( \Delta \). L’ottetto (8) descrive barioni a simmetria mista, come nucleoni, \( \Sigma \), \( \Xi \).Il singoletto (1) rappresenta uno stato completamente antisimmetrico.

Combinazione di due quark: \( 3 \otimes \bar 3 \)

In questo esempio calcolo il prodotto tensoriale

$$ 3 \otimes \bar 3 $$

Rappresento $ 3 $ con una casella e $ \bar 3 $ con due caselle in colonna perché corrisponde alla combinazione antisimmetrica di due indici

Svolgo il calcolo con i diagrammi di Young aggiungendo la casella di \(3\) al diagramma di \( \bar 3 \). Le disposizioni ammesse sono due.

• Due caselle in riga e una in basso
  Questo diagramma è il tipo (2,1) e ha dimensione $ 8 $
  

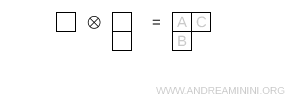
  Nota. Ho già svolto questo calcolo negli altri esempi precedenti. So già che rappresenta l'ottetto $ 8 $.

• Tre caselle in colonna
  Questo diagramma è il tipo (1,1,1) e ha dimensione 1.
  
  
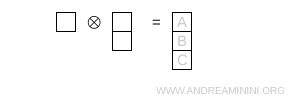
  Nota. Ho già svolto questo calcolo negli altri esempi precedenti. So già che rappresenta il singoletto $ 1 $.

Quindi il risultato della decomposizione è:

$$ 3 \otimes \bar 3 = 8 \oplus 1 $$

Anche questo risultato rispecchia la realtà sperimentale.

Combinazione \( 6 \otimes \bar 3 \)

Provo a calcolare il prodotto tensoriale

$$ 6 \otimes \bar 3 $$

Rappresento $ 6 $ con due caselle in orizzontale e $ \bar 3 $ con due caselle in colonna perché corrisponde alla combinazione antisimmetrica.

Svolgo il calcolo con i diagrammi di Young. Le disposizioni ammesse sono due.

• Tre caselle in riga e una in basso
  Questo diagramma è il tipo (3,1) e ha dimensione $ 15 $
  
  
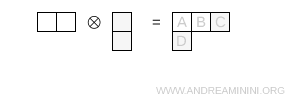
  Nota. Uso la formula \[ \dim = \prod_{\text{caselle}} \ \frac{N + c - r}{h} \] Sempre con N=3.
  

  • Casella A. L'indice di riga è $ r=0 $, l'indice di colonna è $ c=0 $, ci sono due caselle a destra e una sotto, quindi $ h=2+1+1=4 $ (destra+sotto+1).  $$ \frac{N + c - r}{h}  = \frac{3 + 0 - 0}{4} = \frac{3}{4}  $$
  • Casella B. L'indice di riga è $ r=0 $, l'indice di colonna è $ c=1 $, c'è una casella a destra e nessuna sotto, quindi $ h=1+0+1=2 $ (destra+sotto+1).  $$ \frac{N + c - r}{h}  = \frac{3 + 1 - 0}{2} = \frac{4}{2} = 2 $$
  • Casella C. L'indice di riga è $ r=0 $, l'indice di colonna è $ c=2 $, non ci sono caselle a destra, né sotto, quindi $ h=0+0+1=1 $ (destra+sotto+1).  $$ \frac{N + c - r}{h}  = \frac{3 + 2 - 0}{1} = 5  $$
  • Casella D. L'indice di riga è $ r=1 $, l'indice di colonna è $ c=0 $, non ci sono caselle a destra, né sotto, quindi $ h=0+0+1=1 $ (destra+sotto+1).  $$ \frac{N + c - r}{h}  = \frac{3 + 0 - 1}{1} = 2  $$

  Quindi, la dimensione $$ dim = \frac{3}{4} \cdot 2 \cdot 5 \cdot 2 =15 $$ E' una combinazione a simmetria mista.
• Non ci sono altre disposizioni ammesse
  Le due caselle della colonna antisimmetrica non posso aggiungerle entrambe sulla stessa riga, perché imporrei una simmetrizzazione incompatibile con l’antisimmetria. Non posso nemmeno aggiungerle entrambe in colonna, poiché nel diagramma iniziale non esiste una colonna da prolungare. Se aggiungo una sola casella sotto, la seconda non trova alcuna posizione ammessa e il canale di composizione si chiude.
  
  
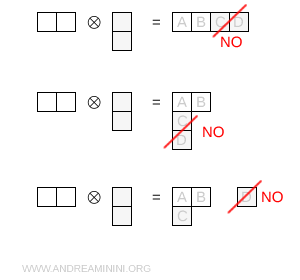
  Soluzione. In questo caso si determina la rappresentazione compatibile con il resto. La dimensione del prodotto tensoriale \( 6 \otimes \bar 3 \) è \( 6 \times 3 = 18 \), quindi il numero totale di stati deve essere 18. Finora ho trovato una rappresentazione di dimensione 15, per cui resta $$ 18 - 15 = 3 $$ Poiché \( 3 \) è una rappresentazione ammessa di SU(3), concludo che il termine mancante nella decomposizione è proprio \( 3 \).

Pertanto, il risultato della decomposizione è:

$$ 6 \otimes \bar 3 = 15 \oplus 3 $$

In questo modo i diagrammi permettono quindi di capire perché esistono certe particelle e non altre.

E così via.