Costante di accoppiamento
Nella fisica teorica la costante di accoppiamento (coupling constant) misura l’intensità di un'interazione tra particelle.
È un parametro che determina quanto fortemente due particelle interagiscono e si influenzano a causa di una determinata forza fondamentale.
In altre parole, più grande è la costante di accoppiamento, più forte è l’interazione tra le particelle.
- Una costante piccola comporta una interazione debole (es. QED: $\alpha \approx 1/137$). Questo permette il calcolo perturbativo e l'espansione in serie.
- Una costante grande implica una interazione forte (es. QCD a bassa energia: $\alpha_s \sim 1$). In questo caso il calcolo perturbativo è inaffidabile.
Cos'è il calcolo perturbativo? Il calcolo perturbativo è una tecnica matematica usata in fisica per semplificare un problema. Quando un problema è molto difficile ma l'interazione è debole, si può trattare l'interazione come una perturbazione di un problema più semplice (privo di interazione). Per questa ragione una costante di accoppiamento piccola consente il calcolo perturbativo.
Ecco alcuni esempi di costanti di accoppiamento nelle quattro forze fondamentali dell'universo.
| Interazione | Costante | Simbolo | Valore tipico |
|---|---|---|---|
| Elettromagnetica | Fine-structure constant | α | ≈ 1/137 |
| Forte (QCD) | Coupling forte | αs | Variabile: ≈ 0.1 - 1 |
| Debole | GF (di Fermi) | - | ≈ 1.166 × 10-5 GeV-2 |
| Gravitazionale (in unità naturali) | G | - | Estremamente debole |
La funzione beta
Nella teoria quantistica dei campi, le costanti di accoppiamento non sono realmente costanti, ma dipendono dalla scala di energia.
La costante di accoppiamento varia con l’energia (e quindi con la distanza) secondo la funzione beta.
Ad esempio, nella QED (elettrodinamica quantistica), la costante di accoppiamento elettromagnetico $ \alpha $ dipende dall’energia $ E $ alla quale avviene l’interazione:
$$ \alpha(E) \ne \alpha(0) \quad \text{(la carica cresce con l’energia)} $$
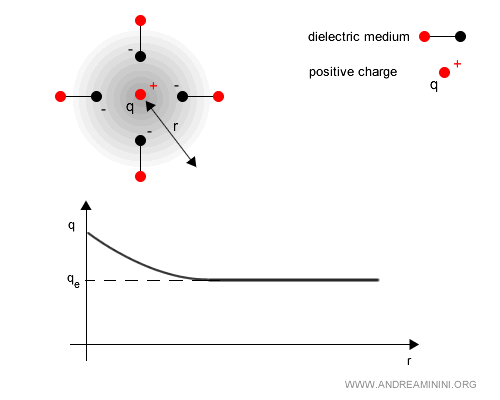
Questo fenomeno è noto come schermatura del vuoto: a causa delle fluttuazioni quantistiche, il vuoto si comporta come un mezzo dielettrico che "nasconde" parte della carica a basse energie (cioè su scale di lunghezza grandi).
Quindi a energie più alte (ossia a distanze più piccole), la schermatura è meno efficace e la carica effettiva cresce.
Esempio. Il vuoto quantistico si comporta come un mezzo dielettrico perché le fluttuazioni quantistiche generano un effetto di polarizzazione, dovuto alla presenza di coppie virtuali elettrone-positrone. Ad esempio, in presenza di una carica positiva $q$, le componenti negative delle coppie virtuali vengono attirate verso la carica, mentre quelle positive vengono respinte. Questo provoca una ridistribuzione del campo elettrico che tende a schermare la carica a grande distanza. Il risultato è che, man mano che ci si allontana, la carica effettiva misurata $q_e(r)$ risulta inferiore alla carica reale $q$.
Viceversa, nella QCD (cromodinamica quantistica), la costante di accoppiamento forte $\alpha_s$ diminuisce con l’aumentare dell’energia o del quadrato del momento trasferito $Q^2$:
$$ \alpha_s(Q^2) \downarrow \text{ con } Q^2 \uparrow \quad \text{(libertà asintotica)} $$
Questo comportamento è chiamato anti-schermatura ed è causato dalle autointerazioni tra gluoni, che portano carica di colore (a differenza dei fotoni che sono neutri).
L'effetto netto è che, a distanze molto piccole (cioè ad alte energie), l’interazione tra i quark si indebolisce, e i quark si comportano quasi come particelle libere all’interno di un adrone (come un protone o un neutrone). Questo fenomeno è detto libertà asintotica.
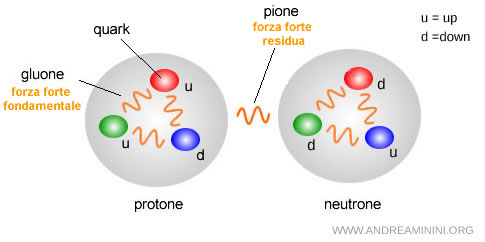
Tuttavia, quando un quark tenta di allontanarsi dal resto dell'adrone, la forza di interazione con il campo di colore aumenta rapidamente, fino a diventare così intensa da impedirne la separazione: questo fenomeno è noto come confinamento del quark.
Nota. È un concetto cruciale per comprendere fenomeni come la libertà asintotica, la schermatura del vuoto, e la struttura delle interazioni fondamentali. Ad esempio, questo è il motivo per cui nei collisionatori ad alta energia, come il LHC, i quark sembrano non interagire fortemente, anche se lo fanno a scale più grandi, dove il confinamento li lega all’interno degli adroni.
Note
Alcune note a margine e osservazioni personali.
- In una teoria di gauge (es. QED o QCD), la costante di accoppiamento $g$ compare nella Lagrangiana: $$ \mathcal{L}_{\text{int}} = g \, \bar{\psi} \gamma^\mu A_\mu \psi $$ Dove $g$ è la costante di accoppiamento, $A_\mu$ è il campo mediatore (es. fotone, gluone) e $\psi$ è il campo di materia (es. elettrone, quark)
E così via.
