Lo spin in meccanica quantistica
Lo spin è un numero quantico associato a ogni particella elementare. Contribuisce, insieme ad altri numeri quantici (energia, momento angolare orbitale, ecc.), a determinare lo stato quantico completo di un sistema fisico.
Non è una quantità derivata dal moto nello spazio, ma una proprietà intrinseca della particella stessa.
E' una forma di momento angolare. Lo spin ha le stesse dimensioni fisiche del momento angolare classico (kg·m²/s) e può essere trattato matematicamente in modo simile.
Tuttavia, non rappresenta la rotazione meccanica di un corpo attorno a un asse.
Esempio. L’elettrone è trattato come un'entità puntiforme, priva di dimensioni spaziali definite. Di conseguenza, non possiede un vero "asse di rotazione". Fin dalla scoperta dell’elettrone è stata esclusa l’idea che potesse essere una piccola sfera che ruota su se stessa, perché un oggetto così minuscolo dovrebbe ruotare più veloce della luce per generare il momento angolare, in violazione diretta della relatività speciale.
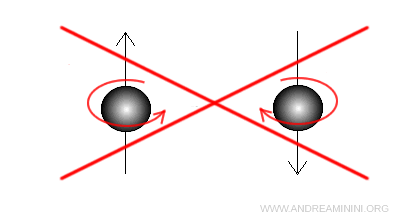
Inoltre, una carica elettrica distribuita su una sfera in rotazione emetterebbe continuamente radiazione elettromagnetica, cosa che non avviene. Per questo lo spin non può essere interpretato come una rotazione classica, ma è una proprietà quantistica intrinseca delle particelle senza alcuna analogia con il mondo macroscopico che osserviamo.
Lo spin può assumere valori discreti (valori quantizzati). Questi valori sono multipli interi o seminteri di $\hbar/2$, dove $\hbar$ è la costante di Planck ridotta.
$$ s = 0,\ \tfrac{1}{2},\ 1,\ \tfrac{3}{2},\ 2,\ \tfrac{5}{2},\ \dots $$
In base allo spin possiamo distinguere due categorie di particelle elementari:
- Le particelle con spin intero (0, 1, 2, …) sono dette bosoni (es. fotone, gluone).
- Le particelle con spin semintero ($\frac{1}{2}$, $\frac{3}{2}$, …) sono dette fermioni (es. elettrone, protone, neutrino).
Le particelle con spin semintero $ \frac{1}{2} $ rivestono un ruolo fondamentale perché includono le principali particelle elementari che costituiscono l'atomo e la materia (es. protoni, neutroni, elettroni).
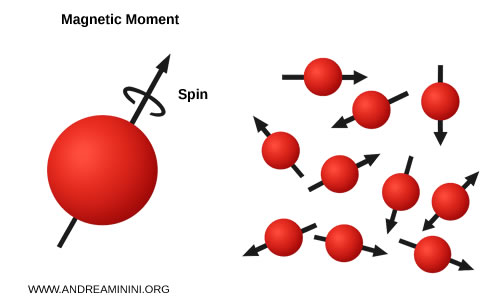
Ad esempio, lo spin $\frac{1}{2}$ dell’elettrone implica che esistono solo due stati di spin rispetto a una direzione scelta:
- “su” (up): $+\frac{1}{2}$
- "giù" (down): $-\frac{1}{2}$.
Per particelle con spin semintero, la rappresentazione matematica dello spin non è un vettore classico tridimensionale, ma un spinore.
Gli spinori sono oggetti a due componenti che si trasformano in modo non convenzionale sotto rotazioni.
In particolare, una rotazione di 360° non riporta uno spinore al suo stato iniziale, bensì nello stato opposto: serve una rotazione di 720°. Questo comportamento non ha analoghi classici.
Ecco una rappresentazione didattica di uno spinore su un nastro di Möbius. Dopo una rotazione di 360° la freccia si trova nel verso opposto.
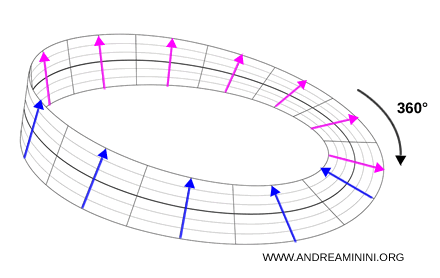
Serve un'altra rotazione per riportarla nel verso iniziale.
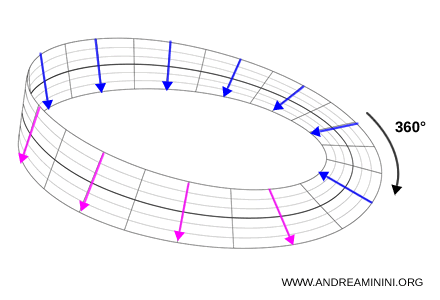
Ad esempio, nel formalismo di Pauli lo spin di una particella con spin 1/2 è descritto da un vettore a due componenti:
$$ \chi = \begin{pmatrix} \alpha \\ \beta \end{pmatrix} $$
Dove $\alpha$ e $\beta$ sono numeri complessi che determinano le probabilità di trovare la particella con spin "su" o "giù".
Nota. Quando si ruota un sistema di riferimento, anche lo spinore deve trasformarsi di conseguenza secondo una legge di rotazione specifica. $$ \begin{pmatrix} \alpha' \\ \beta' \end{pmatrix} = U(\theta) \begin{pmatrix} \alpha \\ \beta \end{pmatrix} $$ Dove \( U(\theta) \) è una matrice \( 2 \times 2 \) $$ U(\theta) = e^{- i \theta \cdot \sigma /2} $$ Il vettore \( \theta \) punta lungo l’asse di rotazione e la sua magnitudine è l’angolo della rotazione, nel senso della mano destra, attorno a quell’asse.
Qual è la differenza tra le rappresentazioni di spin 1 e 1/2?
La rappresentazione matematica delle particelle dipende dal valore del loro spin.
- Le particelle di spin 1 (bosoni vettoriali come il fotone) sono descritte da vettori a tre componenti nello spazio fisico, le cui rotazioni sono rappresentate da matrici \( 3 \times 3 \) appartenenti al gruppo \( SO(3) \), cioè il gruppo delle rotazioni ordinarie nello spazio tridimensionale.
- Le particelle di spin \( \tfrac{1}{2} \) sono invece descritte da spinori a due componenti. Le loro rotazioni non appartengono a \( SO(3) \) ma al gruppo \( SU(2) \), rappresentato da matrici \( 2 \times 2 \). Il gruppo \( SU(2) \) è la “doppia copertura” di \( SO(3) \), cioè la struttura matematica che spiega perché uno spinore torna allo stesso stato iniziale dopo una rotazione di \( 720^\circ \) e non dopo \( 360^\circ \). Un comportamento che non ha alcun equivalente nella meccanica classica.

Nota. Questa distinzione tra rappresentazioni \( 3 \times 3 \) di \( SO(3) \) e rappresentazioni \( 2 \times 2 \) di \( SU(2) \) è ciò che differenzia in modo netto lo spin classico (intero) dallo spin quantistico semintero.
- Le particelle di spin \( \tfrac{3}{2} \) sono descritte da oggetti a quattro componenti, che si trasformano secondo la rappresentazione quadrimensionale del gruppo \( SU(2) \). Come per gli altri casi di spin semintero, anche queste trasformazioni richiedono matrici diverse da quelle di \( SO(3) \) e presentano lo stesso comportamento tipico degli spinori, privo di analoghi nella meccanica classica.
In generale si può dire che:
- Lo spin 0 è uno scalare (dimensione 1)
- Lo spin \( \tfrac{1}{2} \) è uno spinore (dimensione 2)
- Lo spin 1 è un vettore (dimensione 3)
- Lo spin \( \tfrac{3}{2} \) è uno spinore esteso (dimensione 4)
Lo spin nella teoria delle particelle
In origine lo spin venne introdotto nella meccanica quantistica non relativistica per spiegare dati sperimentali, come la struttura fine degli spettri atomici o l’effetto Zeeman.
Nella meccanica quantistica relativistica, invece, lo spin emerge nell'equazione di Dirac che descrive il moto relativistico dell’elettrone e prevede l’esistenza dello spin $\frac{1}{2}$ e dei relativi stati.
Questa equazione fornisce anche una spiegazione teorica del momento magnetico anomalo dell’elettrone, osservato sperimentalmente. Spiega alcuni fenomeni fisici come:
- L'esclusione di Pauli: due fermioni non possono occupare lo stesso stato quantico, proprio grazie alla presenza dello spin.
- Proprietà statistiche delle particelle: le particelle con spin intero seguono la statistica di Bose-Einstein, mentre quelle con spin semintero seguono la statistica di Fermi-Dirac.
- Magnetismo: lo spin contribuisce a spiegare anche ai momenti magnetici delle particelle.
In conclusione, lo spin è un esempio emblematico di proprietà quantistiche che non hanno un corrispettivo classico.
Nasce da motivazioni sperimentali, ma trova la sua giustificazione teorica completa solo nel contesto relativistico.
Il suo comportamento è descritto dagli spinori e apre la strada alla comprensione delle interazioni fondamentali e delle proprietà statistiche delle particelle.
E così via.
