Particelle Sigma

Le particelle Sigma, indicate con la lettera greca $ \Sigma $, sono barioni formati da tre quark e appartengono alla famiglia delle particelle soggette all’interazione forte. Si distinguono per la presenza di un quark strange (s), che conferisce loro una proprietà detta stranezza.

Le particelle Σ sono costituite da tre quark:

• $ \Sigma^+ = uus $
• $ \Sigma^0 = uds $
• $ \Sigma^- = dds $

In tutti i casi è presente un quark strange (s), mentre gli altri due sono combinazioni di quark up (u) e down (d).

La carica elettrica

La carica elettrica deriva dalla somma delle cariche dei singoli quark sapendo che:

• $ q(u) = +2/3 $
• $ q(d) = -1/3 $
• $ q(s) = -1/3 $

Pertanto le cariche delle particelle sono

• $ q ( \Sigma^+ ) = +1 $
• $ q ( \Sigma^0 ) = 0 $
• $ q ( \Sigma^- ) = -1 $

Ad esempio, la particella $ \Sigma^+ $ è composta da due quark up e uno strange (uus), quindi la carica elettrica è: $$ q ( \Sigma^+ ) = q(u) + q(u) + q(s) = \frac{2}{3} + \frac{2}{3} - \frac{1}{3} = \frac{2+2-1}{3} = \frac{3}{3} = +1 $$La particella $ \Sigma^0 $ è composta da un quark up, un down e uno strange (uds), la sua carica elettrica è: $$ q ( \Sigma^0 ) = q(u) + q(d) + q(s) = \frac{2}{3} - \frac{1}{3} - \frac{1}{3} = \frac{2-1-1}{3} = \frac{0}{3} = 0 $$La particella $ \Sigma^- $ è composta da due quark down e uno strange (dds), la sua carica elettrica è: $$ q ( \Sigma^- ) = q(d) + q(d) + q(s) = - \frac{1}{3} - \frac{1}{3} - \frac{1}{3} = \frac{-1-1-1}{3} = \frac{-3}{3} = -1 $$ 

Isospin delle particelle Σ

Le particelle Σ hanno isospin totale pari a 1.

Questo accade perché l’isospin è determinato solo dai quark u e d, mentre il quark strange non contribuisce all’isospin.

I due quark u e d si combinano in uno stato simmetrico, dando un isospin totale:

$$ I = 1 $$

Spigazione.I quark $ u $ e $ d $ formano un doppietto di isospin, mentre il quark s non partecipa all’isospin e quindi non viene considerato in questa combinazione. Sia il quark up sia il quark down hanno isospin \( \tfrac12 \) con proiezioni: $$ I_3(u) = +\frac{1}{2} $$ $$ I_3(d) = -\frac{1}{2} $$ La matematica del gruppo SU(2) impone che la combinazione di due isospin \( \tfrac12 \) dia luogo solo a due possibilità, secondo la stessa regola dell’addizione dei momenti angolari: \[ \frac{1}{2} \otimes \frac{1}{2} = [ \frac{1}{2} + \frac{1}{2} ] \oplus [ \frac{1}{2} - \frac{1}{2} ] = 1 \oplus 0 \] Cioè, uno stato simmetrico con \( I = 1 \) e uno stato antisimmetrico con \( I = 0 \). Lo stato simmetrico con $ I = 1 $ forma un tripletto che corrisponde agli stati della particella Σ. \[  \begin{aligned} |1,+1\rangle &= uu \\ |1,0\rangle &= \frac{1}{\sqrt2}(ud + du) \\ |1,-1\rangle &= dd \ \end{aligned} \] Lo stato antisimmetrico con \( I=0 \) corrisponde, invece, alla particella $ Λ $. \[ |0,0\rangle = \frac{1}{\sqrt2}(ud - du) \] 

Se l’isospin totale vale \( I = 1 \) allora il numero di stati possibili è:

\[ 2I + 1 = 2 \cdot 1 + 1 = 3 \]

Questo significa che il multipletto di isospin contiene tre stati distinti, caratterizzati dai valori della proiezione \( I_3 \):

Il multipletto di isospin contiene quindi tre stati:

$$ I_3 = \{ +1,\ 0,\ -1 \} $$

Nel caso delle particelle Σ, questi tre stati corrispondono rispettivamente alle particelle

• $ \Sigma^+ $
• $ \Sigma^0 $
• $ \Sigma^- $

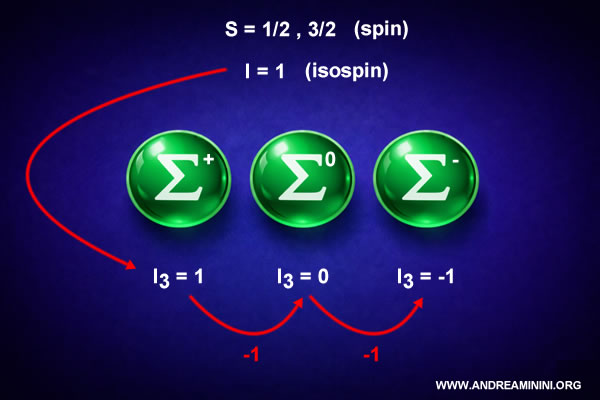
Spin delle particelle Sigma

Esistono due famiglie distinte di particelle Sigma, che si differenziano per il valore dello spin totale.

• Sigma (Σ)
  Le particelle Σ ordinarie hanno spin \( \frac{1}{2} \) e appartengono all’ottetto barionico. In questo caso gli spin dei quark non sono tutti allineati (es. una possibile configurazione è ↑↑↓) e per questa ragione hanno lo spin pari a 1/2. La somma degli spin è: $$ \tfrac 12 + \tfrac 12 - \tfrac 12= \tfrac 12$$ 
• Sigma stella (Σ*)
  Le particelle Σ* hanno spin \( \frac{3}{2} \) e appartengono al decupletto barionico. In questo caso i tre quark hanno gli spin tutti allineati (↑↑↑) e per questa ragione hanno lo spin 3/2.. La somma diventa: $$ \tfrac 12 + \tfrac 12 + \tfrac 12= \tfrac 32$$ perché i quark sono allineati. Quindi, sono stati eccitati delle particelle sigma. A. Sono stati eccitati delle Sigma. Le Sigma stella hanno i quark tutti allineati   

La differenza tra le due famiglie nasce dall’allineamento degli spin dei quark.

Questo spiega perché esistano più particelle con la stessa composizione in quark ma con masse e spin diversi.

E così via.