Elicità di una particella
Nella fisica delle particelle l'elicità $ h $ indica se lo spin di una particella è allineato oppure opposto alla direzione del suo moto.
- $ h = +1 $ se lo spin è parallelo alla direzione del moto. In questo caso la particella è detta "destrorsa".
- $ h = -1 $ se lo spin è antiparallelo (opposto) alla direzione del moto. In questo caso la particella è detta "sinistrorsa".
In fisica delle particelle, l'elicità ($ h $) è definita come la proiezione dello spin ($\vec{S}$) sulla direzione del momento lineare (la quantità di moto $\vec{p}$).
$$ h = \frac{\vec{S} \cdot \vec{p}}{|\vec{p}|}$$
L’elicità non descrive una rotazione reale nello spazio, misura l’orientamento dello spin rispetto alla direzione del moto (vettore velocità) della particella.
Del resto, lo spin è una proprietà quantistica intrinseca, non è interpretabile come una rotazione meccanica di un corpo nello spazio.
Nota. Per rendere la spiegazione più intuitiva, nei disegni e negli esempi divulgativi lo spin viene talvolta rappresentato come una rotazione in senso orario o antiorario lungo la direzione del moto. Quindi, si può immaginare come il movimento di una vite: mentre la vite avanza (moto traslatorio), ruota su se stessa (moto rotatorio). A seconda del verso della rotazione rispetto alla direzione del movimento, si parla di elicità destrorsa o sinistrorsa. Questa rappresentazione è solo un aiuto visivo per rendere più intuitiva la spiegazione.
L’elicità è relativa all’osservatore
Per le particelle dotate di massa, l’elicità dipende dall’osservatore.
Se un osservatore corre più velocemente della particella e la supera, la vede muoversi nel verso opposto. In termini intuitivi, la rappresentazione della rotazione lungo la direzione del moto passa da oraria ad antioraria o viceversa.
Dal punto di vista fisico, ciò accade perché si inverte il verso della quantità di moto della particella rispetto all’osservatore, mentre lo spin resta invariato. Di conseguenza cambia il segno dell’elicità.
Ad esempio, considero una particella dotata di massa che si muove verso sinistra, con lo spin orientato verso destra. Nel sistema di riferimento inerziale $ S$ la particella si muove verso sinistra. In questo sistema, il verso della quantità di moto è opposto a quello dello spin, quindi la particella ha elicità negativa (sinistrorsa).
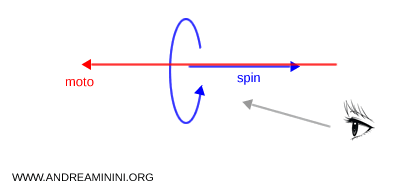
Considero ora un altro sistema di riferimento $ S' $, che si muove verso sinistra con una velocità maggiore di quella della particella. In questo sistema, la particella appare muoversi verso destra. Prima di superarla, un osservatore nel sistema $ S' $ la vede avvicinarsi, dopo averla superata la vede allontanarsi. Il verso della quantità di moto risulta quindi invertito rispetto a quello reale, mentre lo spin resta invariato perché è invariante in qualsiasi sistema di riferimento. Di conseguenza, nel sistema $ S' $ la particella ha elicità positiva (destrorsa).
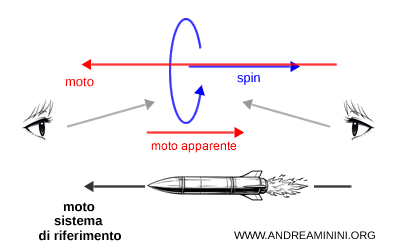
Questo esempio mostra che, per una particella dotata di massa, l’elicità dipende dal sistema di riferimento e non è una proprietà assoluta.
Fanno eccezione le particelle prive di massa, per le quali l’elicità è una proprietà assoluta e non dipende dal sistema di riferimento.
Una particella senza massa si muove sempre alla velocità della luce e non può essere superata da alcun osservatore. Di conseguenza, il verso della sua quantità di moto non può mai invertirsi.
Questo accade perché la velocità della luce è la velocità massima raggiungibile nell’Universo. Quindi, nessuna particella può muoversi più velocemente.
Ad esempio, un fotone può essere sinistrorso oppure destrorso, con pari probabilità. Un fotone sinistrorso non diventa destrorso cambiando sistema di riferimento, resta sinistrorso in tutti i sistemi di riferimento. Lo stesso vale per un fotone destrorso.
Il caso dei neutrini
Nel modello ideale i neutrini sono considerati particelle privi di massa. Quindi, per i neutrini ideali l’elicità non dipende dal sistema di riferimento dell’osservatore.
Inizialmente si pensava che i neutrini si comportassero come i fotoni, ossia che esistessero in egual misura neutrini destrorsi e sinistrorsi, con la stessa probabilità.
Il problema fu che gli esperimenti non confermarono questa ipotesi. I risultati sperimentali mostrarono una situazione completamente diversa.
In particolare, si osservò che:
- tutti i neutrini osservati sono sinistrorsi
- tutti gli antineutrini osservati sono destrorsi
Questo risultato rappresentò uno dei segnali più evidenti della violazione della parità nell’interazione debole.
In altre parole, mentre nelle altre interazioni fondamentali (forte, elettromagnetica e gravitazionale) la parità è conservata, cioè le leggi fisiche restano invariate sotto un’inversione spaziale, nell’interazione debole la parità non è conservata.
Nota. Oggi sappiamo che i neutrini non sono privi di massa, possiedono una massa seppure piccolissima. Di conseguenza, la loro velocità non è esattamente uguale alla velocità della luce e, in linea di principio, possono essere superati da un osservatore. In questo caso l’elicità non è più una quantità strettamente invariabile. Tuttavia, i neutrini prodotti nelle interazioni deboli sono quasi esclusivamente sinistrorsi, poiché l’interazione debole seleziona solo stati chirali sinistrorsi. La probabilità di osservare neutrini destrorsi è estremamente piccola e legata esclusivamente a effetti relativistici dovuti alla loro massa molto ridotta.
Come si misura l’elicità dei neutrini?
La misura diretta dell’elicità dei neutrini è estremamente difficile, perché i neutrini interagiscono molto debolmente con la materia. Di conseguenza, misurare direttamente il loro spin è praticamente impossibile.
Per questa ragione si ricorre a una tecnica di misura indiretta dell’elicità, basata sul decadimento del pione carico.
Nel decadimento di un pione negativo si producono un muone e un antineutrino:
\[ \pi^- \rightarrow \mu^- + \bar{\nu}_\mu \]
Se il decadimento avviene con il pione a riposo, il muone e l’antineutrino vengono emessi in direzioni opposte.
Nel sistema di riferimento del pione a riposo, se il muone ha quantità di moto \( \vec p \), l'antineutrino ha quantità di moto \( -\vec p \) perché si muovono in versi opposti.
Sapendo che il pione ha spin zero $ S=0 $, poiché lo spin totale iniziale è nullo, anche dopo il decadimento la somma degli spin delle particelle prodotte deve essere zero.
\[ S = \vec S_\mu + \vec S_{\bar\nu} = 0 \]
Di conseguenza, lo spin del muone e quello dell’antineutrino devono essere opposti.
\[ \vec S_{\bar\nu} = - \vec S_\mu \]
Per il muone l'elicità è proporzionale a:
\[ h_\mu \propto \vec S_\mu \cdot \vec p \]
Per l’antineutrino l'elicità è proporzionale a:
\[ h_{\bar\nu} \propto \vec S_{\bar\nu} \cdot (-\vec p) \]
Sostituendo \( \vec S_{\bar\nu} = - \vec S_\mu \) ottengo:
\[ h_{\bar\nu} \propto (-\vec S_\mu) \cdot (-\vec p) \]
I due segni meno si annullano:
\[ h_{\bar\nu} \propto \vec S_\mu \cdot \vec p \]
Pertanto, il prodotto scalare che definisce l’elicità è lo stesso per entrambe le particelle.
\[ h_\mu , h_{\bar\nu} \propto \vec S_\mu \cdot \vec p \]
In altre parole, se due particelle hanno spin opposti ma si muovono in versi opposti, la loro elicità è uguale.

Nota. Per spiegare questo concetto, spesso si usa la rappresentazione di una rotazione. Guardare la rotazione nella direzione del moto significa osservarla dalla punta della freccia del vettore velocità, cioè dal davanti, come se la particella ci venisse incontro. In questo punto di vista si fissa la convenzione secondo cui una rotazione in senso orario corrisponde a un’elicità destrorsa (come se si guardasse il quadrante di un orologio), mentre una rotazione in senso antiorario corrisponde a un’elicità sinistrorsa. Nel decadimento del pione, il muone e l’antineutrino si allontanano in direzioni opposte. Tuttavia, l’elicità di ciascuna particella si definisce guardando lungo la propria direzione di moto. In questo senso, sia il muone sia l’antineutrino risultano destrorsi.
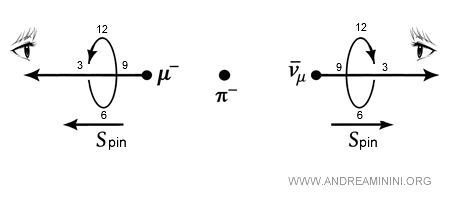
Dalle misure sperimentali emerge che il muone è destrorso, e quindi si deduce che anche l’antineutrino è destrorso.
Da questo risultato segue che, se gli antineutrini sono destrorsi, allora i neutrini sono sinistrorsi.
In questo modo si ottiene indirettamente l’elicità dei neutrini.
Confronto con il decadimento del pione neutro
Per capire perché il risultato ottenuto nel decadimento del pione carico è così significativo, è utile confrontarlo con il decadimento del pione neutro.
Il pione neutro decade generando due fotoni secondo il processo:
\[ \pi^0 \rightarrow \gamma + \gamma \]
Anche in questo caso il pione ha spin zero e, se il decadimento avviene a riposo, i due fotoni vengono emessi in direzioni opposte. Per conservare lo spin totale, i due fotoni devono avere elicità uguale.
Tuttavia, questo decadimento è governato dall’interazione elettromagnetica, che conserva la parità. Di conseguenza, non esiste alcuna preferenza tra elicità destrorsa e sinistrorsa. In media si osservano tante coppie di fotoni destrorsi quante coppie di fotoni sinistrorsi.
Il caso del pione carico è profondamente diverso. Il suo decadimento è mediato dall’interazione debole, che viola la parità. Per questo motivo, l’elicità delle particelle prodotte non è distribuita simmetricamente: l’antineutrino risulta sempre destrorso e, di conseguenza, il neutrino risulta sempre sinistrorso.
Il confronto mostra chiaramente che la selezione dell’elicità nei neutrini non è un effetto cinematico, né una conseguenza della conservazione dello spin, ma una proprietà fondamentale dell’interazione debole, che distingue in modo netto tra destra e sinistra.
In conclusione, l'interazione debole viola la parità mentre l'interazione forte la conserva. Questo è uno dei segnali più evidenti che le leggi della fisica, a livello fondamentale, non sono sempre invarianti sotto inversione spaziale.
La differenza tra elicità e chiralità
È importante distinguere tra elicità e chiralità, due concetti spesso confusi ma fisicamente diversi.
- L’elicità dipende dall’orientamento dello spin rispetto alla direzione di moto e, per le particelle dotate di massa, dipende dal sistema di riferimento dell’osservatore.
- La chiralità, invece, è una proprietà intrinseca delle particelle, legata alla struttura matematica delle interazioni fondamentali, e non dipende dall’osservatore.
Quindi, l’elicità è una grandezza che dipende dall’osservatore, mentre la chiralità è una proprietà intrinseca della particella fissata dalle interazioni fondamentali e non dipende dal sistema di riferimento.
Ad esempio, nell’interazione debole la natura seleziona solo particelle sinistrorse e antiparticelle destrorse in senso chirale. Per le particelle prive di massa, elicità e chiralità coincidono, poiché esse si muovono alla velocità della luce e non possono essere superate. È per questo motivo che, nel modello ideale, i neutrini risultano sempre sinistrorsi. In generale, per le particelle reali dotate di una massa molto piccola, elicità e chiralità non coincidono esattamente. Tuttavia, nella maggior parte dei processi fisici la differenza è trascurabile.
E così via.
