Relatività ristretta

La relatività ristretta (o speciale) è una teoria fisica formulata da Albert Einstein nel 1905. Estende la meccanica classica ai casi in cui gli oggetti si muovono a velocità comparabili con quella della luce nel vuoto.

In altre parole, la relatività ristretta modifica la nostra visione intuitiva di spazio e tempo, che nella meccanica classica erano assoluti.

Introduce una geometria spazio-temporale unificata e simmetrica, nella quale tempo e spazio sono entità relative che dipendono dallo stato di moto dell’osservatore.

I due postulati fondamentali

La teoria si fonda su due assiomi sperimentalmente verificati:

• Principio di relatività
  Le leggi della fisica sono identiche in tutti i sistemi di riferimento inerziali, cioè quelli non accelerati. Quindi, non esiste un sistema di riferimento assoluto: le equazioni della fisica devono valere allo stesso modo per ogni osservatore in moto rettilineo uniforme.
• Costanza della velocità della luce
  La velocità della luce nel vuoto ha lo stesso valore per tutti gli osservatori, indipendentemente dal moto della sorgente o dell’osservatore. Questa velocità è una costante universale: $$ c \approx 3 \times 10^8 \,\text{m/s} $$

I due postulati portano a modifiche profonde del concetto di spazio e tempo, che nella meccanica classica erano considerati assoluti.

In particolar modo introduce il concetto della dilatazione del tempo, la contrazione delle lunghezze, la relatività della simultaneità e l'equivalenza tra massa ed energia .

Nota. Nel 1915, Einstein estenderà la relatività anche ai sistemi accelerati e alla gravità, formulando la Relatività Generale, in cui lo spazio-tempo viene curvato dalla massa-energia. Quindi, la relatività ristretta o speciale (1905) non va confusa con la relatività generale (1915). Sono entrambe teorie di Einstein ma trattano aspetti diversi.

La dilatazione del tempo

La dilatazione temporale è il fenomeno per cui il tempo misurato da un osservatore esterno risulta più lungo rispetto al tempo misurato nel sistema in cui l’evento ha luogo (cioè il sistema a riposo rispetto al fenomeno).

E' uno degli effetti più sorprendenti della relatività ristretta, il tempo non scorre allo stesso modo per tutti gli osservatori.

Un orologio in movimento risulta più lento rispetto al tempo di un osservatore esterno .

$$ \Delta t = \gamma \cdot \Delta t_0 \quad \text{con} \quad  \gamma = \frac{1}{\sqrt{1 - \frac{v^2}{c^2}}} $$

Dove:

• $\Delta t_0 $ è il tempo proprio, cioè il tempo misurato nel sistema in movimento in cui si trova l’orologio.
  Questo tempo è solidale al fenomeno e si dice che è misurato a riposo rispetto all’evento osservato.
• $ \Delta t $ è il tempo dilatato, misurato da un osservatore esterno in moto relativo rispetto all’orologio: per lui, l’orologio in movimento scorre più lentamente rispetto agli orologi nel proprio sistema.
• $\gamma $ è il fattore di Lorentz che è sempre maggiore di 1 se $v>0 $.

Al crescere della velocità relativa verso la velocità della luce, la dilatazione temporale aumenta, e il tempo scorre sempre più lentamente nel sistema in movimento rispetto al riferimento dell’osservatore esterno.

Ad esempio, se $t$ è il tempo misurato sulla Terra e osserviamo un’astronave passare a velocità prossima a quella della luce, allora il tempo $ t' $ a bordo dell’astronave scorre molto più lentamente rispetto al tempo terrestre.

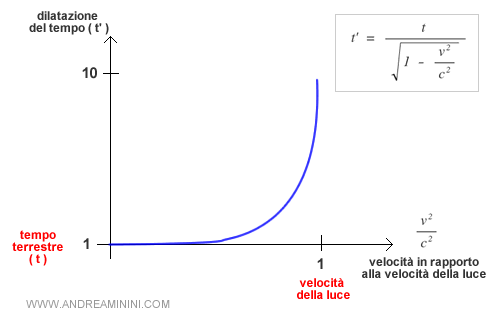
Questo è alla base del famoso esempio del paradosso dei gemelli.

Due gemelli si trovano sullo stesso sistema di riferimento (la Terra). Uno resta a Terra, l’altro viaggia nello spazio in un'astronave a velocità relativistica prossima alla luce. Al suo ritorno, i due si ritrovano, ma non hanno più la stessa età:

• Il gemello rimasto sulla Terra ha vissuto un tempo più lungo. E' invecchiato.
• Il gemello viaggiatore è ancora giovane.

Questo effetto si spiega con la dilatazione temporale: durante il viaggio, il tempo a bordo dell’astronave è trascorso più lentamente rispetto al tempo misurato sulla Terra.

Va detto che la dilatazione del tempo non è solo un effetto teorico: è confermata sperimentalmente, in modo chiaro e ripetuto, soprattutto nella fisica delle particelle ad alte energie.

Ad esempio, una particella instabile (come un muone) si muove a velocità relativistica. Se il suo tempo di decadimento a riposo è \$ \Delta t_0 = 2.2 ,\mu s\$, per un osservatore terrestre che la vede viaggiare a $v = 0.99 \cdot c $, cioé quasi alla velocità della luce, il tempo osservato sarà $ \Delta t = 15.6 ,\mu s $ $$ \gamma \approx \frac{1}{\sqrt{1 - 0.99^2}} \approx 7.1 $$ $$ \Delta t = 7.1 \cdot 2.2 \approx 15.6 \,\mu s $$ Quindi, il muone vive più a lungo del previsto perché il tempo per lui “scorre più lentamente”.

La contrazione delle lunghezze

La contrazione delle lunghezze è il fenomeno per cui un oggetto in movimento appare accorciato lungo la direzione del moto rispetto alla sua lunghezza misurata nel proprio sist

Un oggetto in movimento appare accorciato lungo la direzione del moto rispetto alla sua lunghezza a riposo.

$$ L = \frac{L_0}{\gamma} $$

Dove:

• $L_0 $ è la lunghezza propria nel sistema in cui l’oggetto è fermo.
• $L $ è la lunghezza misurata da un osservatore in cui l’oggetto si muove.

Ad esempio, un'astronave lunga 100 m a riposo si muove a $v = 0.8 \cdot c $ rispetto alla Terra, circa al 80% della velocità della luce. In questo caso il fattore di Lorentz è 1.667. $$ \gamma = \frac{1}{\sqrt{1 - 0.8^2}} = \frac{1}{\sqrt{0.36}} = \frac{1}{0.6} \approx 1.667 $$ La lunghezza dell'astronave in movimento, vista dall'esterno, è di circa 60 metri. $$ L = \frac{100}{1.667} \approx 60 \,\text{m} $$ Quindi, l’astronave appare più corta per l’osservatore terrestre.

La relatività della simultaneità

Due eventi simultanei in un sistema di riferimento non sono simultanei in un altro in moto rispetto al primo.

La simultaneità, quindi, non è assoluta, ma dipende dal sistema dell’osservatore.

Questo effetto emerge dalle trasformazioni di Lorentz, che mostrano come tempo e spazio siano collegati in modo non separabile.

Ad esempio, un osservatore a bordo di un treno in moto vede due lampi colpire contemporaneamente le estremità del vagone. Un osservatore fermo a terra non li vedrà come simultanei, perché la luce percorre distanze diverse a causa del moto del treno.

L'equivalenza massa-energia

La massa e l’energia sono due aspetti della stessa grandezza fisica.

Questa equivalenza è la nota legge di Einstein:

$$ E = mc^2 $$

Dove:

• $E $ è l’energia contenuta nella massa a riposo $m $.
• $c $ è la velocità della luce nel vuoto.

Questa relazione è alla base del funzionamento delle centrali nucleari e delle bombe atomiche.

Ad esempio, un grammo di massa (0.001 kg) equivale a: $$ E = 0.001 \cdot (3 \times 10^8)^2 = 9 \times 10^{13} \,\text{J} $$ Un’energia enorme, equivalente all’esplosione di decine di tonnellate di TNT.

E così via.