Eightfold Way
La Eightfold Way (tradotto "Via Ottoposta") è uno schema di classificazione delle particelle subatomiche che raggruppa i barioni e mesoni in famiglie con proprietà simili, usando due parametri principali (numeri quantici):
- La carica elettrica $Q$
- La stranezza $S$ ossia il numero quantico che misura la presenza di quark o antiquark "strange" nella particella.
E' stato ideato da Murray Gell-Mann nel 1961 e, indipendentemente, anche da Yuval Ne’eman, basato sulla simmetria matematica SU(3).
Questo schema ha come obiettivo mettere ordine nel caos della particelle degli anni ’50-’60 (la cosiddetta "particle zoo era"), quando erano state scoperte decine di nuove particelle ma mancava un sistema coerente per catalogarle.
Per rappresentare la classificazione vengono usate anche delle figure geometriche regolari (esagono, triangolo, ecc.).
Esempio
Ad esempio, per classificare i barioni la stranezza $ S $ viene misurata su assi orizzontali mentre la carica $ Q $ su assi diagonali.
Questo gruppo è conosciuto come ottetto dei barioni.
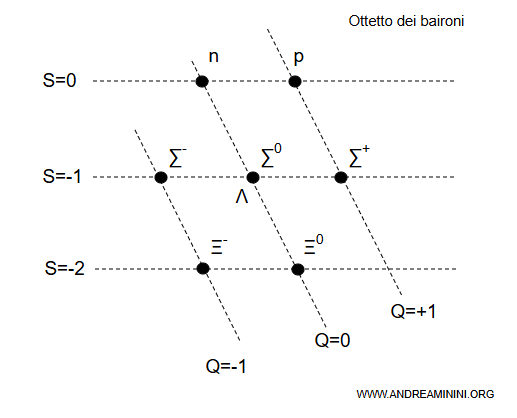
Si chiama "ottetto" perchè in questa figura esagonale sono classificate 8 particelle (baironi).
Nota. In questo schema sono classificati dei barioni (particelle con spin $ \frac{1}{2} $ composte da tre quark), ordinati in funzione della stranezza ($S$, sull’asse verticale) e della carica elettrica ($Q$, sull’asse orizzontale).
- In alto, con $S = 0$, si trovano il neutrone $n$ con carica nulla ($Q = 0$) e il protone $p$ con carica positiva ($Q = +1$).
- Al livello $S = -1$ compaiono le tre particelle $\Sigma $ ( $\Sigma^{+}$, $\Sigma^{0}$, $\Sigma^{-}$) e la particella $\Lambda$ ($Q = 0$).
- In basso, con $S = -2$, sono rappresentate le particelle $\Xi$, entrambe contenenti due quark strange $ s $. La prima $ \Xi^{-} = (d s s) $ ha carica negativa ($Q = -1$), mentre la seconda $ \Xi^{0} = (u s s) $ ha carica nulla ($Q = 0$).
Uno schema simile, sempre esagonale, è stato usato per classificare i mesoni.
Ecco come si presenta l'ottetto dei mesoni.
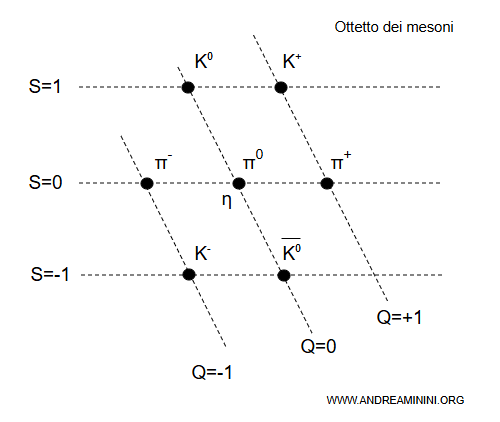
In questo caso il primo asse orizzontale in alto misura la stranezza $ S=1 $ e l'ultimo in basso $ S=-1 $ al contrario del precedente.
Nota. Questo diagramma mostra mesoni pseudoscalari, particelle composte da un quark e un antiquark, ordinati in funzione della stranezza ($S$, asse verticale) e della carica elettrica ($Q$, asse orizzontale).
- In alto, con $S = +1$, si trovano il kaone neutro $K^{0}$ ($Q = 0$) e il kaone carico positivo $K^{+}$ ($Q = +1$).
- Al livello $S = 0$ compaiono i tre pioni ($\pi^{-}$, $\pi^{0}$, $\pi^{+}$) e la particella $\eta$.
- In basso, con $S = -1$, sono rappresentati il kaone carico negativo $K^{-}$ ($Q = -1$) e l'antikaone neutro $\overline{K}^{0}$ ($Q = 0$). La disposizione riflette la simmetria di sapore $SU(3)$, che raggruppa questi mesoni in un ottetto in base ai loro numeri quantici.
Queste disposizioni sono state utili perché hanno tentato di dare una prima classificazione alle particelle strange (strane) tenendo conto anche della "stranezza", il nuovo numero quantito introdotto negli anni '50.
Consentirono anche di predirre l'esistenza di alcune particelle sconosciute. Ad esempio, della particella $ \Omega^- $ (carica - 1, stranezza - 3), scoperta nel 1964.
D'altra parte ha anche dei limiti.
Nota. Ad esempio, la simmetria è solo approssimata e le masse non sono uguali all’interno dello stesso multiplet. Non spiega perché le particelle abbiano certe masse o interagiscano in un certo modo.
Fu comunque il primo tentativo di classificazione e preparò il terreno per il modello a quark, in cui le particelle dell’ottetto e del decupletto vengono spiegate come combinazioni di tre quark (u, d, s).
Il decupletto barionico
Dopo l’identificazione dell’ottetto dei barioni con spin \( \tfrac12 \), le osservazioni sperimentali rivelarono l’esistenza di altre particelle con proprietà simili ma con spin diverso, in particolare con spin \( \tfrac32 \).
Questi nuovi stati non potevano essere collocati nell’ottetto già noto, ma la loro distribuzione mostrava regolarità troppo nette per essere considerate casuali. Questo suggeriva che la simmetria SU(3) fosse più ricca di quanto apparisse inizialmente.
Dal punto di vista matematico, combinando tre quark nella rappresentazione fondamentale di SU(3) si ottiene la decomposizione
$$ 3 \otimes 3 \otimes 3 = 10 \oplus 8 \oplus 8 \oplus 1 $$
Dove $ 10 $ è il decupletto, $ 8 $ è l'ottetto e $ 1 $ è un singoletto.
In altre parole, se esiste l'ottetto allora deve esistere anche il decupletto, perché entrambi emergono naturalmente dalla stessa struttura matematica della simmetria SU(3).
Il decupletto barionico corrisponde a configurazioni completamente simmetriche nello spazio dei sapori e, proprio per questa simmetria massima, è associato a barioni con spin totale \( \tfrac32 \).
A differenza dell’ottetto, che ha una forma esagonale con una particella centrale, il decupletto ha una struttura a triangolo equilatero, composta da dieci stati distribuiti su quattro livelli.

Nota. La forma triangolare non è un semplice disegno: riflette una proprietà fisica importante. Nel decupletto gli spin dei quark sono allineati, quindi lo spin totale è \( \tfrac32 \) e la simmetria interna è massima.
Il diagramma del decupletto viene costruito disponendo le particelle in base a due numeri quantici: la stranezza \( S \) e la carica elettrica \( Q \). Scendendo dall’alto verso il basso, la stranezza diminuisce e aumenta il numero di quark strange presenti.
Al vertice superiore del triangolo si trovano quattro particelle \( \Delta \) prive di quark strange, composte solo da quark up \( u \) e down \( d \).
- \( \Delta^{++} = uuu \)
- \( \Delta^{+} = uud \)
- \( \Delta^{0} = udd \)
- \( \Delta^{-} = ddd \)
Subito sotto compaiono tre particelle \( \Sigma \) con un quark strange \( s \) e due quark leggeri. La presenza dello strange rompe leggermente la simmetria e aumenta la massa rispetto alle particelle \( \Delta \).
- \( \Sigma^{*+} = uus \)
- \( \Sigma^{*0} = uds \)
- \( \Sigma^{*-} = dds \)
Nota. L’asterisco indica uno stato con spin \( \tfrac32 \). La differenza tra \( \Sigma \) e \( \Sigma^{*} \) non è la composizione in quark, che resta la stessa, ma il modo in cui gli spin si combinano. Quando gli spin sono allineati (↑↑↑) si ottiene \[ \tfrac12 + \tfrac12 + \tfrac12 = \tfrac32 \] mentre per combinazioni non completamente allineate (↑↑↓, ↑↓↑, ↓↑↑) si ottiene \[ \tfrac12 + \tfrac12 - \tfrac12 = \tfrac12 \] quindi lo stato appartiene all’ottetto. Lo stesso ragionamento vale per \( \Xi^{*} \).
Nel livello successivo compaiono due particelle \( \Xi \), composte da due quark strange e un quark leggero. La massa aumenta ulteriormente.
- \( \Xi^{*0} = uss \)
- \( \Xi^{*-} = dss \)
Alla base del triangolo si trova un’unica particella, la \( \Omega^{-} \), composta esclusivamente da quark strange:
$$ \Omega^{-} = sss $$
Questa particella rappresenta il punto estremo del decupletto ed è caratterizzata da stranezza \( S=-3 \), carica \( Q=-1 \) e spin \( \tfrac32 \).
La previsione della particella \( \Omega^{-} \). Il successo più celebre del modello fu la previsione della particella \( \Omega^{-} \). Questa particella occupa il vertice inferiore del decupletto e completa la struttura simmetrica prevista teoricamente, ma al momento della formulazione del modello non era ancora stata osservata. La sua scoperta sperimentale nel 1964 confermò in modo spettacolare la validità della simmetria SU(3) e la potenza predittiva del modello dei quark.
E così via.
