Fotone
Il fotone è la particella elementare che costituisce il quanto del campo elettromagnetico.
È il mediatore dell’interazione elettromagnetica nella teoria quantistica dei campi, così come il gluone lo è per l’interazione forte e i bosoni $ W $ e $ Z $ per quella debole.
Il fotone ha massa a riposo nulla e carica elettrica nulla. Ha spin 1, quindi è un bosone vettore.
Si muove sempre alla velocità della luce nel vuoto alla velocità della luce $ c=299 792 458 \ m/s $ ed è indistinguibile da altri fotoni della stessa energia.
Natura ondulatoria e corpuscolare
Il fotone mostra una doppia natura:
- Ondulatoria, nei fenomeni di interferenza, diffrazione, polarizzazione.
- Corpuscolare, nei fenomeni come l’effetto fotoelettrico, lo scattering Compton, la radiazione di corpo nero.
Questa dualità è alla base della meccanica quantistica e porta al principio di complementarità: il fotone non è “onda o particella”, ma entrambe le cose, e si comporta da onda o da particella a seconda del fenomeno osservato.
Energia e quantità di moto
L’energia di un fotone è direttamente proporzionale alla sua frequenza $\nu$, secondo la relazione:
$$ E = h \nu $$
Dove $h$ è la costante di Planck $ h \approx 6{,}626 \times 10^{-34} \ \text{J·s} $ e $\nu$ è la frequenza della radiazione associata.
La quantità di moto del fotone, pur non avendo massa, è data da:
$$ p = \frac{E}{c} = \frac{h\nu}{c} = \frac{h}{\lambda} $$
Dove $\lambda$ è la lunghezza d’onda.
La scoperta del fotone
Il fotone non fu scoperto con un singolo evento o esperimento, ma emerse gradualmente tra il 1900 e il 1924.
Planck e la radiazione quantizzata (1900)
Cercando di spiegare lo spettro del corpo nero, Max Planck introdusse l’idea che la radiazione elettromagnetica venga emessa in quantità discrete di energia, ovvero in pacchetti detti quanti:
$$ E = h\nu $$
Dove $ E $ è l'energia della radiazione elettromagnetica, $\nu$ è la frequenza della radiazione associata e $ h \approx 6{,}626 \times 10^{-34} \ \text{J·s} $ è la costante di Planck.
In altre parole, l’energia di un fotone è direttamente proporzionale alla sua frequenza $\nu$ e non può assumere valori continui, ma solo valori discreti multipli di $ hν $.
$$ E = n \cdot h\nu $$
Dove $ n=1,2,3,... $ è un numero intero che indica il numero di quanti.
Tuttavia, per Planck questa quantizzazione non rappresentava una proprietà fisica fondamentale del campo elettromagnetico, ma era soltanto un'ipotesi matematica introdotta per adattare la teoria ai dati sperimentali e risolvere la cosiddetta “catastrofe ultravioletta”.
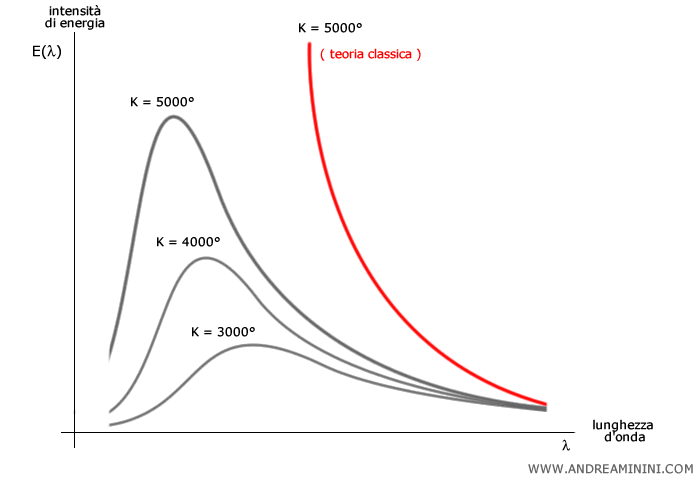
Cos'è la catastrofe ultravioletta? La catastrofe ultravioletta è un famoso paradosso della fisica classica che emerse alla fine dell’Ottocento, quando si cercava di spiegare la radiazione emessa da un corpo nero, cioè da un oggetto ideale che assorbe e riemette tutta la radiazione elettromagnetica che riceve. Secondo la teoria classica, basata sull’elettromagnetismo e sulla meccanica statistica (in particolare la legge di Rayleigh-Jeans), l’energia emessa da un corpo nero per ogni frequenza $\nu$ doveva aumentare con la frequenza secondo questa legge: $$ \rho(\nu, T) = \frac{8 \pi \nu^2}{c^3} kT $$ Dove
- $\rho(\nu, T)$ è la densità spettrale di energia (energia per unità di volume per frequenza)
- $\nu$ è la frequenza della radiazione
- $T$ è la temperatura del corpo
- $k$ è la costante di Boltzmann
- $c$ è la velocità della luce
Secondo questa formula a bassa frequenza, la previsione è corretta, ma a frequenze molto alte, cioè nell’ultravioletto e oltre, la densità di energia diverge all’infinito. Quindi la teoria classica prevedeva che un corpo nero avrebbe dovuto emettere un'energia infinita ad alte frequenze. Questo era assurdo, perché gli esperimenti mostravano un massimo nell’emissione (un “picco”) e poi un calo per alte frequenze. Inoltre, nessun corpo al mondo emette energia infinita! Questo disastro teorico fu chiamato "catastrofe ultravioletta".
La soluzione di Planck (1900)
Max Planck risolse il problema con un’ipotesi rivoluzionaria: l’energia della radiazione elettromagnetica non può variare in modo continuo, ma solo in quanti:
$$ E = h \nu $$
Dove $ E $ è l'energia della radiazione elettromagnetica, $\nu$ è la frequenza della radiazione e $ h \approx 6{,}626 \times 10^{-34} \ \text{J·s} $ è una costante matematica individuata da Planck per adeguarsi ai dati sperimentali. Secondo Planck l’energia scambiata non può essere qualsiasi, ma solo multipli interi di una quantità elementare:
$$ E = n h \nu \quad \text{con} \quad n = 1, 2, 3, \dots $$
Dove $n$ è un numero intero positivo. Questa quantità elementare di energia $h\nu$ è il quanto di energia. In altre parole, la radiazione non può essere emessa o assorbita in modo continuo, ma solo a "scatti", di quantità minime indivisibili (pacchetti di energia o quanti). ll quanto è quindi l’unità fondamentale di energia per la radiazione a una certa frequenza. Planck usò l’idea del quanto per costruire una nuova formula per la densità spettrale di energia (la legge di Planck):
$$ \rho(\nu, T) = \frac{8 \pi \nu^2}{c^3} \cdot \frac{h\nu}{e^{h\nu/(kT)} - 1} $$
Dove $h \nu$ è l’energia quantizzata del fotone. Questa formula si comporta come la legge classica per basse frequenze a basse frequenze ($h\nu \ll kT$) ma decade esponenzialmente per alte frequenze ($h\nu \gg kT$), ossia alle basse lunghezze d'onda, evitando il problema catastrofe ultravioletta. Questa fu la prima manifestazione della quantizzazione in fisica, e segnò la nascita della fisica quantistica. Va comunque detto che Planck non pretendeva di spiegare perché la radiazione elettromagnetica fosse quantizzata, ipotizzava solo che lo fosse.
Einstein e l’effetto fotoelettrico (1905)
Einstein partì da un fenomeno sperimentale ben noto: quando si illumina un metallo con una luce ultravioletta o con luce di frequenza abbastanza alta, si osserva che alcuni elettroni vengono espulsi dal metallo.
Questo fenomeno è conosciuto come effetto fotoelettrico.
Questi elettroni fotoemessi si muovono liberi nello spazio, come se la luce li avesse colpiti e "strappati via" dal metallo.
Nota. Fino ad allora si pensava che la luce, essendo un’onda elettromagnetica, trasferisse energia in modo continuo: più intensa era la luce, più energia avrebbe trasmesso agli elettroni. Ma questo non spiegava i risultati sperimentali. In particolare:
- Sotto una certa frequenza (cioè luce troppo “rossa”), non venivano espulsi elettroni, nemmeno aumentando l’intensità della luce.
- Aumentando la frequenza della luce (cioè usando luce più “blu” o "viola"), gli elettroni uscivano con più energia, anche se la luce era debole.
Nel 1905 Einstein propose una spiegazione nuova e audace: la luce non si comporta solo come un’onda, è composta da quanti di energia, piccoli pacchetti di energia che oggi chiamiamo "fotoni", e ogni fotone trasporta un’energia pari a
$$ E = h \nu $$
Dove $h$ è la costante di Planck e $\nu$ è la frequenza della luce.
Quando un fotone colpisce un elettrone in un metallo gli trasferisce tutta la sua energia ( $ h \nu $) che l'elettrone utilizza per liberarsi dal metallo, vincendo una barriera chiamata "funzione lavoro" ($w$).
L’energia rimanente diventa energia cinetica dell'elettrone in uscita:
$$ E_{\text{cinetica}} \leq h\nu - w $$
Einstein spiegò che, se la frequenza della luce è troppo bassa, nessun elettrone esce, qualunque fosse l’intensità della radiazione elettromagnetica.
$$ w > h\nu $$
Quando la frequenza $ \nu $ supera una certa soglia ($ w $), invece, gli elettroni iniziano a uscire.
$$ w \leq h\nu $$
Più alta è la frequenza, più energia hanno gli elettroni espulsi.
Aumentando l'intensità della luce vengono espulsi più elettroni, ma non con più energia.
Ad esempio, la prima radiazione $ \nu_1 $ (rossa) ha una frequenza troppo bassa e nessun elettrone si stacca dalla barra di metallo, la seconda radiazione $ \nu_2 $ (verde) ha una frequenza sufficiente e alcuni elettroni si staccano dal metallo con energia cinetica $ E_2$. La terza radiazione $ \nu_3 $ (viola) ha una frequenza ancora più alta e gli elettroni si staccano con un'energia cinetica maggiore $ E_3 > E_2 $
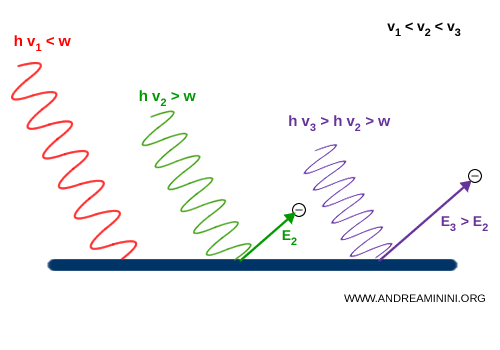
Quindi, Einstein comprese che l'energia degli elettroni fotoemessi dipendeva dalla frequenza, non dall’intensità della luce (radiazione elettromagnetica).
Questa idea, semplice ma rivoluzionaria, trasformò per sempre la fisica.
Nota. L’idea di Einstein fu inizialmente mal vista, poiché evocava la vecchia teoria corpuscolare di Newton ormai screditata. Persino Millikan, pur confermando sperimentalmente la formula, non l’accettava concettualmente. Ci vollero circa venti anni e diverse conferme sperimentali prima che la comunità scientifica la accettasse.
L'esperimento di Compton (1923)
In un esperimento Compton confermò che la luce ha comportamento particellare, con variazione della lunghezza d’onda:
$$ \lambda' = \lambda + \lambda_c(1 - \cos\theta) $$
Dove $ \lambda_c $ è la lunghezza d'onda di Compton.
Si trattava di un urto elastico relativistico, conferma definitiva del fotone come portatore di quantità di moto ed energia.
Nota. Fu però Gilbert Lewis nel 1926 a proporre il nome "fotone" per indicare questi quanti di luce
Fotone e teoria quantistica dei campi (QFT)
La teoria quantistica dei campi (QFT) ha sostituito la concezione classica del "campo continuo" con una descrizione più "granulare".
In questo quadro, il campo elettromagnetico è considerato quantizzato, cioè composto da “quanti” discreti: i fotoni.
Le interazioni non sono più viste come forze diffuse nello spazio, ma come scambi di particelle mediatrici tra le cariche.
Queste particelle mediatrici, come i fotoni, agiscono da messaggeri quantistici, capaci di produrre attrazione o repulsione a seconda delle caratteristiche dell’interazione.
Ad esempio, la repulsione tra due elettroni viene reinterpretata come uno scambio continuo di fotoni virtuali, che trasmettono l’interazione tra le particelle.
In conclusione, il fotone è nato da un’ipotesi matematica di Planck, è stato radicalmente reinterpretato da Einstein, e solo con Compton ha ricevuto una legittimazione sperimentale definitiva.
La sua natura duale (onda/particella) è pienamente compresa solo nella teoria quantistica dei campi, dove funge da "quanto del campo elettromagnetico" e mediatore delle interazioni elettromagnetiche.
Il fotone nella fisica quantistica
Nella fisica classica due cariche (come due elettroni) si respingono perché ognuna genera un campo elettrico che agisce sull’altra.
Nella fisica quantistica, invece, in un campo continuo c'è uno scambio continuo di fotoni, come se le cariche si lanciassero delle "particelle di forza" che comunicano il messaggio di avvicinarsi o allontanarsi.
Attenzione. Non è come lanciarsi oggetti. Un errore comune è immaginare che le particelle mediatrici, come il fotone, agiscano come oggetti che rimbalzano, tipo due persone che si respingono lanciandosi una palla. Ma non è così semplice, perché le particelle mediatrici possono causare sia attrazione che repulsione e non solo repulsione.
Ad esempio, in un atomo gli elettroni sono legati al nucleo perché vengono attratti elettricamente dai protoni, che hanno carica opposta.
In termini quantistici, questa attrazione si interpreta come un continuo scambio di fotoni virtuali tra elettroni e protoni, che mediano l’interazione elettromagnetica.
Allo stesso modo, due elettroni si respingono perché hanno la stessa carica, e anche questa repulsione può essere vista come il risultato dello scambio di fotoni virtuali tra le due particelle.

Questo vale anche per le altre forze, non solo per l’elettricità
Tutte le forze fondamentali (elettrica, debole, forte, gravitazionale) vengono spiegate, in teoria, come scambi di particelle mediatrici.
- Forza elettrica: due elettroni si respingono scambiandosi fotoni virtuali, le particelle mediatrici dell’interazione elettromagnetica.
- Forza debole: nel decadimento beta, un neutrone si trasforma in un protone emettendo un bosone W-.
, che poi decade in un elettrone e un antineutrino. - Forza forte: i quark all’interno dei protoni e neutroni restano uniti scambiandosi gluoni, che agiscono come “colla” nucleare.
- Gravità: in teoria due masse si attraggono perché scambiano gravitoni, particelle ipotetiche mai osservate sperimentalmente.
Nota. In molti casi, la fisica classica fornisce un’ottima approssimazione del comportamento dei campi, come avviene ad esempio per il campo elettromagnetico descritto dalla legge di Coulomb. Questo è possibile perché, in contesti come gli atomi stabili, lo scambio di numerosissimi fotoni virtuali rende il campo effettivamente continuo, e gli effetti della quantizzazione risultano trascurabili.Tuttavia, questa descrizione classica non è più sufficiente in fenomeni come l’effetto fotoelettrico (in cui la luce libera elettroni da un metallo) o lo scattering Compton (in cui un fotone urta un elettrone): in questi casi, il comportamento quantistico emerge chiaramente. La natura discreta del campo non può più essere ignorata, e i fotoni devono essere trattati come particelle vere e proprie, cioè come quanti di energia che non possono essere spiegati da un campo continuo.
E così via.
