Poligoni circoscritti a una circonferenza
Un poligono è detto poligono circoscritto a una circonferenza quando tutti i suoi lati sono tangenti alla stessa circonferenza.
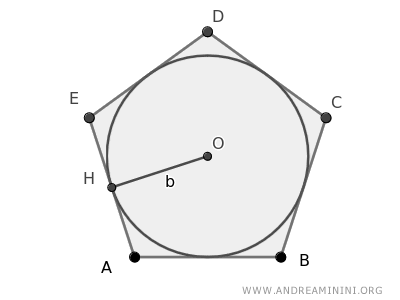
Quando un poligono è circoscritto a una circonferenza, si può dire anche che la circonferenza è inscritta nel poligono.
Il centro della circonferenza inscritta nel poligono è detto incentro mentre il raggio è detto inraggio.
La superficie della circonferenza è conosciuta come incerchio.
Non tutti i poligoni possono essere circoscritti a una circonferenza. Ad esempio, ogni triangolo può essere circoscritto in una circonferenza. Solo i quadrilateri in cui la somma delle lunghezze di due lati opposti è uguale all'altra coppia sono circoscritti. Tutti i poligoni regolari, come pentagoni e esagoni, sono circoscritti per definizione circoscritti a una circonferenza, in quanto la definizione stessa di un poligono regolare implica che il poligono sia circoscritto a una circonferenza.
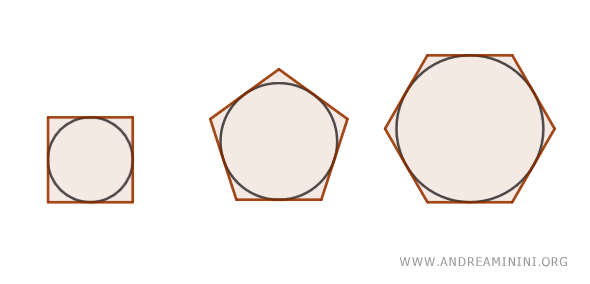
Area dei poligoni circoscritti
L'area di un poligono regolare circoscritto a una circonferenza è uguale al semiperimetro (p) per il raggio (r) della circonferenza $$ A = p \cdot r $$
Questa formula è dovuta al fatto che un poligono circoscritto è equivalente a un triangolo che ha per base il perimetro (P) del poligono e per altezza il raggio (r) della circonferenza.
Sapendo che l'area di un triangolo è il semiprodotto della base per l'altezza, ottengo la formula dell'area del poligono circoscritto.
$$ A = \frac{P \cdot r}{2} = \frac{P}{2} \cdot r = p \cdot r $$
Dove P è il perimetro mentre p è il semiperimetro. Quindi P=2p.
Poiché il raggio (r) della circonferenza coincide con l'apotema (a) del poligono regolare, l'area di un poligono regolare può essere calcolata anche moltiplicando il semiperimetro per l'apotema (a)
$$ A = p \cdot a $$
Esempio
Considero questo pentagono regolare circoscritto a una circonferenza di cui già conosco l'area A=15.48
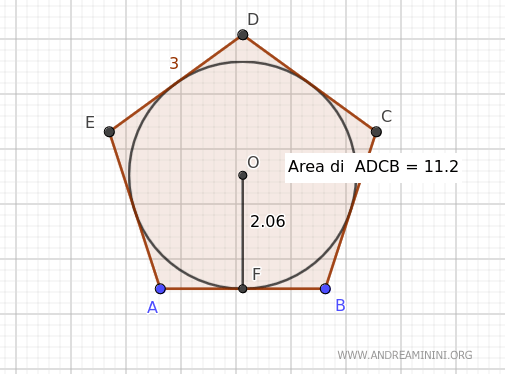
Di questo pentagono conosco anche la lunghezza di un lato = 3 e il raggio della circonferenza inscritta r=2.06
Il semiperimetro del pentagono è pari a 7.5
$$ p = \frac{3 \cdot 5}{2} = \frac{15}{2} = 7.5 $$
Se lo moltiplico per il raggio della circonferenza ottengo esattamente l'area del pentagono
$$ A = p \cdot r = 7.5 \cdot 2.06 ≅ 15.48 $$
Per dimostrarlo basta dividere la superficie del pentagono in cinque triangoli.
L'area di ogni triangolo si ottiene moltiplicando la base per l'altezza diviso due, ovvero il lato del pentagono per il raggio della circonferenza diviso due.
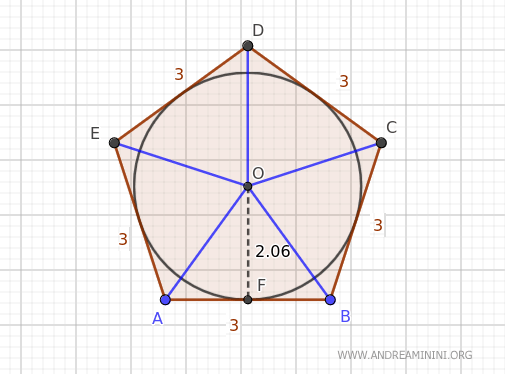
Sommando l'area di ogni triangolo ottengo l'area complessiva del pentagono.
$$ A = \frac{3 \cdot 2.06}{2} + \frac{3 \cdot 2.06}{2} + \frac{3 \cdot 2.06}{2} + \frac{3 \cdot 2.06}{2} + \frac{3 \cdot 2.06}{2} $$
$$ A = 5 \cdot \frac{3 \cdot 2.06}{2} $$
$$ A = \frac{5 \cdot 3}{2} \cdot 2.06 $$
Dove (5·3)/2 è il semiperimetro del pentagono mentre 2.06 è il raggio della circonferenza.
Il risultato finale è sempre lo stesso, l'area del pentagono regolare.
$$ A ≅ 15.48 $$
Lo stesso metodo di calcolo è applicabile a qualsiasi poligono regolare, perché ogni poligono regolare può essere circoscritto a una circonferenza.
Teorema dei poligoni circoscritti
Un poligono convesso è circoscritto a una circonferenza se e solo se tutte le bisettrici degli angoli si intersecano in uno stesso punto (incentro).
Se le bisettrici non passano tutte per uno stesso punto in comune, il poligono non è circoscrivibile a una circonferenza.
Vale anche il teorema inverso, se un poligono convesso è circoscritto a una circonferenza, allora tutte le bisettrici dei suoi angoli si incontrano in un unico punto comune, ovvero nel centro della circonferenza inscritta.
Tutti i triangoli e i poligoni regolari hanno un punto in cui si intersecano le loro bisettrici, chiamato incentro. Solo alcuni poligoni irregolari, quelli circoscritti a una circonferenza, hanno questa caratteristica.
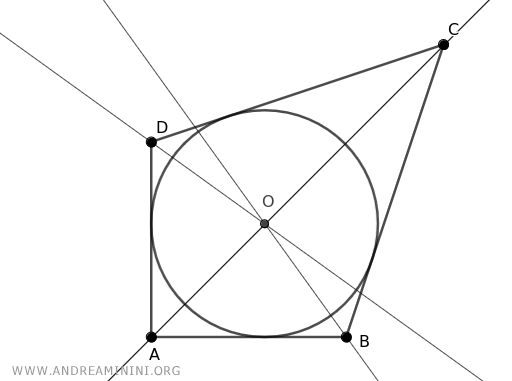
Un esempio pratico
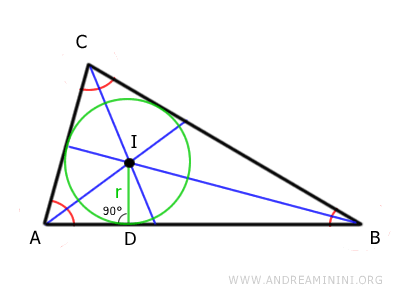
Ad esempio, le bisettrici di un triangolo passano sempre per uno stesso punto detto incentro del triangolo.
Se traccio una circonferenza centrata nell'incentro (I) con un opportuno raggio (r), la circonferenza è tangente a tutti i lati del triangolo.
La dimostrazione
Per dimostrare il teorema considero un poligono con le bisettrici degli angoli che si intersecano in un punto in comune O.
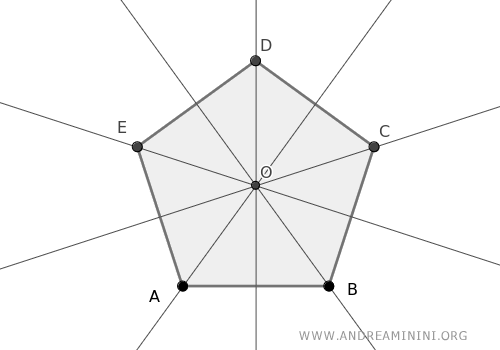
Dove per "bisettrice" dell'angolo intendo la retta che divide un angolo in due parti congruenti, ossia di pari ampiezza tra loro.
Devo dimostrare che il poligono può essere circoscritto a una circonferenza.
Per definizione la bisettrice è il luogo geometrico dei punti equidistanti dai lati.
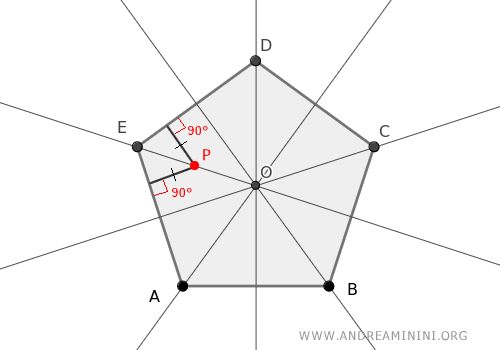
Quindi, il punto di intersezione delle bisettrici O ha la stessa distanza da tutti i lati del poligono.
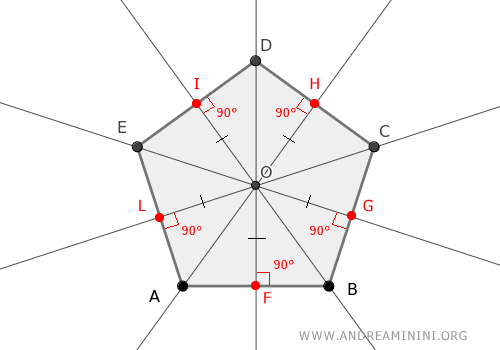
In altre parole, la distanza d tra il punto O e qualsiasi lato del poligono è la stessa.
$$ d = \overline{OF} = \overline{OG} = \overline{OH} = \overline{OI} = \overline{OL} $$
Questo vuol dire che nel punto O posso tracciare una circonferenza (incentro) con un raggio uguale alla distanza d che tocca tutti i lati del poligono.
Questa circonferenza è tangente a tutti i lati del poligono, quindi è una circonferenza inscritta nel poligono.
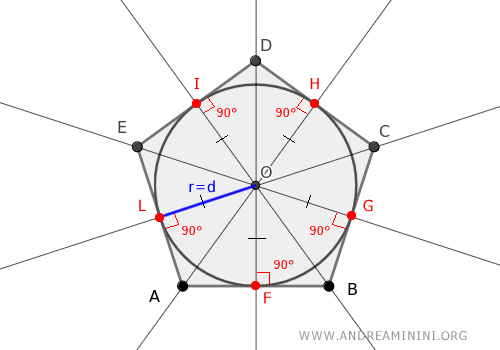
Questo dimostra che il poligono è circoscritto a una circonferenza.
E così via.
