Teorema della circonferenza per tre punti non allineati

In tre punti del piano non allineati passa una e una sola circonferenza.

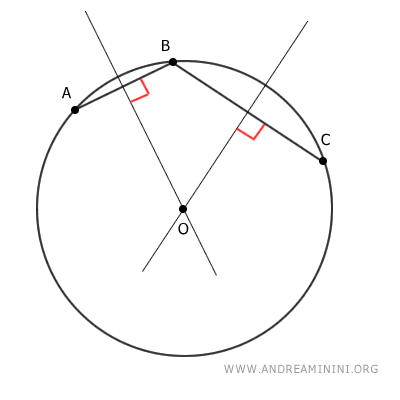
Questo teorema afferma sia l'esistenza che l'unicità di una circonferenza passante per tre punti non allineati.

Un esempio pratico

Traccio tre punti non allineati tra loro.

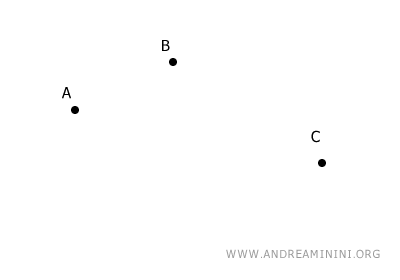
Congiungo due punti A e B con un segmento AB.

Poi, individuo il punto medio M del segmento AB e disegno l'asse del segmento, ossia la retta perpendicolare passante per il suo punto medio.

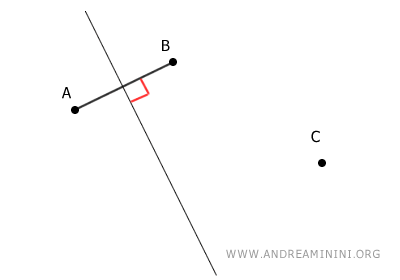
Ora congiungo altri due punti B e C con un segmento.

Poi, anche in questo caso, individuo il punto medio del segmento BC e traccio l'asse.

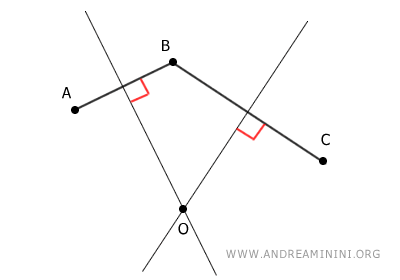
Gli assi dei segmenti AB e BC si intersecano nel punto O che ha la caratteristica d'essere equidistante da A, B e C.

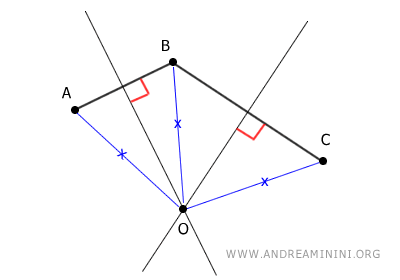
Spiegazione. Questo perché l'asse di un segmento rappresenta l'insieme di tutti i punti equidistanti dai due estremi del segmento. Nel punto O si intersecano sia l'asse di AB che l'asse di BC. Per questa ragione è equidistante da tutti e tre i punti.

A questo punto traccio una circonferenza con centro O e raggio OA (oppure OB o OC è lo stesso).

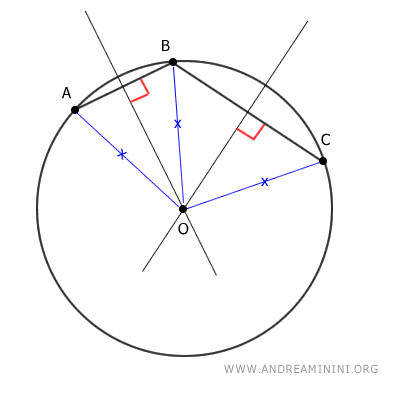
Il risultato finale è una circonferenza che passa per i tre punti A, B, C.

In questo modo ho ottenuto la circonferenza.

Non solo esistenza... ma anche unicità. Tuttavia, ciò che fa questo teorema non è solo trovare la circonferenza che passa per A, B e C, ma anche che non può esistere un'altra circonferenza diversa che faccia lo stesso. In breve i due assi possono intersecarsi solo in un solo punto. Quindi, non può esistere un altro punto diverso da O che sia equidistante da A, B e C. Lo spiego meglio nella dimostrazione.

La dimostrazione

Il teorema afferma l'esistenza e l'unicità di una circonferenza che passa per tre punti A, B, C non allineati nel piano.

Esistenza

Il punto O appartiene sia all'asse del segmento AB che all'asse del segmento BC.

Sapendo che l'asse di un segmento è un luogo geometrico con tutti i punti equidistanti da entrambi gli estremi del segmento.

Quindi, i segmenti OA e OB sono congruenti.

$$ \overline{OA} \cong \overline{OB} $$

Anche i segmenti OB e OC sono congruenti

$$ \overline{OB} \cong \overline{OC} $$

Per la proprietà transitiva, se OA=OB e OB=OC allora OA=OC

$$ \overline{OA} \cong \overline{OC} $$

Pertanto il punto O ha la stessa distanza da A, B e C.

Questo vuol dire che i punti A, B, C appartengono allo stesso luogo geometrico della circonferenza che ha per centro il punto O.

Unicità

I segmenti AB e BC non sono paralleli perché i tre punti A, B, C non sono allineati.

Quindi le rette passanti per AB e BC sono rette incidenti, ossia si intersecano in uno e un solo punto (B).

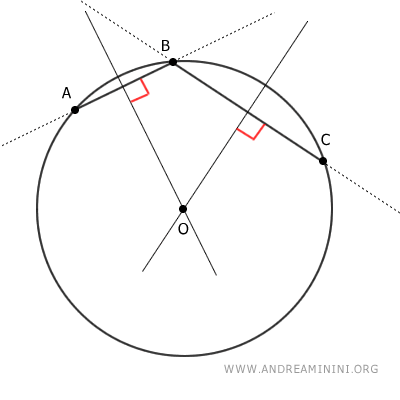
Sapendo che le perpendicolari di due rette incidenti sono a loro volta rette incidenti, deduco che anche gli assi dei segmenti AB e BC si intersecano in uno e un solo punto.

Pertanto, il punto O è l'unico punto equidistante dai tre i punti A, B, C. Non possono essercene altri.

Conclusione

In conclusione, esiste una e una sola circonferenza che passa per i tre punti A, B, e C.

E così via.