Poligoni inscritti in una circonferenza
Un poligono è detto poligono inscritto in una circonferenza quando tutti i suoi vertici giacciono sulla stessa circonferenza.
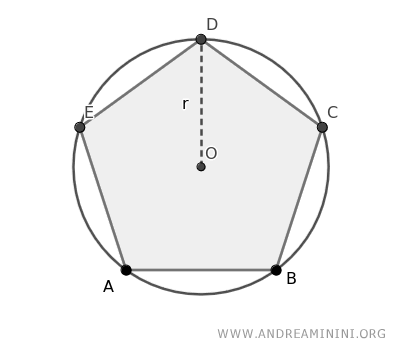
Quando un poligono è inscritto in una circonferenza, si può dire anche che la circonferenza circoscrive il poligono o la circonferenza è circoscritta al poligono. Il concetto è sempre lo stesso.
La lunghezza dei lati di un poligono inscritto può variare, ma tutti i vertici del poligono toccano la circonferenza.
Il centro della circonferenza circoscritta al poligono è chiamato circocentro.
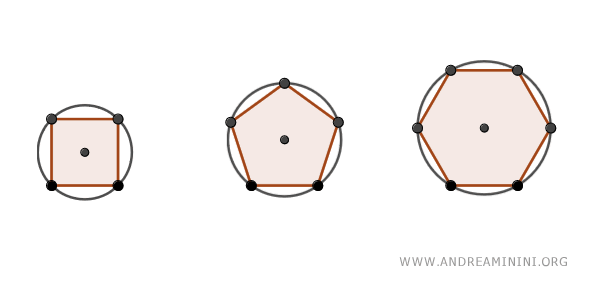
Non tutti i poligoni possono essere inscritti in una circonferenza. Ad esempio, il triangolo è sempre inscrivibile in una circonferenza, mentre solo alcuni quadrilateri possono essere inscritti. In generale, possono essere inscritti in una circonferenza tutti i poligoni regolari, come pentagoni, esagoni, ecc.,
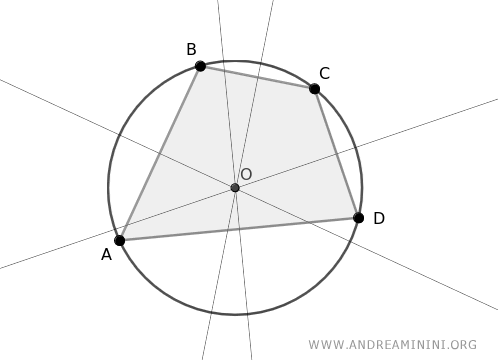
Un quadrilatero iscritto in una circonferenza ha sempre gli angoli opposti supplementari (α+β=180°).
Teorema dei poligoni inscritti
Un poligono può essere inscritto in una circonferenza se e solo se tutti gli assi (perpendicolari bisecanti) dei suoi lati si intersecano in uno stesso punto (circocentro).
Se gli assi dei lati del poligono non passano per un unico punto, il poligono non è inscrivibile in una circonferenza.
Vale anche il teorema inverso, se un poligono è inscritto in una circonferenza allora tutti gli assi dei suoi lati si intersecano in un unico punto ovvero nel centro della circonferenza.
La caratteristica di avere un unico punto di intersezione delle perpendicolari bisecanti dei lati, noto come circocentro, è soddisfatta da tutti i triangoli, da tutti i poligoni regolari e solo da alcuni poligoni irregolari, quelli che possono essere inscritti in una circonferenza.
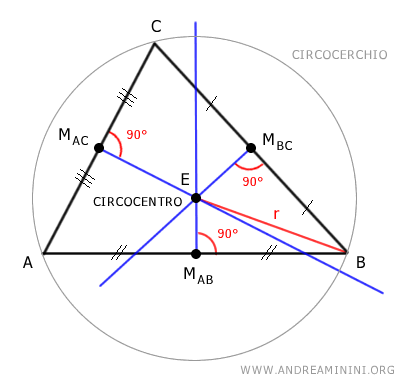
Un esempio pratico
Ad esempio, gli assi di un triangolo passano sempre per uno stesso punto chiamato circocentro del triangolo.
Se traccio una circonferenza centrata nel circocentro (E) con un opportuno raggio (r), la circonferenza passa per tutti i vertici del triangolo.
La dimostrazione
Per dimostrare il teorema considero un poligono con tutti gli assi dei suoi lati che passano per uno stesso punto O.
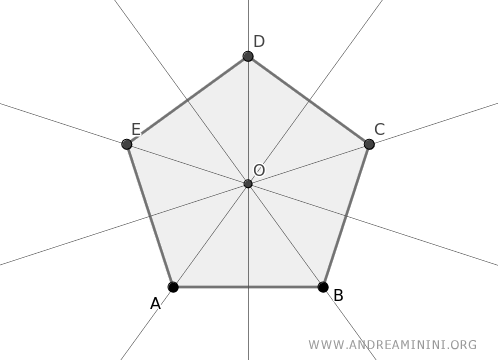
Dove per "asse" del lato intendo la retta perpendicolare bisecante al lato, ovvero la retta che passa per il punto medio del lato formando un angolo retto (90°).
Devo dimostrare che il poligono può essere inscritto in una circonferenza.
Per definizione l'asse è il luogo geometrico dei punti equidistanti dagli estremi di un segmento.
Quindi, i punti di un asse sono equidistanti dagli estremi di un lato del poligono.
Ad esempio, il punto P sull'asse del lato AB è equidistante dagli estremi A e B.
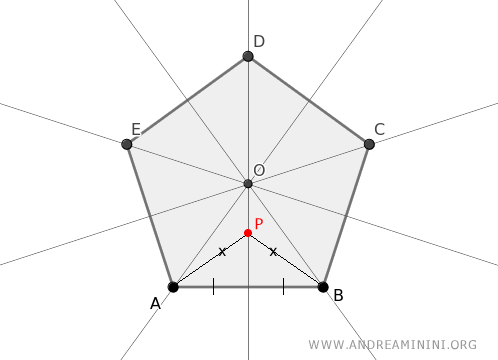
Questo significa che il punto di intersezione O, dove si intersecano gli assi, è equidistante da tutti i vertici del poligono.
In altre parole, la distanza d tra il punto O e qualsiasi vertice del poligono è la stessa.
$$ d = \overline{OA} = \overline{OB} = \overline{OC} = \overline{OD} = \overline{OE} $$
Pertanto, posso tracciare una circonferenza con centro O (circocentro) che ha per raggio la distanza d tra il punto O e un vertice qualsiasi del poligono.
Questa circonferenza passa per tutti i vertici del poligono, quindi è una circonferenza circoscritta al poligono.
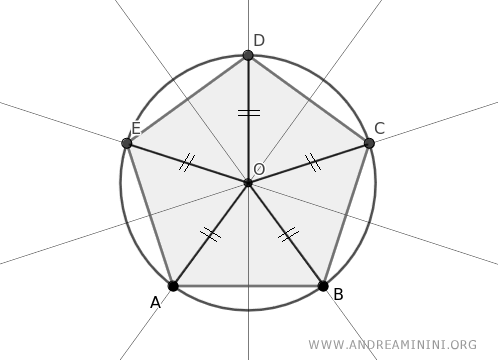
Questo dimostra che il poligono è inscritto in una circonferenza.
E così via.
