Il raggio di un cerchio circoscritto a un triangolo
Il raggio di un cerchio circoscritto a un triangolo è uguale al rapporto tra il prodotto dei lati (a·b·c) e il quadruplo dell'area (A) del triangolo $$ r = \frac{a \cdot b \cdot c}{4 \cdot A} $$ Dove a,b,c sono le lunghezze dei lati del triangolo mentre A è l'area del triangolo.
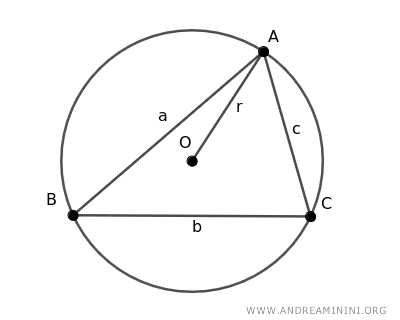
Questa formula è strettamente collegata al teorema di Herone che calcola l'area di un triangolo a partire dal semiperimetro.
$$ A=p \cdot (p−a) \cdot (p−b) \cdot (p−c) $$
Dove p è il semiperimetro del triangolo, 2p=a+b+c.
Se inserisco l'espressione dell'area A della formula di Herone nella formula per R, si stabilisce un legame diretto tra i lati del triangolo (a,b,c), il suo semiperimetro (p), e il raggio (r) del cerchio circoscritto.
$$ r = \frac{a \cdot b \cdot c}{4 \cdot A} = \frac{a \cdot b \cdot c}{4 \cdot p \cdot (p−a) \cdot (p−b) \cdot (p−c)} $$
Il raggio r del circocerchio posso collegarlo all'area A e ai lati del triangolo attraverso le relazioni geometriche che coinvolgono la circonferenza circoscritta e le proprietà dei triangoli. Per un approfondimento rimando alla dimostrazione.
Un esempio pratico
Prendo come esempio questa circonferenza che ha un raggio OA=3 con un triangolo inscritto qualsiasi ABC.
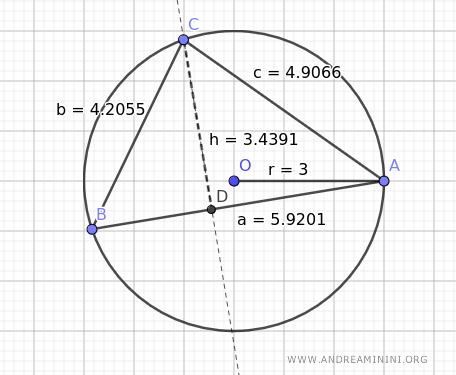
Verifico se la formula è vera
$$ r = \frac{a \cdot b \cdot c}{4 \cdot A} $$
Sostituisco le lunghezze dei lati a=5.9201, b=4.9066 e c=4.2055
$$ r = \frac{5.9201 \cdot 4.9066 \cdot 4.2055}{4 \cdot A} $$
$$ r = \frac{122.1586}{4 \cdot A} $$
L'area del triangolo si ottiene calcolando il semiprodotto della base per l'altezza
$$ A = \frac{a \cdot h}{2} = \frac{5.9201 \cdot 3.4391}{2} = 10.1799 $$
Sostituico il valore dell'area A=10.1799 del triangolo nella formula del raggio.
$$ r = \frac{122.1586}{4 \cdot 10.1799} \approx 3 $$
In questo modo ottengo la lunghezza del raggio r=3 della circonferenza circoscritta al triangolo.
Il risultato finale conferma la lunghezza effettiva del raggio data all'inizio dell'esempio.
Questo esempio pratico dimostra l'applicabilità e la correttezza della formula in un caso concreto.
La dimostrazione
Considero un cerchio con centro O e raggio OA.
Prendo tre punti distinti A, B, C sulla circonferenza e traccio i segmenti per formare un triangolo ABC.
Traccio il diametro (d) della circonferenza e l'altezza (h) del triangolo.
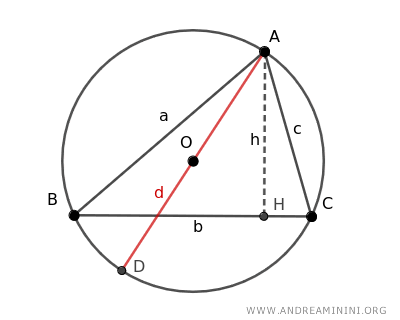
Si formano due triangoli rettangoli AHC e ABD.
- Il triangolo AHC è un triangolo rettangolo perché il lato h è l'altezza del triangolo ABC, quindi è perpendicolare ai segmenti BC e a HC.
- Il triangolo ABD è un triangolo rettangolo perché il lato AD coincide con il diametro del cerchio e ogni triangolo inscritto costruito sul diametro (ovvero su una semicirconferenza) è un triangolo rettangolo.
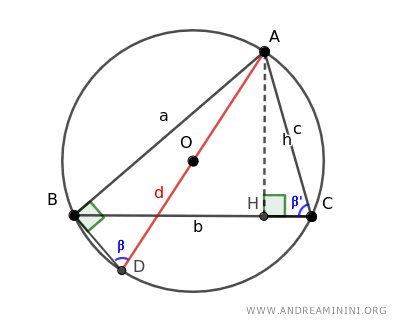
I triangoli AHC e ABD hanno due angoli congruenti.
- L'angolo retto (90°)
- Gli angoli acuti β e β' sono congruenti β≅β' perché sono angoli alla circonferenza che insistono sullo stesso arco AB.
Pertanto, secondo i criteri della similitudine dei triangoli, i triangoli AHC e ABD sono triangoli simili.
$$ AHC \approx ABD $$
Essendo simili, i due triangoli ABH hanno gli angoli congruenti e i lati proporzionali nello stesso ordine.
Pertanto, posso scrivere la proporzione.
$$ a : h = d: c $$
Sapendo che il diametro d=2r è due volte il raggio.
$$ a : h = 2r: c $$
Riscrivo la proporzione come frazione equivalente.
$$ \frac{a}{h} = \frac{2r}{c} $$
Ricavo il raggio
$$ r = \frac{ac}{2h} $$
Moltiplico e divido per b la frazione nel membro di destra.
$$ r = \frac{ac}{2h} \cdot \frac{b}{b} $$
$$ r = \frac{abc}{2hb} $$
Il prodotto hb è il doppio dell'area A=hb/2 del triangolo ABC. Quindi hb=2A.
$$ r = \frac{abc}{2 \cdot (2A)} $$
$$ r = \frac{abc}{4A} $$
Questo dimostra che il raggio del cerchio circoscritto a un triangolo ha una lunghezza uguale al rapportro tra il prodotto dei lati e il quadruplo dell'area del triangolo.
E così via.
