Teorema della retta perpendicolare al raggio e tangente a una circonferenza

Una retta tangente a una circonferenza è perpendicolare al raggio della circonferenza, e viceversa.

Se considero una circonferenza di centro O e raggio OP, la retta tangente nel punto P è perpendicolare al raggio.

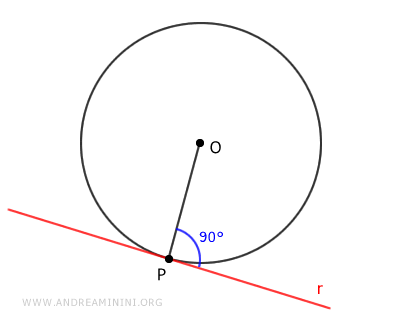
Vale anche il teorema inverso, se nel punto P di una circonferenza una retta è perpendicolare al raggio, allora è una retta tangente alla circonferenza nel punto P.

Nota. Questo accade perché ogni retta ha un'unica perpendicolare che passa per un suo punto P e la distanza minima tra un punto e una retta è sempre perpendicolare alla retta. Quindi, anche la retta tangente alla circonferenza nel punto P è una e una sola.

Dimostrazione

La dimostrazione è suddivisa in due parti, una per il teorema e l'altra per il teorema inverso.

A] Una retta tangente in un punto della circonferenza è perpendicolare al raggio

Per prima cosa, provo a dimostrare che una retta tangente a una circonferenza è anche perpendicolare al raggio.

Considero una circonferenza con centro O e raggio OP e una retta tangente nel punto P della circonferenza.

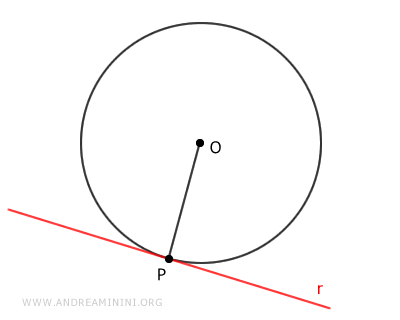
Per definizione, una retta tangente ha un solo punto in comune con la circonferenza.

Sapendo anche che in un punto della retta passa un'unica perpendicolare, deduco che la retta tangente abbia una e una sola perpendicolare nel punto P.

Secondo il teorema della distanza di una retta da una circonferenza, una retta è tangente alla circonferenza nel punto P quando la distanza tra la retta (r) e il centro (O) della circonferenza è uguale al raggio (OP).

$$ d(r,O) \cong \overline{OP} $$

 

Poiché la distanza (minima) tra una retta e un punto (O) è sempre perpendicolare alla retta, ossia forma un angolo retto (90°), deduco che anche il raggio è perpendicolare alla retta tangente.

$$ \overline{OP} \perp r $$

Inoltre, deduco che nel punto P passa una e una sola retta tangente.

B] Una retta perpendicolare al raggio in un punto della circonferenza è anche tangente alla circonferenza.

Considero una circonferenza con centro O e raggio OP.

Inoltre, assumo per ipotesi che una retta passa per il punto P ed è perpendicolare al raggio OP.

 

Sapendo che ogni retta ha un'unica perpendicolare che passa per un suo punto, deduco che non ce ne siano altre nel punto P.

La distanza più breve tra una retta e un punto qualsiasi (O) è sempre un segmento perpendicolare (90°) alla retta.

Quindi, il segmento OP misura anche la distanza tra la retta r e il punto O oltre al raggio.

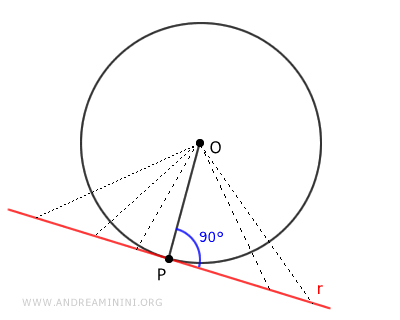
Secondo il teorema della distanza, quando la distanza di una retta dal centro della circonferenza coincide con il raggio, la retta passa per un solo punto della circonferenza ossia è una retta tangente.

Pertanto, la retta perpendicolare al raggio OP nel suo estremo P è anche una retta tangente alla circonferenza nello stesso punto P.

Come verificare matematicamente che la retta tangente sia perpendicolare al raggio

Per verificare matematicamente che una retta tangente a un cerchio sia perpendicolare al raggio del cerchio nel punto di tangenza, posso utilizzare la geometria analitica.

Preferisco spiegarlo direttamente con un esempio pratico.

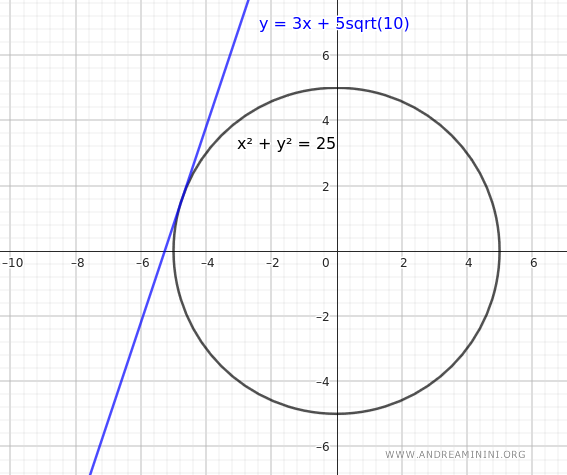
Considero un cerchio con centro \( O(0, 0) \) e raggio \( r = 5 \). L'equazione del cerchio è:

$$ x^2 + y^2 = 25 $$

Suppongo che la retta tangente abbia l'equazione:

$$ y = 3x + c $$

ovvero

$$ 3x - y + c = 0 $$

Per trovare il punto di tangenza, posso usare la condizione che la distanza dal centro del cerchio alla retta tangente deve essere pari al raggio del cerchio (r=5):

$$ d = \frac{|ax_0+by_0+c|}{\sqrt{a^2+b^2}} = r $$

$$ \frac{|3 \cdot 0 + (-1) \cdot 0 + c|}{\sqrt{3^2 + (-1)^2}} = 5 $$

$$ \frac{|c|}{\sqrt{9 +1}} = 5 $$

$$ \frac{|c|}{\sqrt{10}} = 5 $$

Semplificando ottengo:

$$ \frac{|c|}{\sqrt{10}} = 5 \quad \Rightarrow \quad |c| = 5\sqrt{10} $$

Quindi \( c = 5\sqrt{10} \) o \( c = -5\sqrt{10} \).

Ad esempio, scelgo \( c = 5\sqrt{10} \) e l'equazione della retta tangente diventa:

$$ y = 3x + 5\sqrt{10} $$

Per conferma disegno il grafico della circonfernza e della retta tangente

Il punto di tangenza \( T(x_1, y_1) \) soddisfa entrambe le equazioni:

$$ \begin{cases} y_1 = 3x_1 + 5\sqrt{10} \\ \\ x_1^2 + y_1^2 = 25 \end{cases} $$

Sostituendo \( y_1 \):

$$ \begin{cases} y_1 = 3x_1 + 5\sqrt{10} \\ \\ x_1^2 + (3x_1 + 5\sqrt{10})^2 = 25 \end{cases} $$

$$ \begin{cases} y_1 = 3x_1 + 5\sqrt{10} \\ \\ x_1^2 + 9 x_1^2 + 30 \sqrt(10) x_1 + 250 = 25 \end{cases} $$

$$ \begin{cases} y_1 = 3x_1 + 5\sqrt{10} \\ \\ 10x_1^2 + 30 \sqrt(10) x_1 + 225 = 0 \end{cases} $$

Risolvendo quest'ultima equazione trovo \( x_1 \) e quindi \( y_1 \).

Quindi, risolvo l'equazione di secondo grado e ottengo x₁= -1.5√ 10 ≈ -4.743

$$ \begin{cases} y_1 = 3x_1 + 5\sqrt{10} \\ \\ x_1 =  -1.5\sqrt{10} \approx - 4.743 \end{cases} $$

Nota. Questi sono i passaggi svolti per ottenere il valore di x₁. $$ x_1 = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a} $$ Dove \( a = 10 \), \( b = 30\sqrt{10} \), \( c = 225 \). $$ x_1 = \frac{-30\sqrt{10} \pm \sqrt{(30\sqrt{10})^2 - 4 \cdot 10 \cdot 225}}{2 \cdot 10} $$ $$
x_1 = \frac{-30\sqrt{10} \pm \sqrt{9000 - 9000}}{20} $$ $$ x_1 = \frac{-30\sqrt{10}}{20} $$ $$ x_1 = -1.5\sqrt{10}  ≈ -4.743 $$

Sostituisco x₁=-1.5√10 (circa -4.743) nella prima equazione e ottengo y₁=0.5√10 (circa 1.58)

$$ \begin{cases} y_1 = 3 \cdot ( -1.5\sqrt{10} ) + 5\sqrt{10} \\ \\ x_1 = -1.5\sqrt{10} \end{cases} $$

$$ \begin{cases} y_1 = -4.5\sqrt{10} + 5\sqrt{10} \\ \\ x_1 = -1.5\sqrt{10} \end{cases} $$

$$ \begin{cases} y_1 = y_1 = 0.5\sqrt{10} \approx 1.58 \\ \\ x_1 = -1.5\sqrt{10} \approx -4.743 \end{cases} $$

Pertanto, il punto di tangenza P si trova alle coordinate (x₁;y₁)=(-1.5√10 ; 0.5√10 ) ovvero circa (-4.743;1.58)

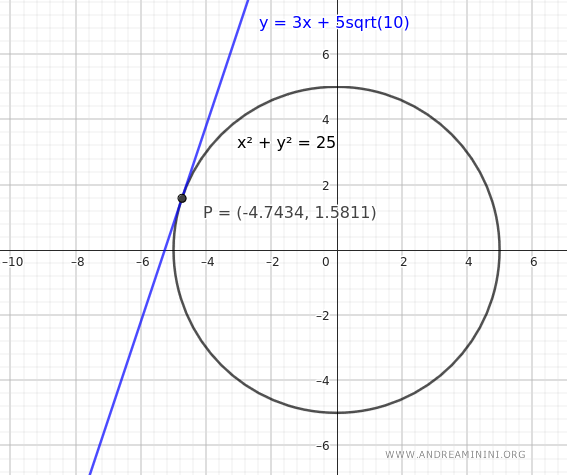
Ora posso trovare l'equazione del raggio che passa per il centro del cerchio \( O(0, 0) \) e per il punto di tangenza P.

L'equazione di una retta passante per due punti \( (x_1, y_1) \) e \( (x_2, y_2) \) è data da:

$$ y - y_1 = m (x - x_1) $$

dove \( m \) è la pendenza della retta, calcolata come:

$$ m = \frac{y_2 - y_1}{x_2 - x_1} $$

In questo caso, i punti sono \( O(0, 0) \) e \( T(-4.743, 1.58) \).

Quindi, la pendenza \( m \) è:

$$  m = \frac{0.5\sqrt{10}-0}{-1.5\sqrt{10}-0} =  \frac{0.5\sqrt{10}}{-1.5\sqrt{10}} = -\frac{1}{3}  \approx -0.333 $$

Ora posso scrivere l'equazione della retta che passa per il raggio e per il punto di tangenza.

$$ y - 0 = - \frac{1}{3} (x - 0) $$

Quindi l'equazione della retta del raggio è:

$$ y = - \frac{1}{3} x $$

Per completezza aggiungo anche la retta y=-1/3x (rossa)  che contiene il raggio OP nel grafico.

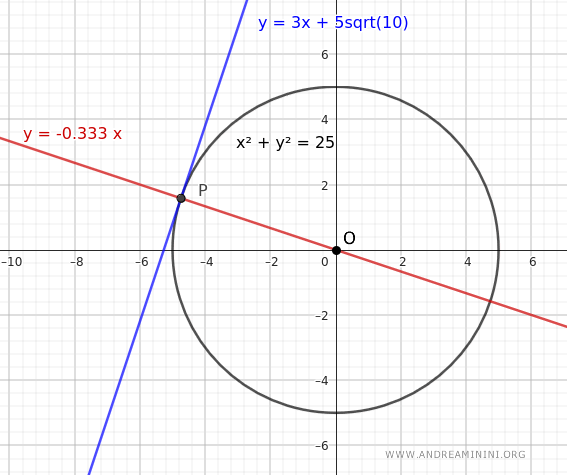
A questo punto, devo verificare che il raggio sia effettivamente perpendicolare alla tangente.

Sapendo che due rette sono perpendicolari se il prodotto delle loro pendenze è \( -1 \), quindi devo verificare che:

$$ m_{\text{raggio}} \cdot m_{\text{tangente}} = -1 $$

La pendenza della tangente è \( 3 \) mentre quella del raggio è \( - \frac{1}{3} \).

$$ -\frac{1}{3} \cdot 3 = -1 $$

Il risultato è -1, pertanto posso confermare che il raggio è effettivamente perpendicolare alla tangente.

Questo dimostra matematicamente che ogni retta tangente è perpendicolare al raggio nel punto di tangenza.

E così via.