Pi greco
Pi greco è un numero irrazionale che indica il rapporto tra una qualsiasi circonferenza (C) e il suo diametro (d). Il valore approssimativo è $$ \pi = \frac{C}{d} = 3,1415926535 $$
Poiché π (pi greco) è un numero irrazionale, non può essere rappresentato come una frazione esatta e ha una rappresentazione decimale infinita e non periodica.
La lettera π dell'alfabeto greco viene utilizzata in quanto iniziale della parola "perimetro". Infatti, attraverso questo valore, si può determinare la circonferenza C=2πr ossia il perimetro del cerchio.
$$ C = \pi \cdot d = \pi \cdot 2r $$
Dove r è il raggio della circonferenza ed è sempre uguale alla metà della diagonale d=2r.
Fu il matematico greco Archimede a determinare per la prima volta il valore di pi greco con precisione fino alle prime due cifre decimali, utilizzando poligoni a 96 lati come riferimento.
La storia del pi greco
L'origine del numero 3,14, meglio conosciuto come Pi greco (π) risale alle prime civiltà della storia e affonda le sue radici nella geometria antica.
Fin da subito ci si accorse che il rapporto tra la circonferenza di un cerchio e il suo diametro è un numero costante.
In altre parole, non importa quanto grande o piccolo sia un cerchio, se dividi la lunghezza della sua circonferenza per il diametro, otterrai sempre approssimativamente il valore di π, che è circa 3,14.
Le prime approssimazioni risalgono ai babilonesi e agli egizi.
I babilonesi utilizzavano un valore approssimativo di 3 1/8 (3,125) per π, mentre una stima egizia che si trova nel papiro di Rhind, indica un valore di circa 3,16.
Queste prime stime erano sorprendentemente vicine al vero valore di π, considerando i metodi rudimentali che avevano a disposizione per misurare e calcolare.
Furono però gli antichi greci a perfezionare il calcolo attraverso le figure di matematici come Archimede.
Archimede di Siracusa, vissuto nel III secolo a.C., portò il calcolo di π a un elevato livello di precisione, attraverso un metodo geometrico ingegnoso che oggi conosciamo come il metodo di esaustione.
Archimede utilizzò dei poligoni regolari inscritti e circoscritti per approssimare la circonferenza di un cerchio.
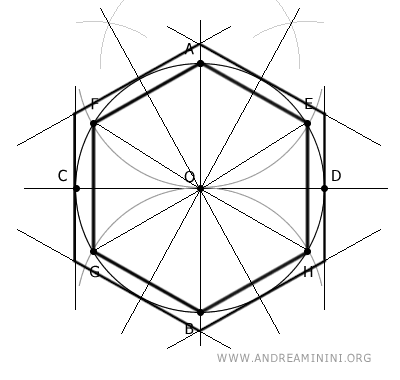
Più specificamente, iniziò con esagoni raddoppiando ripetutamente il numero di lati dei poligoni fino ad arrivare a un poligono di ben 96 lati!
Con questo metodo, Archimede riuscì a stabilire che il valore di π si trovava tra 3 1/7 (circa 3,1429) e 3 10/71 (circa 3,1408), che è un'approssimazione sorprendentemente accurata per quei tempi.
Oggi conosciamo questa costante matematica con la lettera "pi greco" ( π ).
In realtà, questa associazione è molto più recente. Fu introdotta molto più tardi, nel 1706, da William Jones, un matematico gallese e dal matematico svizzero Leonhard Euler nel corso del XVIII secolo.
Nota. Con l'avvento dei computer, il numero π è stato calcolato con precisione fino a milioni di cifre dopo la virgola. E' una sfida matematica che continua ancora oggi e spesso è usata per testare i limiti della computazione numerica dei computer e della teoria dei numeri.
Come calcolare il pi greco
La ricerca del pi greco parte dalla necessità di calcolare il perimetro di un cerchio, ossia di trovare la lunghezza della circonferenza.
Il perimetro della circonferenza è C=2πr
Costruisco un esagono regolare inscritto nella circonferenza.
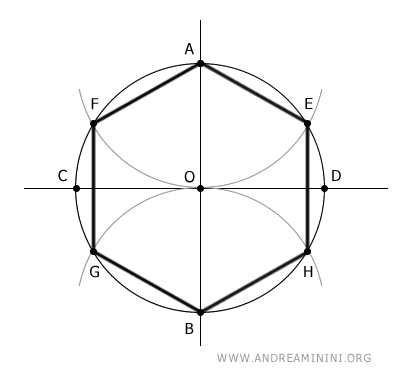
Nota. Per disegnare un esagono inscritto in una circonferenza basta tracciare gli assi perpendicolari e disegnare due archi con lo stesso raggio della circonferenza.
La distanza tra il centro della circonferenza (O) e un vertice qualsiasi dell'esagono inscritto è uguale al raggio.
$$ \overline{OA} = \overline{OB} = ... = r $$
Poiché l'esagono ha sei lati e la somma degli angoli interni di un cerchio è 360°, l'angolo al centro ∠AOE corrispondente a un sesto della circonferenza è 360°/6=60°.
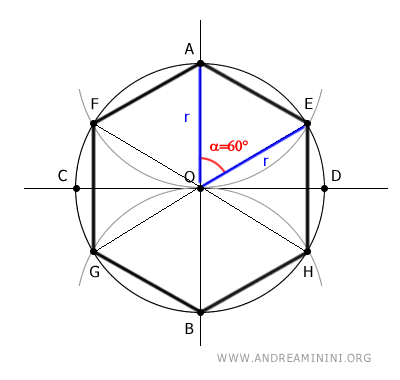
Il triangolo OAE è un triangolo isoscele perché ha due lati congruenti OA≅OE in quanto hanno entrambi una lunghezza pari al raggio r della circonferenza OA=r e OE=r.
Sapendo che in un triangolo isoscele gli angoli alla base sono congruenti, deduco che gli angoli β≅γ del triangolo OAE sono congruenti.
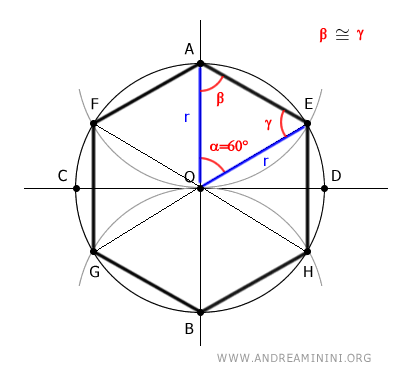
Sapendo che un angolo del triangolo OAE è uguale a 60° e la somma degli angoli interni di un triangolo è sempre uguale a 180°, deduco che la somma degli angoli restanti sia uguale a 120°
$$ 180° - \alpha = \beta + \gamma $$
$$ 180° - 60° = \beta + \gamma $$
$$ 120° = \beta + \gamma $$
Poiché gli angoli β≅γ sono congruenti, deduco che ciascuno di loro sia pari a 60°
$$ \beta = \gamma = 60° $$
Il triangolo OAE ha tutti gli angoli congruenti β≅γ≅α≅60°.
Quindi, il triangolo OAE è anche un triangolo equilatero, ovvero ha tutti i lati congruenti.
$$ \overline{OA} \cong \overline{OE} \cong \overline{AE} $$
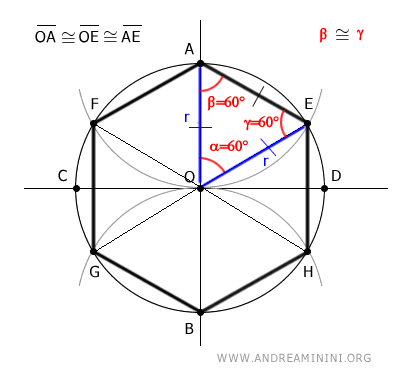
Sapendo che OA=OE=r sono uguali al raggio, deduco che anche il lato dell'esagono AE=r è uguale al raggio della circonferenza.
$$ \overline{AE} = r $$
Pertanto, in un esagono regolare inscritto in una circonferenza, il perimetro (P) dell'esagono è uguale a sei volte il raggio della circonferenza.
$$ P = 6r $$
Essendo un esagono inscritto nella circonferenza, il suo perimetro è inferiore a quello della circonferenza.
$$ 6 r < 2 \pi r $$
Semplifico dividendo per due entrambi i membri della disequazione
$$ 3 r < \pi r $$
Poi divido per r entrambi i membri
$$ 3 < \pi $$
Pertando, deduco che il valore di pi greco è maggiore di 3.
Ora costruisco un esagono regolare circoscritto alla circonferenza.
Per farlo traccio le rette passanti per il centro e per i punti medi dei sei triangoli equilateri che compongono l'esagono inscritto nella circonferenza.
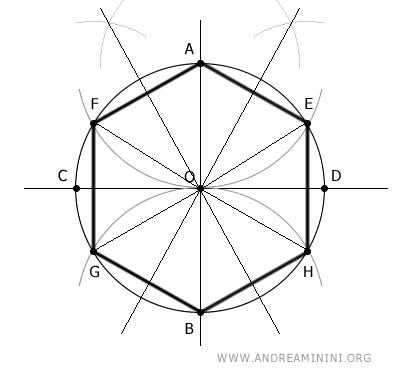
Poi traccio le rette tangenti alla circonferenza che intersecano le rette passanti per i punti medi.
Basta disegnare una retta perpendicolare alle rette precedenti nei vari punti medi.
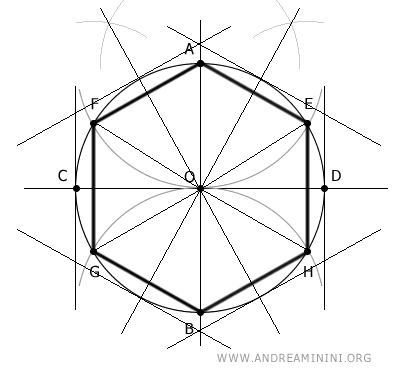
Il risultato finale è un esagono circoscritto.

Per continuare lo studio con maggiore chiarezza, riporto il disegno con il solo esagono circoscritto.
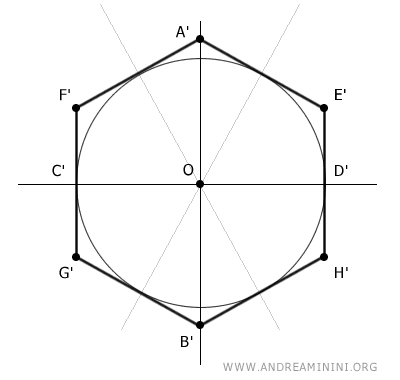
Traccio i segmenti tra l'origine e i vertici dell'esagono A', B', E', F', G', H'.
In questo modo suddivido l'esagono in sei triangoli congruenti.
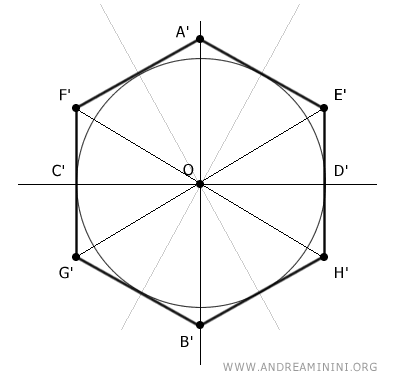
Considero il triangolo OE'H'.
Anche in questo caso l'esagono ha sei lati e la somma degli angoli interni di un cerchio è 360°, quindi l'angolo al centro ∠E'OH' corrisponde a un sesto della circonferenza è 360°/6=60°.
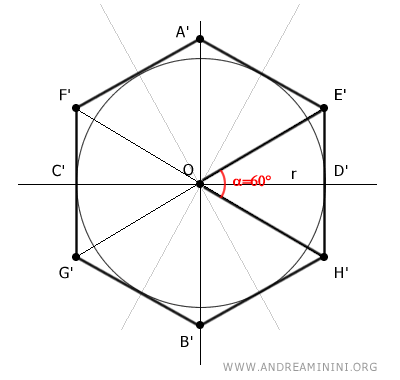
In questo caso il raggio della circonferenza coincide con il segmento OD' ossia con l'altezza del triangolo OE'H',
Il triangolo OE'H' è composto da due triangoli rettangolo OE'D' e OH'D' con gli angoli uguali a 30°, 60°, 90°
Quindi, posso calcolare la lunghezza del cateto E'D' e H'D' usando la formula del triangolo rettangolo con angoli acuti 30° e 60°
$$ \overline{E'D'} = \frac{ \overline{OD'} \sqrt{3} }{3} $$
$$ \overline{H'D'} = \frac{ \overline{OD'} \sqrt{3} }{3} $$
Pertanto, sapendo che il lato E'H'=E'D'+H'D' ottengo:
$$ \overline{E'H'} = 2 \cdot \frac{ \overline{OD'} \sqrt{3} }{3} $$
Il segmento OD' è il raggio della circonferenza (r)
$$ \overline{E'H'} = 2 \cdot \frac{ r \cdot \sqrt{3} }{3} $$
Una volta ottenuta la lunghezza del lato dell'esagono in base al raggio, calcolo il perimetro dell'esagono regolare.
Il perimetro P dell'esagono regolare è uguale a sei volte il lato E'H'
$$ P = 6 \cdot \overline{E'H'} $$
$$ P = 6 \cdot 2 \cdot \frac{ r \cdot \sqrt{3} }{3} $$
$$ P = 12 \cdot \frac{ r \cdot \sqrt{3} }{3} $$
$$ P = 4 \cdot r \cdot \sqrt{3} $$
Essendo un esagono circoscritto alla circonferenza, il suo perimetro è maggiore rispetto alla circonferenza C=2πr
$$ P > C $$
$$ 4 \cdot r \cdot \sqrt{3} > 2 \pi \cdot r $$
Ora semplifico dividendo entrambi i membri della disequazione per r
$$ 4 \cdot \sqrt{3} > 2 \pi $$
Poi ricavo pi greco dividendo entrambi i membri per 2
$$ 2 \cdot \sqrt{3} > \pi $$
Il prodotto 2√3 è all'incirca 3,46.
$$ 3,46 > \pi $$
Pertanto, il valore di pi greco è minore di 3,46.
In conclusione, grazie al perimetro dell'esagono inscritto e circoscritto si comprende che il valore di pi greco è maggiore di 3 e minore di 3,46.
Nota. Questo dimostra che la lunghezza della circonferenza è l'elemento che separa la classe dei perimetri dei poligoni regolari inscritti da quella dei poligoni regolari circoscritti alla circonferenza.
Ripetendo la stessa operazione usando poligoni regolari con più lati, il calcolo diventa più preciso.
Basta considerare che Archimede riuscì a trovare le prime due cifre decimali del valore pi greco utilizzando un poligono con 96 lati.
Osservazioni
Alcune osservazioni e note a margine sul pi greco.
- Come ricordarsi il pi greco?
Generalmente ci si ricorda del pi greco come 3.14 ma pochi ricordano anche le successive cifre decimali. Spesso, per ricordarle si ricorre a qualche stratagemma mnemonico. Ad esempio, per ricordare a memoria un certo numero di cifre si trova una frase o una filastrocca e si contano le lettere di ciascuna parola. Ad esempio, in italiano una frase mnemnica è la seguente: "Ave o Roma o Madre gagliarda di latine virtù che tanto luminoso splendore prodiga spargesti con la tua saggezza".

E così via.
