Cerchio

Un cerchio è una figura geometrica piana definita dall'insieme di tutti i punti che appartengono a una circonferenza e da quelli contenuti al suo interno.

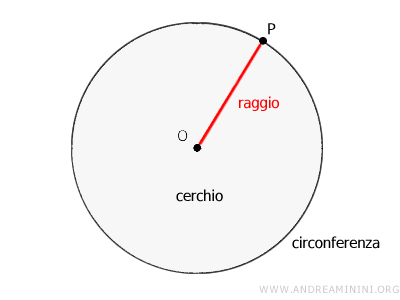
Un cerchio si può definire anche come l'insieme di tutti i punti in un piano che hanno una distanza dal centro del cerchio O inferiore o uguale al raggio (r).

Dove il raggio è il segmento che congiunge il centro del cerchio (O) con uno dei suoi punti della circonferenza.

 

Il cerchio è stato oggetto di studio per migliaia di anni. Fin dalle prime civiltà, come gli egizi, i babilonesi e i greci, l'uomo ha studiato e utilizzato il cerchio in vari contesti, dalla costruzione degli edifici all'astronomia.

Le caratteristiche del cerchio

La circonferenza è il perimetro del cerchio.

La lunghezza di una circonferenza C si calcola moltiplicando il diametro (d) per la costante pi greco.

$$ C = \pi \cdot d $$

Poiché il diametro è il doppio del raggio d=2r, posso scrivere la formula anche in questa formula equivalente C=2πr, dove r è il raggio del cerchio

$$ C = 2 \pi \cdot r $$

La costante π (pi greco) è il rapporto tra la circonferenza di un cerchio e il suo diametro. E' una costante matematica uguale all'incirca a 3,14 ed è indipendente dalle dimensioni del cerchio, perché il rapporto fra la lunghezza di una qualsiasi circonferenza e quello del diametro è un numero costante.

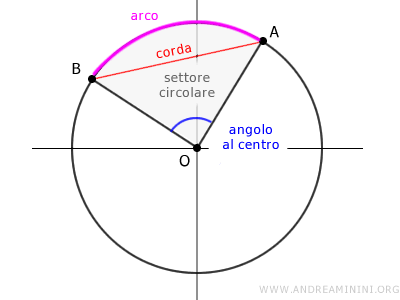
Un arco è una parte della circonferenza del cerchio.

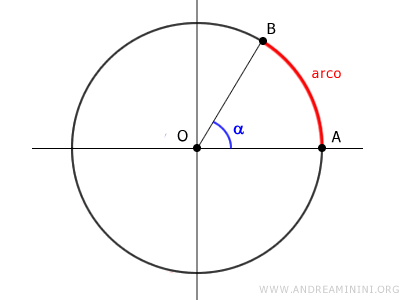
La lunghezza di un arco di circonferenza (L) è direttamente proporzionale all'ampiezza dell'angolo (α) al centro della circonferenza.

$$ L:C = \alpha : 360° $$

In altre parole, la lunghezza dell'arco (L) sta alla lunghezza della circonferenza (C) come l'angolo α sta a 360° (angolo giro).

L'area di un cerchio si ottiene moltiplicando il quadrato del raggio (r) per pi greco π≅3,14

$$ A = \pi r^2 $$

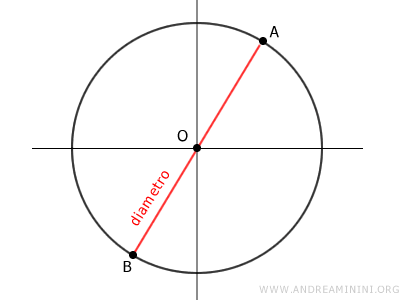
Il diametro è un segmento che passa attraverso il centro del cerchio e tocca entrambi i lati della circonferenza. È il doppio della lunghezza del raggio (r).

Una corda è un segmento che collega due punti sulla circonferenza ma non passa necessariamente per il centro.

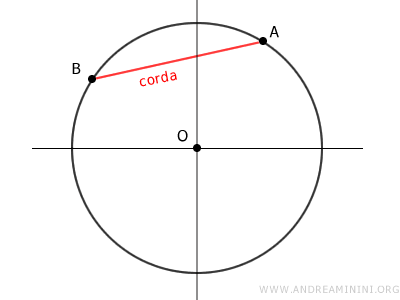
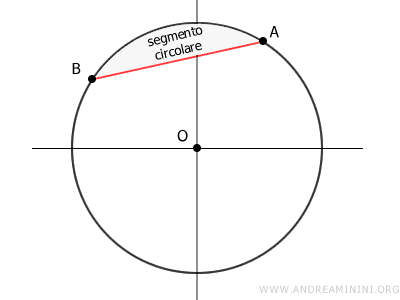
Ogni corda divide il cerchio in due parti, ciascuna delle quali è detta segmento circolare o segmento circolare a una base.

Se il segmento circolare è minore di un semicerchio, l'area del segmento circolare è uguale alla differenza tra l'area del settore circolare corrispondente e l'area del triangolo OAB se il settore.

 

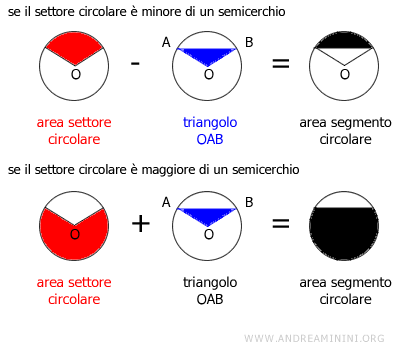
Viceversa, se il segmento circolare è maggiore di un semicerchio, l'area del segmento circolare è uguale alla somma tra il settore circolare e l'area del triangolo OAB.

Dove per semicerchio si intende la metà del cerchio.

L'insieme dei punti del cerchio compreso tra due corde parallele è, invece, detto segmento circolare a due basi.

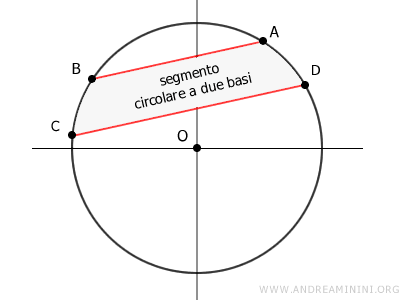
L'area del segmento circolare a due basi si ottiene sottraendo dall'area (A) del cerchio l'area dei due segmenti a una base ottenuti con le corde AB e CD.

Un settore (o settore circolare) è una parte del cerchio delimitata da due raggi e dalla circonferenza.

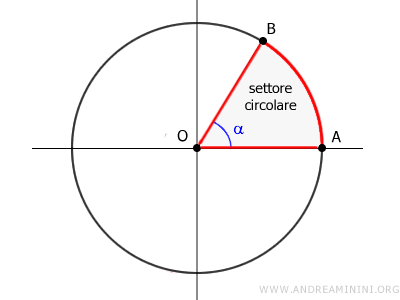
L'area del settore circolare è direttamente proporzionale all'angolo α al centro della cerchio.

$$ A_s : A = \alpha : 360° $$

In altre parole, l'area del settore circolare A_s sta all'area del cerchio A, come l'angolo α sta all'angolo giro (360°).

Si parla di corona circolare per indicare la superficie compresa tra due circonferenze concentriche, che hanno in comune lo stesso centro (O) ma hanno raggio diverso.

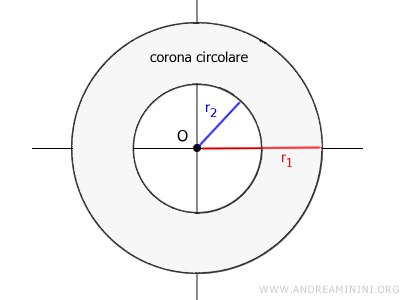
L'area della corona circolare si ottiene sottraendo l'area del cerchio minore dall'area del cerchio maggiore.

$$ A_c = \pi \cdot r_1^2 - \pi \cdot r_2^2 $$

Le formule del cerchio

Le principali formule per calcolare le misure del cerchio

• Circonferenza
  La circonferenza (C) è uguale al doppio prodotto del raggio (r) per 3.14 (π) $$ C=2r \cdot \pi $$ Sapendo che la diagonale è uguale al doppio del raggio, la formula equivalente è la seguente $$ C = d \cdot \pi $$
• Area
  L'area del cerchio è uguale al prodotto tra il quadrato del raggio per 3.14 (π) $$ A = r^2 \cdot \pi $$
• Lunghezza dell'arco
  La lunghezza dell'arco (L) è direttamente proporzionale all'ampiezza dell'angolo (α) corrispondente $$ L:C = α:360° $$ Quindi la lunghezza dell'arco si ottiene con la seguente formula $$ L = \frac{ \alpha \cdot C }{360} $$
• Area di un settore
  L'area di un settore A_s è direttamente proporzionale all'ampiezza dell'angolo (α) $$ A_s : A = α:360° $$ Quindi, l'area di un settore si ottiene con la seguente formula $$ A_s = \frac{ \alpha \cdot A } {360} $$
• Area della corona circolare
  L'area della corona circolare Ac si calcola sottraendo l'area del cerchio minore dall'area del cerchio maggiore. $$ A_c = \pi \cdot r_1^2 - \pi \cdot r_2^2 = \pi \cdot (r_1^2 - r_2^2) $$

Osservazioni

Alcune osservazioni sulle circonferenze

• Una cerchio è una figura convessa, perché presi due punti qualsiasi del cerchio, il segmento che li unisce è interamente contenuto dentro la figura.

  Dimostrazione. La definizione di una figura convessa è che, per ogni coppia di punti all'interno della figura, il segmento che li congiunge è completamente contenuto all'interno della figura stessa. Per dimostrarlo considero due punti qualsiasi A e B del cerchio e il segmento AB che li congiunge. Ci sono due situazioni possibili
  1] I punti A e B appartengono allo stesso diametro
  Se i due punti A e B appartengono allo stesso diametro, anche il segmento AB è minore o uguale al diametro, poiché non può essere più lungo del diametro stesso.Quindi, il segmento AB è sicuramente interno al cerchio.
  
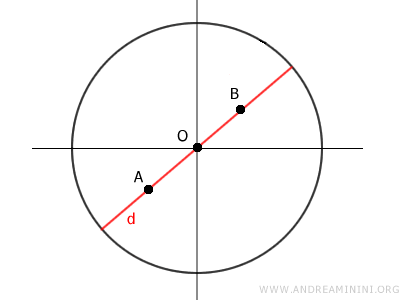
  2] I punti A e B non appartengono allo stesso diametro.
  Se i due punti A e B non appartengono allo stesso diametro, costruisco un triangolo OAB, dove O è il centro del cerchio.
  
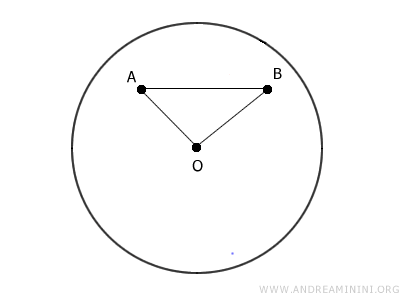
  A questo punto prendo come riferimento un punto qualsiasi C del segmento AB e dimostro che il segmento OC è sempre più corto di almeno uno tra OA e OB.
  2A] Se il segmento OC non è perpendicolare al lato AB, allora forma un angolo ottuso e un angolo acuto sul segmento AB. In un triangolo un angolo ottuso γ (90°<α<180°) è sempre l'angolo maggiore del triangolo.
  
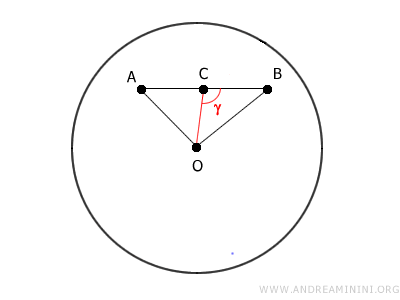
  Sapendo che il lato maggiore del triangolo è il lato opposto dell'angolo maggiore, deduco che il segmento OC è sempre inferiore al lato OA (nel triangolo OAC) oppure al lato OB (nel triangolo OBC). Ad esempio, nella figura precedente il segmento OC è inferiore al lato OB del triangolo OBC. $$ \overline{OC} < \overline{OA} $$ $$ \overline{OC}<\overline{OB} $$ I punti A e B sono due punti del cerchio, quindi i segmenti OA e OB non possono avere una lunghezza superiore al raggio del circonferenza (r) $$ \overline{OC} < \overline{OA} \le r $$ $$ \overline{OC}<\overline{OB} \le r $$ Pertanto, da questo deduco deduco che il segmento OC è interamente composto da punti appartenenti al cerchio.
  2B] Se il segmento è perpendicolare al lato AB, allora forma due triangoli rettangoli OAC e OBC. In entrambi i casi OC è un cateto di un triangolo rettangolo, pertanto è inferiore all'ipotenusa OA e OB.
  
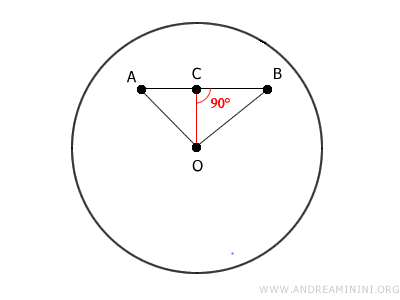
  Sapendo che i segmenti OA e OB non possono essere maggiori del raggio della circonferenza (r) deduco che anche in questo caso OC è un segmento inferiore al raggio. $$ \overline{OC} < \overline{OA} \le r $$ $$ \overline{OC}<\overline{OB} \le r $$ Quindi OC è interamente contenuto nel cerchio. In conclusione, qualunque punto C del segmento AB io prenda, il segmento OC è sempre contenuto nel cerchio, dimostrando così che il cerchio è una figura piana convessa.

• I principi di congruenza in un cerchio
  All'interno di una circonferenza, se si osserva la congruenza tra: due corde, due archi, due settori circolari, due segmenti circolari o due angoli al centro, allora tutte le altre figure menzionate saranno anch'esse congruenti. Questa relazione esiste perché queste entità sono intrinsecamente collegate in una corrispondenza uno a uno. Ad esempio, un determinato angolo al centro corrisponde a un arco, e viceversa.
  

E così via