Le circonferenze tangenti

Due circonferenze sono dette circonferenze tangenti se hanno un solo punto in comune.

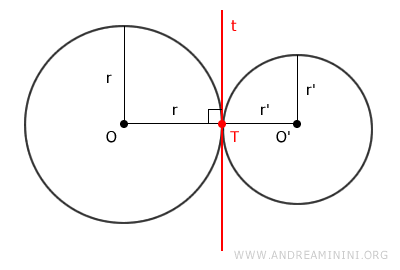
Il punto in comune è detto punto di tangenza o punto di contatto.

Due circonferenze possono essere tangenti in due modi:

• Circonferenze tangenti internamente
  Due circonferenze sono tangenti internamente se una circonferenza è all'interno dell'altra e toccano in un solo punto. Questo si verifica quando il centro di una circonferenza è situato all'interno dell'altra.
  
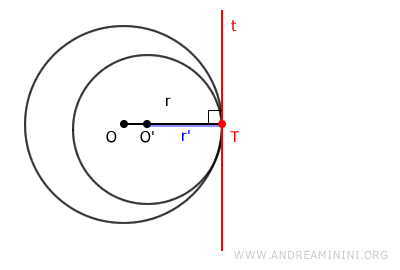
  Se i raggi delle due circonferenze sono \( r_1 \) e \( r_2 \) e le distanze tra i loro centri è \( d \), la condizione che deve essere soddisfatta per essere tangenti internamente è: \[ d = |r_1 - r_2| \]

  Calcolo della distanza tra i centri. Per calcolare la distanza tra i centri si utilizza la formula della distanza euclidea tra due punti del piano \[ d = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2} \]  Dove \( (x_1, y_1) \) e \( (x_2, y_2) \) sono le coordinate dei centri \( C_1 \) e \( C_2 \) delle due circonferenze nel piano cartesiano.

• Circonferenze tangenti esternamente
  Questo avviene quando il centro di ciascuna circonferenza si trova all'esterno dell'altra. Questo significa che il punto di tangenza si trova tra le due circonferenze, sulla linea che congiunge i centri delle due circonferenze.
  
  In questo caso, per essere tangenti esternamente la somma dei raggi r₁+r₂ deve essere uguale alla distanza (d) tra i centri delle due circonferenze:   \[ d = r_1 + r_2 \]

In entrambi i casi le circonferenze tangenti hanno un punto T in comune e la stessa retta tangente t.

Come trovare il punto di tangenza

Il punto di tangenza \( T \) si trova lungo la linea che unisce i due centri.

Se le circonferenze sono tangenti esternamente, le coordinate di \( T \) possono essere trovate usando la proporzione tra i raggi e la distanza \( d \):

$$ T = \left( x_1 + \frac{r_1}{r_1 + r_2}(x_2 - x_1), y_1 + \frac{r_1}{r_1 + r_2}(y_2 - y_1) \right) $$

Se le circonferenze sono tangenti internamente, le coordinate di \( T \) possono essere trovate usando la proporzione inversa tra i raggi e la distanza \( d \):

$$ T = \left( x_1 + \frac{r_1}{r_1 - r_2}(x_2 - x_1), y_1 + \frac{r_1}{r_1 - r_2}(y_2 - y_1) \right) $$

In alternativa, posso costruire un sistema di equazioni con le due equazioni delle circonferenze. $$ \begin{cases} (x - x_1)^2 + (y - y_1)^2 = r_1^2 \\ \\  (x - x_2)^2 + (y - y_2)^2 = r_2^2 \end{cases} $$ ovvero  $$ \begin{cases} x^2+y^2 +ax+by+c=0 \\ \\  x^2+y^2+a'x+b'y+c' = 0 \end{cases} $$ Poi risolvere il sistema con il metodo della riduzione, sottraendo la prima equazione alla seconda.  $$ \begin{cases} x^2+y^2 +ax+by+c=0 \\ \\  (a'-a)x+(b'-b)y+(c'-c) = 0 \end{cases} $$ La seconda equazione è l'asse radiale delle due circonferenze che, nel caso delle circonferenze tangenti, coincide con la retta tangente tra le due circonferenze. A questo punto basta risolvere il sistema per trovare i valori delle coordinate x e y del punto di tangenza.  

Una volta noto il punto di tangenza \( T \) la retta tangente può essere trovata anche utilizzando la formula delle tangenti alla circonferenza.

L'equazione della retta tangente alla circonferenza \( (x - x_0)^2 + (y - y_0)^2 = r^2 \) con centro \( C(x_0, y_0) \) e raggio \( r \) nel punto \(T = (x_T, y_T)\) è:

$$ (x_T - x_0)(x - x_0) + (y_T - y_0)(y - y_0) = r^2 $$

Un esempio pratico

Considero due circonferenze

$$ C_1 :  x^2+y^2-2x-9=0 $$

$$ C_2: x^2+y^2+4x-2y-35=0 $$

Il centro e il raggio della prima circonferenza si trovano conoscendo i coefficienti a=-2, b=0 e c=-9

$$ C_1 ( -\frac{a}{2}; -\frac{b}{2} = ( -\frac{(-2)}{2}; -\frac{0}{2} = ( 1;0) $$

$$ r_1 = \sqrt{ ( -\frac{a}{2})^2 + ( -\frac{b}{2})^2 } - c = \sqrt{1-0 - (-9)} = \sqrt{10} $$

Con lo stesso procedimento trovo il centro e il raggio della seconda circonferenza, in questo caso i coefficienti sono a=4, b=-2 e c=-35

$$ C_2 ( -\frac{a}{2}; -\frac{b}{2} = ( -\frac{(4)}{2}; -\frac{-2}{2} = ( -2;1) $$

$$ r_2 = \sqrt{ ( -\frac{a}{2})^2 + ( -\frac{b}{2})^2 } - c = \sqrt{(-2)^2+(1)^2 - (-35)} = \sqrt{4+1+35} = \sqrt{40} $$

Una volta note le coordinate dei centri $ C_1(1;0) $ e $ C_2 (-2,1) $ calcolo la distanza euclidea tra i due punti

$$ d = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2} $$

$$ d = \sqrt{(-2 - 1)^2 + (1 - 0)^2} $$

$$ d = \sqrt{(-3)^2 + (1)^2} $$

$$ d = \sqrt{9 + 1} $$

$$ d = \sqrt{10} $$

Calcolo la somma dei raggi e la differenza assoluta tra i raggi

$$ r_1+ r_2 = \sqrt{10} + \sqrt{40} = \sqrt{10} + \sqrt{4 \cdot 10} = \sqrt{10} + 2 \sqrt{10} = 3 \sqrt{10}$$

$$ | r_1 - r_2 | = | \sqrt{10} - \sqrt{40} | =  | \sqrt{10} - 2 \sqrt{10} | = | - \sqrt{10} | = \sqrt{10} $$

In questo caso la distanza tra i centri $ d = \sqrt{10} $ è uguale al valore assoluto della differenza tra raggi

$$ d = | r_1 - r_2 | = \sqrt{10} $$

Pertanto, le due circonferenze sono internamente tangenti.

Il punto di tangenza si trova a queste coordinate:

$$ T = \left( x_1 + \frac{r_1}{r_1 - r_2}(x_2 - x_1), y_1 + \frac{r_1}{r_1 - r_2}(y_2 - y_1) \right) $$

I raggi delle due circonferenze sono $ r_1 = \sqrt{10} $ e $ r_2 = \sqrt{40} $

$$ T = \left( x_1 + \frac{ \sqrt{10} }{\sqrt{10} - \sqrt{40}}(x_2 - x_1), y_1 + \frac{\sqrt{10}}{\sqrt{10} - \sqrt{40}}(y_2 - y_1) \right) $$

Le coordinate dei centri delle due circonferenze sono $ C_1(x_1,y_1)=(1,0) $ e $ C_2(x_2,y_2)=(-2,1) $

$$ T = \left( 1 + \frac{ \sqrt{10} }{\sqrt{10} - \sqrt{40}}(-2 - 1), 0 + \frac{\sqrt{10}}{\sqrt{10} - \sqrt{40}}(1 - 0) \right) $$

$$ T = \left( 1 + \frac{ \sqrt{10} }{\sqrt{10} - 2 \sqrt{10}}(-3), 0 + \frac{\sqrt{10}}{\sqrt{10} - 2\sqrt{10}}(1) \right) $$

$$ T = \left( 1 + \frac{ \sqrt{10} }{- \sqrt{10}}(-3), 0 + \frac{\sqrt{10}}{\sqrt{10} - 2\sqrt{10}}(1) \right) $$

$$ T = \left( 1 + \frac{ \sqrt{10} }{- \sqrt{10}}(-3), 0 + \frac{1}{1 - 2} \right) $$

$$ T = \left( 1 + 3, 0 -1 \right) $$

$$ T = \left(4, -1 \right) $$

Una volta noto il punto di tangenza $ T = (4,-1) $ posso trovare anche l'equazione della retta tangente.

$$ (x_T - x_0)(x - x_0) + (y_T - y_0)(y - y_0) = r^2 $$

$$ (4 - x_0)(x - x_0) + (-1 - y_0)(y - y_0) = r^2 $$

Considero il centro e il raggio di una delle due circonferenze, in genere la più semplice, ad esempio $ C_1( 1;0) $ e  $ r_1 = \sqrt{10} $

$$ (4 - 1)(x - 1) + (-1 - 0)(y - 0) = ( \sqrt{10} )^2 $$

$$ 3 (x - 1) -y = 10 $$

$$ 3x -3 -y - 10= 0 $$

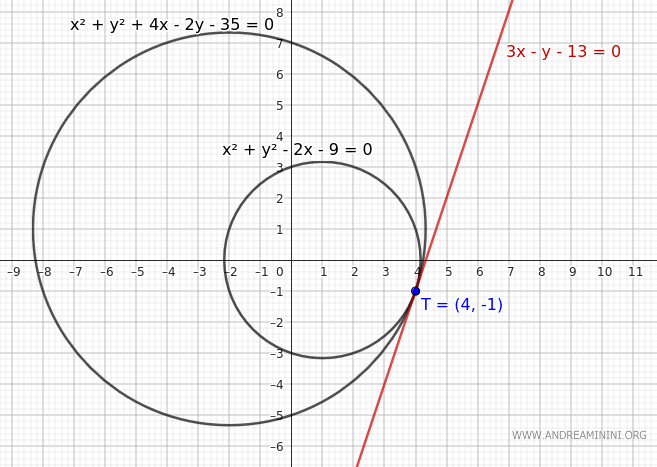
$$ 3x -y - 13 = 0 $$

Quest'ultima è l'equazione della retta tangente passante per il punto $ T(4, -1) $

 

Soluzione alternativa

Considero le due circonferenze dell'esempio precedente

$$ x^2+y^2-2x-9=0 $$

$$ x^2+y^2+4x-2y-35=0 $$

In questo caso costruisco un sistema di equazioni con le due equazioni delle circonferenze:

$$ \begin{cases} x^2+y^2-2x-9=0 \\ \\ x^2+y^2+4x-2y-35=0 \end{cases} $$

Applico il metodo della riduzione e sottraggo la prima equazione dalla seconda (o viceversa).

$$ \begin{cases} x^2+y^2-2x-9=0 \\ \\ x^2+y^2+4x-2y-35 - (x^2+y^2-2x-9=0)=0 \end{cases} $$

$$ \begin{cases} x^2+y^2-2x-9=0 \\ \\ 6x-2y-26=0 \end{cases} $$

$$ \begin{cases} x^2+y^2-2x-9=0 \\ \\ 3x-y-13=0 \end{cases} $$

 

L'equazione 3x-y-13=0 è l'asse radiale che coincide con la retta tangente quando le due circonferenze sono secanti.

Quindi, il sistema iniziale è equivalente al sistema formato dall'equazione di una circonferenza e dall'equazione dell'asse radiale.

$$ \begin{cases} x^2+y^2-2x-9=0 \\ \\ y = 3x -13 \end{cases} $$

Sostituisco y nella prima equazione

$$ \begin{cases} x^2+(3x-13)^2-2x-9=0 \\ \\ y = 3x -13 \end{cases} $$

$$ \begin{cases} x^2+(3^2x^2-2 \cdot 3x \cdot 13+13^2)-2x-9=0 \\ \\ y = 3x -13=0 \end{cases} $$

$$ \begin{cases} x^2+(9x^2-78x+169)-2x-9=0 \\ \\ y = 3x -13 \end{cases} $$

$$ \begin{cases} 10x^2-80x+160=0 \\ \\ y = 3x -13 \end{cases} $$

$$ \begin{cases} x^2-8x+16=0 \\ \\ y = 3x -13=0 \end{cases} $$

A questo punto trovo le soluzioni dell'equazione di secondo grado.

$$ \Delta = b^2-4ac = (-8)^2-4 \cdot 16 = 64 - 64 = 0 $$

L'equazione di secondo grado ha una sola soluzione

$$ x = \frac{-b \pm \sqrt{ \Delta } }{2a} $$

$$ x = \frac{-(-8) \pm \sqrt{ 0 } }{2 \cdot 1} $$

$$ x = \frac{8}{2} $$

$$ x = 4 $$

Una volta trovata la coordinata x=4 la sostituisco nell'equazione della retta per trovare il valore corrispondente della y.

$$ y = 3x-13 $$

$$ y = 3 \cdot 4-13 $$

$$ y = 12-13 $$

$$ y = -1 $$

Pertanto, il punto di tangenza tra le due circonferenze si trova nel punto (x;y)=(4,-1)

$$ T(4,-1) $$

Ecco il grafico delle circonferenze e della retta tangente.

Teorema delle circonferenze tangenti

Dimostrazione

Considero due circonferenze tangenti, la prima con raggio r e la seconda con raggio r', ipotizzando che uno r>r' sia maggiore dell'altro.

Essendo circonferenze tangenti hanno un punto T in comune, ovvero il punto di tangenza.

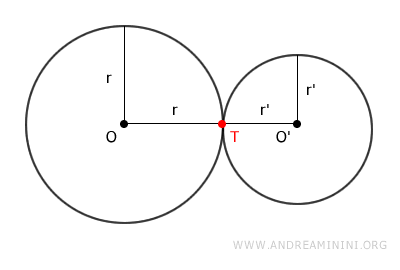
Il punto T è l'estremo del raggio di entrambe le circonferenze.

$$ r = OT $$

$$ r' = O'T $$

Nel punto di tangenza di una circonferenza passa una retta t perpendicolare al raggio.

Pertanto, nel punto T passa la stessa retta perpendicolare sia al raggio r che al raggio r'.

Di conseguenza, i punti O, T, O' sono tre punti allineati.

Essendo tre punti allineati, possono verificarsi due situazioni

• Se la distanza dai centri OO'=r+r' è uguale alla somma dei raggi, allora il centro di ciascuna circonferenza si trova all'esterno dell'altra e le due circonferenze sono tangenti esternamente
  
• Se la distanza dai centri OO'=r-r' è uguale alla differenza dei raggi, allora il centro di una circonferenza si trova all'interno dell'altra e le due circonferenze sono tangenti internamente
  

Osservazioni

Alcune osservazioni sulle circonferenze tangenti

• Quando due circonferenze sono tangenti, il punto di tangenza T appartiene al segmento OO' che congiunge i centri delle due circonferenze.
  

  Dimostrazione. Due circonferenze tangenti hanno un punto in comune T (il punto di tangenza). Nel punto di tangenza T passa una retta "t" perpendicolare al raggio. Poiché la retta perpendicolare a un segmento è una e una sola, deduco che la retta tangente "t" sia perpendicolare a entrambi i raggi OT e O'T delle due circonferenze. Di conseguenza, i centri delle due circonferenze O, O' e il punto di tangenza T sono tre punti allineati, ossia appartengono al segmento OO' e, quindi, alla stessa retta.

E così via.