Circonferenze esterne
Due circonferenze sono l'una esterna dell'altra se la distanza dei centri OO' è maggiore della somma dei raggi $$ \overline{OO'} > r+r' $$
Dove OO' è la distanza tra i centri delle due circonferenze mentre r e r' sono i raggi delle due circonferenze.
Dal punto di vista grafico, ogni circonferenza è esterna rispetto all'altra circonferenza.
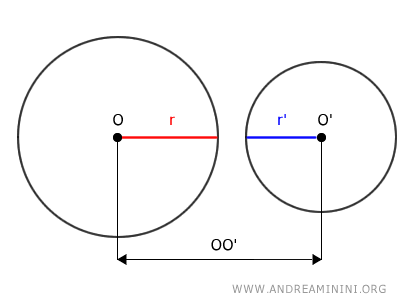
Se la distanza OO' è maggiore della somma dei raggi r+r', ogni centro O e O' è sicuramente un punto esterno dell'altra circonferenza.
Inoltre, la somma di ogni centro e il rispettivo raggio O+r e O'+r' non potrà mai intersecare l'altra circonferenza.
Un esempio pratico
Verifico se le due circonferenze definite dalle seguenti equazioni sono esterne:
$$ C_1 : x^2 + y^2 - 4x - 8y = -16 $$
$$ C_2 : x^2 + y^2 - 2x + 4y = 2 $$
Riscrivo le equazioni in forma standard $ (x-h)^2 + (y-k)^2 = r^2 $ per trovare il centro $ ( h,k) $ e il raggio $ r $ delle due circonferenze:
- Prima equazione: $$ x^2 + y^2 - 4x - 8y = -16 $$ Completo il quadrato per \(x\) e \(y\) aggiungendo e sottraendo i termini necessari: $$ (x^2 - 4x + 4) + (y^2 - 8y + 16) = -16 + 4 + 16 $$ $$ (x - 2)^2 + (y - 4)^2 = 4 $$ Quindi, la prima circonferenza ha centro \((2, 4)\) e raggio \(r_1 = \sqrt{4} = 2\).
- Seconda equazione: $$ x^2 + y^2 - 2x + 4y = 2 $$ Completo il quadrato per \(x\) e \(y\): $$ (x^2 - 2x + 1) + (y^2 + 4y + 4) = 2 + 1 + 4 $$ $$ (x - 1)^2 + (y + 2)^2 = 7 $$ Quindi, la seconda circonferenza ha centro \((1, -2)\) e raggio \(r_2 = \sqrt{7} \approx 2.65\).
A questo punto, calcolo la distanza tra i centri delle circonferenze utilizzando la formula della distanza euclidea tra due punti del piano.
$$ d = \sqrt{(x_2-x_1)^2+(y_2-y_1)^2 } $$
Il centro della prima circonferenza è \(O_1=(2, 4)\) quindi x1=2 e y1=4, mentre il centro della seconda circonferenza è \(O_2=(1, -2)\) quindi x2=1 e y2=-2
$$ d = \sqrt{(1 - 2)^2 + (-2 -4)^2} $$
$$ d = \sqrt{(-1)^2 + (-6)^2} $$
$$ d= \sqrt{1 + 36} $$
$$ d = \sqrt{37} \approx 6.08 $$
Infine, verifico la condizione delle circonferenze esterne
Le circonferenze sono esterne se la distanza tra i centri è maggiore della somma dei raggi:
$$ d > r_1 + r_2 $$
$$ 6.08 > 2 + 2.65 $$
$$ 6.08 > 4.65 $$
Poiché \( 6.08 > 4.65 \), le due circonferenze sono esterne l'una all'altra.
Soluzione alternativa
Devo verificare se le due circonferenze sono esterne:
$$ C_1 : x^2 + y^2 - 4x - 8y = -16 $$
$$ C_2 : x^2 + y^2 - 2x + 4y = 2 $$
Utilizzo questa formula per trovare il centro delle circonferenze $ ( - \frac{a}{2} , - \frac{b}{2} ) $ considerando l'equazione della circonferenza nella forma $ x^2+y^2+ax+bx+c = 0 $
$$ C_1 : x^2 + y^2 - 4x - 8y + 16 = 0 $$
$$ C_2 : x^2 + y^2 - 2x + 4y - 2 = 0 $$
Nella prima circonferenza i coefficienti sono a=-4 e b=-8.
$$ O_1 = ( - \frac{a}{2} , - \frac{b}{2} ) = ( - \frac{-4}{2} , - \frac{-8}{2} ) = (2,4) $$
Nella seconda circonferenza i coefficienti sono a=-2 e b=4.
$$ O_2 = ( - \frac{a}{2} , - \frac{b}{2} ) = ( - \frac{-2}{2} , - \frac{4}{2} ) = (1,-2) $$
Utilizzo quest'altra formula per trovare i raggi delle circonferenze $ r = \sqrt{ ( - \frac{a}{2} )^2+ ( - \frac{b}{2} )^2 - c } $
Nella prima circonferenza a=-4, b=-8, c=16
$$ r_1 = \sqrt{ ( - \frac{a}{2} )^2+ ( - \frac{b}{2} )^2 - c } $$
$$ r_1 = \sqrt{ 2^2+4^2 - 16 } $$
$$ r_1 = \sqrt{ 4 +16 - 16 } $$
$$ r_1 = \sqrt{ 4} $$
$$ r_1 = 2 $$
Nella seconda circonferenza a=-2, b=4, c=-2
$$ r_2 = \sqrt{ ( - \frac{a}{2} )^2+ ( - \frac{b}{2} )^2 - c } $$
$$ r_2 = \sqrt{ 1^2+(-2)^2 - (-2) } $$
$$ r_2 = \sqrt{ 1 +4 + 2} $$
$$ r_2 = \sqrt{ 7 } $$
$$ r_2 \approx 2.65 $$
A questo punto calcolo la distanza euclidea tra i centri delle due circonferenze.
$$ d = \sqrt{(x_2-x_1)^2+(y_2-y_1)^2 } $$
Il centro della prima circonferenza è \(O_1=(2, 4)\) quindi x1=2 e y1=4, mentre il centro della seconda circonferenza è \(O_2=(1, -2)\) quindi x2=1 e y2=-2
$$ d = \sqrt{(1 - 2)^2 + (-2 - 4)^2} $$
$$ d = \sqrt{(-1)^2 + (-6)^2} $$
$$ d = \sqrt{1 + 36} $$
$$ d = \sqrt{37} \approx 6.08 $$
Poi verifico se è soddisfatta la condizione per le circonferenze esterne.
Due circonferenze sono esterne se la distanza tra i loro centri è maggiore della somma dei loro raggi:
$$ d > r_1 + r_2 $$
$$ 6.08 > 2 + 2.65 $$
$$ 6.08 > 4.65 $$
Poiché \( 6.08 > 4.65 \), deduco che le due circonferenze sono esterne.
E così via
