Formule di sdoppiamento nell'equazione della polare

Le formule di sdoppiamento consentono di esprimere le coordinate del punto e i parametri della curva in modo tale da ottenere l'equazione della polare.

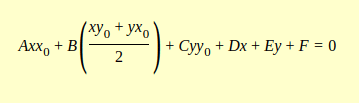
Per una curva conica rappresentata in coordinate cartesiane dall'equazione generale:

$$ Ax^2 + Bxy + Cy^2 + Dx + Ey + F = 0 $$

e un punto \( P(x_0, y_0) \), l'equazione della polare di \( P \) rispetto a questa conica è data da:

$$ Axx_0 + B\left(\frac{xy_0 + yx_0}{2}\right) + Cyy_0 + Dx + Ey + F = 0 $$

Ovviamente parliamo di curve coniche, come circonferenze, ellissi, parabole e iperboli, e di un punto esterno a queste curve.

Il caso più semplice è quello di una circonferenza $ x^2+y^2+ax+by+c=0 $

Il concetto di polare fu introdotto durante lo sviluppo della geometria analitica e proiettiva nel XIX secolo. Matematici come Poncelet e Chasles hanno contribuito significativamente allo sviluppo di queste teorie.

Se ho una curva conica come una circonferenza e prendo un punto P esterno alla conica, posso definire una retta chiamata "retta polare" del punto P rispetto alla conica.

La retta polare è quella retta (rossa) che taglia la circonferenza nei punti di tangenza A e B che appartengono alle rette tangenti che passano per il punto esterno P.

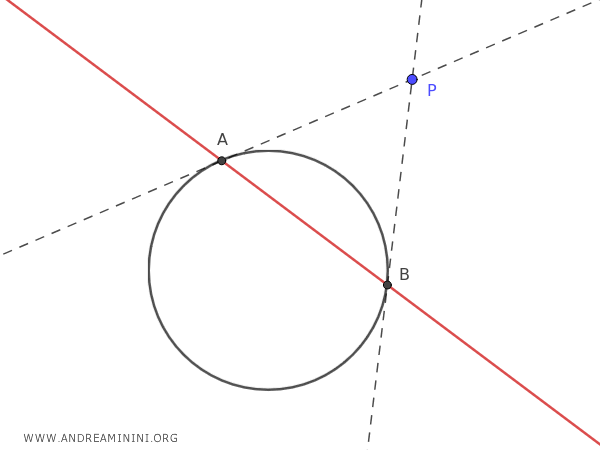
In altre parole, la retta polare è una retta tale i cui punti di intersezione A e B sulla circonferenza coincidono con i punti di tangenza delle rette tangenti che passano per il punto esterno P.

Nel caso particolare in cui il punto P si trova sulla circonferenza, il risultato coincide con la retta tangente.

Quindi, in questo caso ottengo l'equazione della retta tangente.

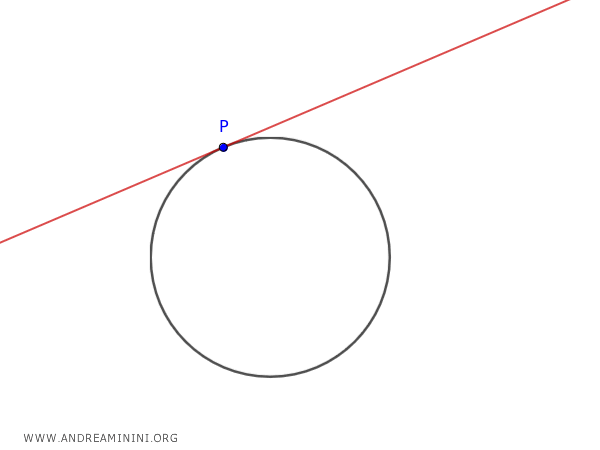
Pertanto, le "formule di sdoppiamento" sono equazioni che mi permettono di trovare l'equazione della tangente o della polare in un punto P della conica.

Nota. Il termine "sdoppiamento" si riferisce al fatto che, considerando un punto sulla conica, posso pensare a questo punto come risultato della coesistenza di due punti di intersezione infinitamente vicini (quasi coincidenti) sulla conica, da cui la tangente tocca la conica in quel punto specifico.

Utilizzando la forma implicita della conica posso derivare le seguenti espressioni:

Rappresentazione simmetrica:

$$ Axx_0 + B\left(\frac{xy_0 + yx_0}{2}\right) + Cyy_0 + Dx + Ey = 0 $$

Formule di sdoppiamento per coniche:

Per una circonferenza \( x^2 + y^2 + 2gx + 2fy + c = 0 \):

$$ xx_0 + yy_0 + g(x + x_0) + f(y + y_0) + c = 0 $$

Per una parabola \( y^2 = 4ax \):

$$ yy_0 = 2a(x + x_0) $$

A cosa servono? Le formule di sdoppiamento sono utilizzate per trovare le equazioni delle tangenti, normali e polari relative a curve algebriche. Ad esempio, posso usare la formula di sdoppiamento su una circonferenza per trovare l'equazione della retta tangente in un punto P della circonferenza. 

Esempio pratico

Faccio un esempio pratico per chiarire meglio il concetto delle formule di sdoppiamento e della polare.

Considero una circonferenza con centro nell'origine degli assi e raggio \( r = 5 \), quindi l'equazione è:

$$ x^2 + y^2 = 25 $$

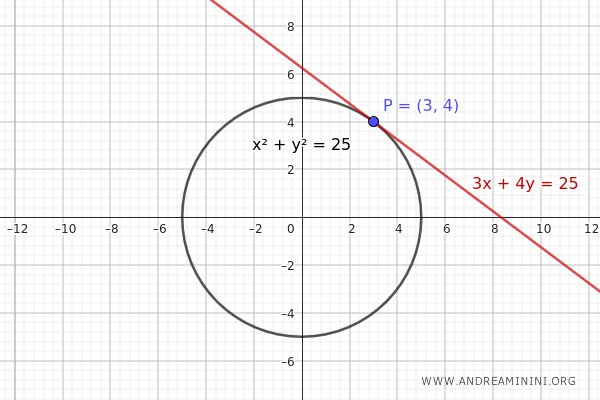
Prendo un punto sulla circonferenza \( P(3, 4) \).

Nota. Per verificare che si tratti di un punto sulla circonferenza basta sostituire le coordinate del punto x=3 e y=4 nell'equazione della circonferenza $$ x^2 + y^2 = 25 $$ $$  3^2 + 4^2 = 25 $$ $$ 9+16 =25 $$ $$ 25=25 $$ L'identità è confermata.

Utilizzo la formula \( xx_0 + yy_0 = r^2 \) per trovare l'equazione della tangente nel punto \( P(3, 4) \).

Sostituisco \( x_0 = 3 \), \( y_0 = 4 \), e \( r^2 = 25 \) nella formula:

$$ x \cdot 3 + y \cdot 4 = 25 $$

$$ 3x + 4y = 25 $$

Questa è l'equazione della retta tangente alla circonferenza nel punto \( P(3, 4) \).

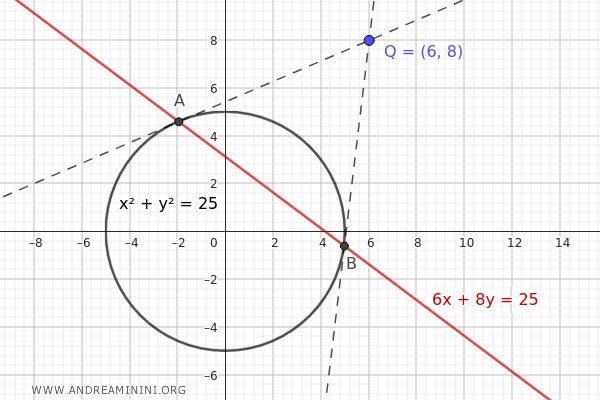
A questo punto trovo l'equazione della retta polare rispetto a un punto \( Q \) esterno alla circonferenza \( x^2 + y^2 = 25 \), ad esempio \( Q(6, 8) \).

La polare del punto \( Q \) rispetto alla circonferenza \( x^2 + y^2 = 25 \) è la retta che rappresenta tutti i punti di tangenza delle rette tangenti che passano per il punto \( Q \).

Usiamo la formula:

$$ xx_0 + yy_0 = r^2 $$

Ma in questo caso, \( (x_0, y_0) \) è il punto \( Q(6, 8) \), e la retta polare sarà:

$$ x \cdot 6 + y \cdot 8 = 25 $$

$$ 6x + 8y = 25 $$

Questa retta rappresenta la polare del punto \( Q(6, 8) \) rispetto alla circonferenza \( x^2 + y^2 = 25 \).

I punti di intersezione della retta polare coincidono con i punti di tangenza A e B sulla circonferenza delle due rette tangenti che passano anche per il punto esterno \( Q(6, 8) \).

In conclusione, in questo esempio pratico ho utilizzato la formula di sdoppiamento per trovare l'equazione della tangente a una circonferenza e per determinare la polare di un punto esterno alla circonferenza.

Osservazioni

Alcuni osservazioni e note a margine sulle formule di sdoppiamento

• La polare di un punto rispetto a una conica può essere vista come l'insieme dei punti di tangenza delle tangenti alla conica passanti per quel punto.
• Se \( P \) è un punto esterno a una conica, la sua polare rispetto a quella conica sarà la retta tangente alla conica nei punti di contatto delle tangenti da \( P \).
• Se il punto \( P \) giace sulla polare di un punto \( Q \), allora \( Q \) giace sulla polare di \( P \).

E così via.