Retta tangente, secante o esterna alla circonferenza
Una retta è tangente a una circonferenza quando hanno un solo punto in comune, è esterna se non hanno punti in comune, è secante se hanno due punti in comune.

Come verificare se una retta è tangente, secante o esterna a una circonferenza
Per conoscere se una retta è tangente, esterna o secante in geometria analitica, devo conoscere il raggio r e il centro della circonferenza C(x0;y0), l'equazione della retta y = mx+q.
Quando la circonferenza è tangente alla retta, la distanza tra la retta e la circonferenza è uguale al raggio.
La formula per la distanza da un punto \((x_0, y_0)\) alla retta \( y = mx + q \) è data da:
$$ d = \frac{|mx_0 - y_0 + q|}{\sqrt{m^2 + 1}} $$
Dal confronto tra il raggio e la distanza possono nascere tre situazioni
- Se r=d il raggio è uguale alla distanza, quindi la circonferenza e la retta sono tangenti.
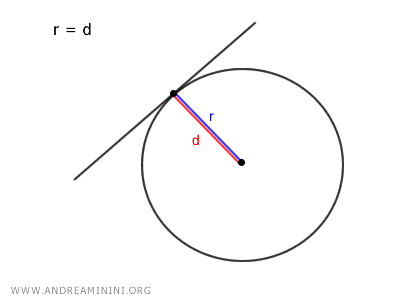
- Se r<d il raggio è inferiore alla distanza, quindi la retta è esterna alla circonferenza
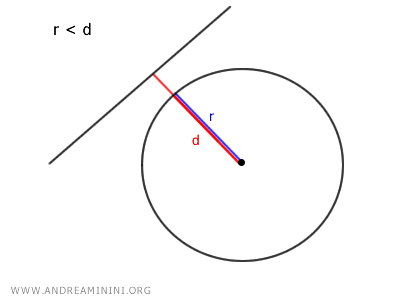
- Se r>d il raggio è maggiore della distanza, quindi la retta è una secante e interseca la circonferenza in due punti distinti.
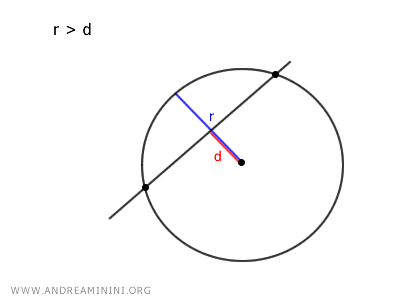
Un esempio pratico
In questo esempio considero l'equazione della retta:
$$ y = 2x + 3 $$
La circonferenz ha il centro nel punto \( C(1, 4) \) e il raggio pari a:
$$ r = \frac{1}{\sqrt{5}} $$
Per verificare se la retta è tangente, secante o esterna alla circonferenza, calcolo la distanza euclidea tra la retta e il centro della circonferenza.
La formula per la distanza \( d \) da un punto \((x_0, y_0)\) alla retta \( y = mx + q \) è:
$$ d = \frac{|mx_0 - y_0 + q|}{\sqrt{m^2 + 1}} $$
In questo caso l'equazione della retta è y=2x+3 quindi m=2 e q=3
$$ d = \frac{|2x_0 - y_0 + 3|}{\sqrt{2^2 + 1}} $$
$$ d = \frac{|2x_0 - y_0 + 3|}{\sqrt{4 + 1}} $$
Il centro del cerchio è C(1,4) quindi x0=1 e y0=4
$$ d = \frac{|2 \cdot 1 - 4 + 3|}{\sqrt{4 + 1}} $$
$$ d = \frac{|2 - 1|}{\sqrt{5}} $$
$$ d = \frac{|1|}{\sqrt{5}} $$
$$ d = \frac{1}{\sqrt{5}} $$
Il raggio della circonferenza e la distanza sono uguali, pertanto la retta è tangente alla circonferenza.
$$ r = d = \frac{1}{\sqrt{5}} $$
Ecco la rappresentazione grafica del problema
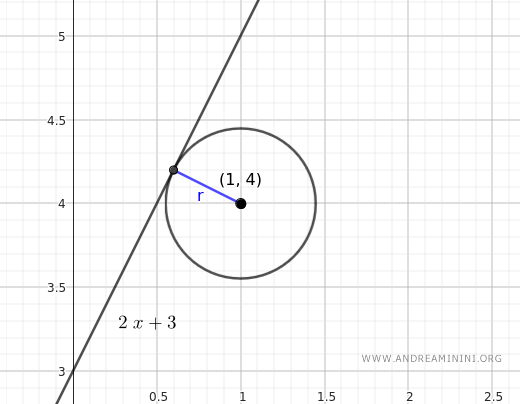
E così via.
