Teorema degli archi congruenti in una circonferenza e dei poligoni regolari
In una circonferenza divisa in tre o più archi congruenti posso disegnare un poligono regolare inscritto congiungendo gli estremi di ogni arco contiguo e un poligono regolare circoscritto congiungendo le tangenti alla circonferenza.
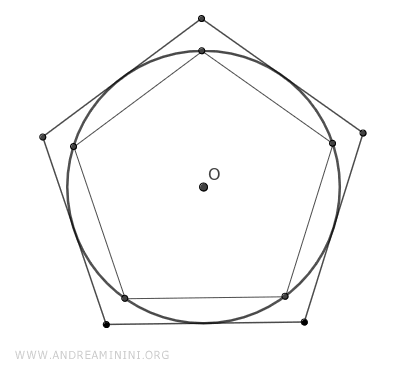
Vale anche il teorema inverso.
Quando inserisco un poligono regolare con n angoli dentro una circonferenza (inscrizione) o posiziono un poligono regolare in modo che ogni suo lato tocchi la circonferenza (circoscrizione), ottengo una suddivisione della circonferenza stessa in n archi congruenti.
Un esempio pratico
A] Poligoni regolari inscritti
Prendo una circonferenza e individuo quattro punti sulla circonferenza in modo che siano equidistanti l'uno dall'altro.
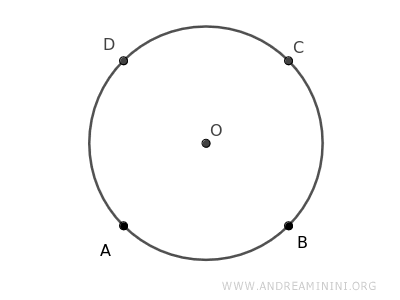
In questo modo divido la circonferenza in quattro archi congruenti (archi di uguale lunghezza).
$$ \overparen{AB} \cong \overparen{BC} \cong \overparen{CD} \cong \overparen{AD} $$
Ora, congiungo ciascuno di questi punti selezionati con i suoi adiacenti tramite dei segmenti.
I punti diventano i vertici di un poligono inscritto nella circonferenza. In questo caso è un quadrato.
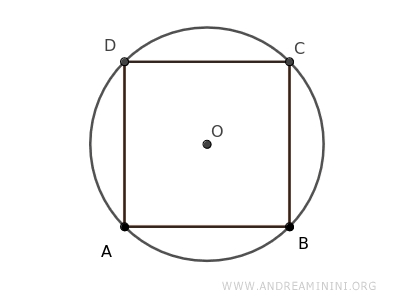
Ogni angolo interno del quadrato tocca la circonferenza, e ogni lato del quadrato è una corda della circonferenza.
Teorema inverso
Considero una figura perfettamente simmetrica, come un quadrato o un triangolo equilatero.
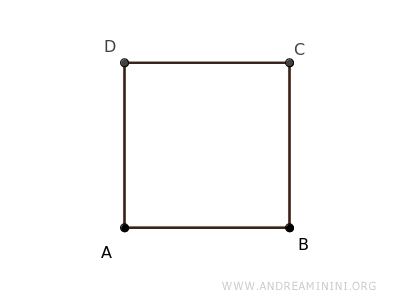
Individuo il centro (O) del poligono regolare, ossia il punto equidistante (d) dai vertici del poligono che si trova nel punto di intersezione delle bisettrici.
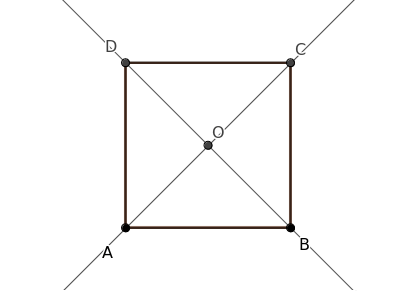
Disegno una circonferenza con centro O e raggio pari alla distanza d.
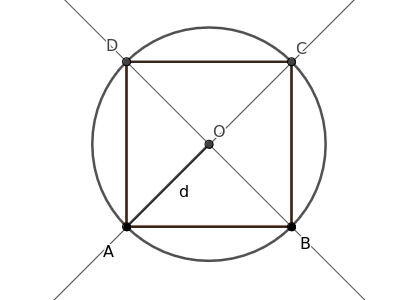
Ogni vertice del poligono regolare tocca la circonferenza in un punto, e questi punti di contatto dividono la circonferenza in sezioni uguali o archi congruenti.
Ad esempio, se il poligono regolare ha 5 lati (pentagono regolare), la circonferenza viene suddivisa in 5 archi uguali.
B] Poligoni regolari circoscritti
Prendo una circonferenza e la suddivido in n=4 archi congruenti.

Disegno le rette tangenti agli estremi degli archi AB, BC, CD, AD.
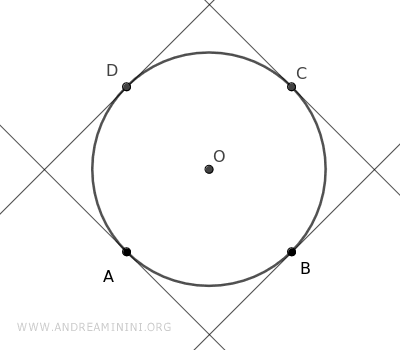
Le quattro rette tangenti si intersecano in quattro punti esterni alla circonferenza E, F, G, H.
Congiungendo questi punti ottengo un poligono regolare circoscritto. In questo caso un quadrato.
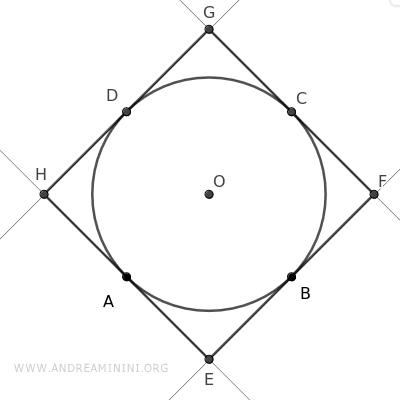
I lati del quadrato toccano la circonferenza in un solo punto per lato, circoscrivendo la circonferenza.
Teorema inverso
A questo punto disegno un poligono regolare, un quadrato.
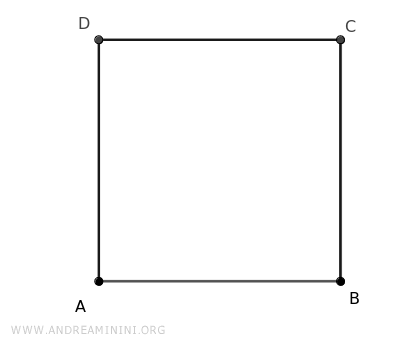
Traccio le bisettrici di ogni angolo e individuo il centro (O) del poligono regolare.
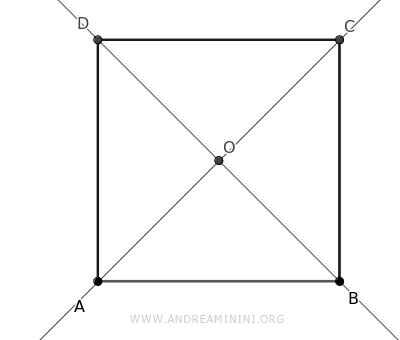
A questo punto traccio una circonferenza che tocca i lati del poligono senza tagliarli.
Il punto di contatto tra ciascun lato del poligono e la circonferenza è il punto di tangenza.
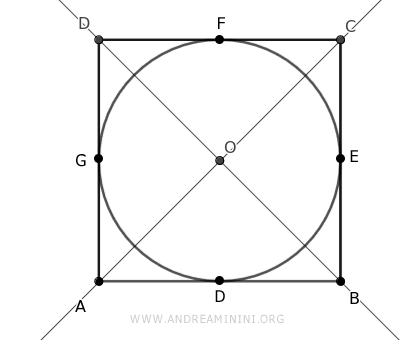
I punti di tangenza dividono la circonferenza in quattro archi uguali (congruenti).
E così via.
