Asse centrale del fascio di circonferenze
L'asse centrale del fascio di circonferenze è una retta che rappresenta il luogo geometrico dei centri di tutte le circonferenze appartenenti al fascio.

In altre parole, è la linea lungo la quale si trovano i centri di tutte le circonferenze che possono essere generate a partire da una particolare famiglia di circonferenze.
Un fascio di circonferenze è l'insieme di tutte le circonferenze che possono essere descritte dall'equazione generale:
$$ C_1 + \lambda C_2 = 0 $$
Dove \(C_1\) e \(C_2\) sono due circonferenze generatrici del fascio e \(\lambda\) è un parametro reale.
L'asse centrale di questo fascio è la retta che passa attraverso i centri delle due circonferenze \(C_1\) e \(C_2\) ed è perpendicolare all'asse radicale.
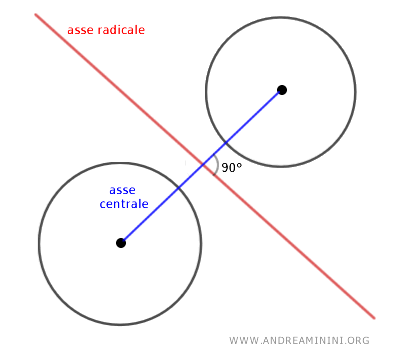
Ogni circonferenza generata nel fascio avrà il suo centro sull'asse centrale.
Quindi, si può immaginare come una sorta di "via dei centri" delle circonferenze del fascio.

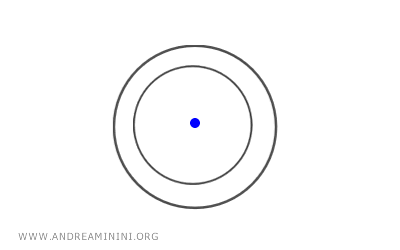
Se le circonferenze generatrici \(C_1\) e \(C_2\) sono concentriche (hanno lo stesso centro), l'asse centrale del fascio di circonferenze si riduce a un singolo punto, il centro comune delle circonferenze.
Nota. L'idea dell'asse centrale può essere estesa a più dimensioni, come ad esempio nell'analisi dei fasci di sfere in geometria tridimensionale. In questo caso, l'asse centrale diventerebbe un piano lungo il quale giacciono i centri di tutte le sfere del fascio.
Un esempio pratico
Considero di avere due circonferenze generatrici con le seguenti equazioni:
$$ C_1: (x - 1)^2 + (y - 2)^2 - 4 = 0 $$
$$ C_2: (x - 3)^2 + (y - 4)^2 - 9 = 0 $$
I centri delle circonferenze \(C_1\) e \(C_2\) sono rispettivamente \( A= (1, 2) \) e \( B= (3, 4) \).
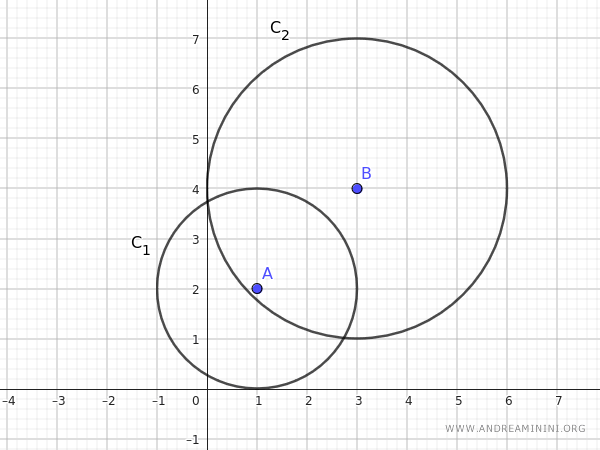
L'asse centrale del fascio è la retta che passa attraverso questi due punti. L'equazione della retta può essere trovata usando la formula della retta passante per due punti:
$$ \frac{y - y_1}{y_2 - y_1} = \frac{x - x_1}{x_2 - x_1} $$
Sostituendo i valori dei centri delle circonferenze:
$$ \frac{y - 2}{4 - 2} = \frac{x - 1}{3 - 1} $$
$$ \frac{y - 2}{2} = \frac{x - 1}{2} $$
Moltiplicando entrambi i membri per 2, ottengo:
$$ y - 2 = x - 1 \implies y = x + 1 $$
Quindi, l'asse centrale del fascio di queste circonferenze è la retta \( y = x + 1 \).
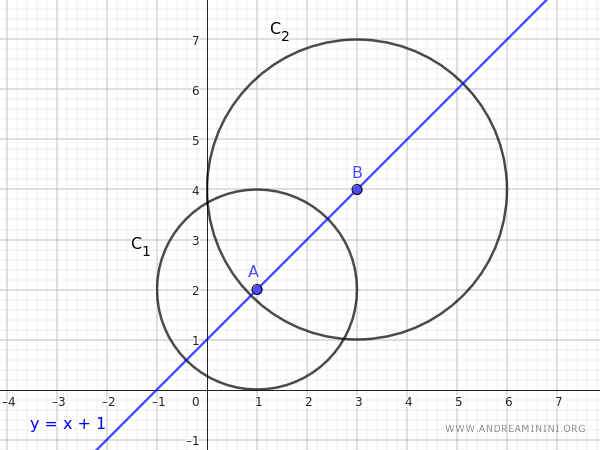
L'asse centrale del fascio di circonferenze è la retta che contiene i centri delle circonferenze del fascio.
Costruisco il fascio di rette delle due circonferenze.
$$ C_1 + \lambda C_2 = 0 $$
$$ [ (x - 1)^2 + (y - 2)^2 - 4 ] + \lambda \cdot [ (x - 3)^2 + (y - 4)^2 - 9 ] = 0 $$
Genero una circonferenza del fascio usando il valore $ \lambda = 2 $
$$ [ (x - 1)^2 + (y - 2)^2 - 4 ] + 2 \cdot [ (x - 3)^2 + (y - 4)^2 - 9 ] = 0 $$
$$ [ x^2-2x+1 + y^2-4y+4 - 4 ] + 2 \cdot [ x^2 - 6x+ 9 + y^2-8y +16 - 9 ] = 0 $$
$$ x^2-2x+1 + y^2-4y + 2x^2 - 12x + 2y^2 -16y+32= 0 $$
$$ 3x^2 + 3y^2 -14x -20y+33= 0 $$
Divido tutto per tre
$$ x^2 + y^2 - \frac{14}{3}x - \frac{20}{3}y+11= 0 $$
Questa circonferenza appartiene al fascio di rette e ha il centro nel punto
$$ ( -\frac{a}{2} , -\frac{b}{2} ) $$
$$ ( -\frac{-\frac{14}{3}}{2} , -\frac{-\frac{20}{3}}{2} ) $$
$$ ( \frac{14}{6} , \frac{20}{6} ) $$
$$ ( \frac{7}{3} , \frac{10}{3} ) $$
Il centro (7/3,10/3) della circonferenza generata appartiene all'asse centrale del fascio di circonferenze.
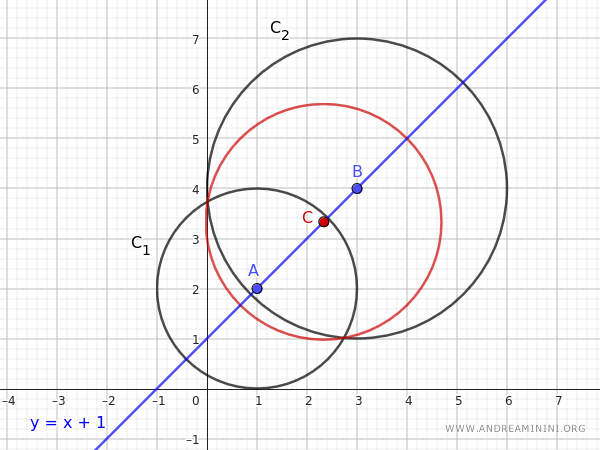
Lo stesso accade per tutte le altre circonferenze generate dal fascio di circonferenze.
E così via.
