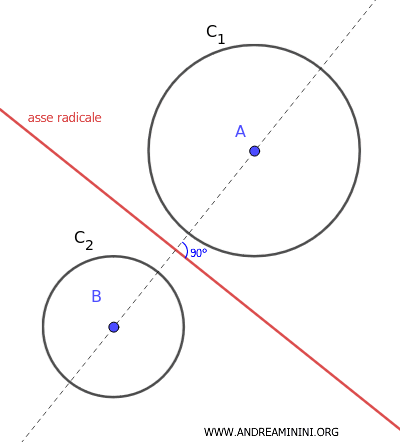
Asse radicale
L'asse radicale di due circonferenze non concentriche è il luogo geometrico dei punti che hanno la stessa potenza rispetto a entrambi i cerchi.
La potenza di un punto \( P \) con coordinate \((x_0, y_0)\) rispetto a una circonferenza con centro \((h, k)\) e raggio \( r \) è data dal quadrato della distanza del punto dal centro del cerchio meno il quadrato del raggio del cerchio.
$$ \text{Potenza} = d^2 - r^2 $$
Dove \( d \) è la distanza del punto \( P \) dal centro del cerchio, mentre \( r \) è il raggio del cerchio.
La distanza tra due punti \( P \) e il centro del cerchio \( (h, k) \) è espressa dalla formula:
$$ d = \sqrt{(x_0 - h)^2 + (y_0 - k)^2} $$
Quindi, la potenza del punto \( P \) rispetto a una circonferenza è:
$$ \text{Potenza} = (x_0 - h)^2 + (y_0 - k)^2 - r^2 $$
L'asse radicale è quindi il luogo dei punti per cui la differenza delle potenze rispetto ai due cerchi è zero, cioè:
$$ (x_0 - h_1)^2 + (y_0 - k_1)^2 - r_1^2 = (x_0 - h_2)^2 + (y_0 - k_2)^2 - r_2^2$$
Se le circonferenze hanno le equazioni in forma generale, per trovare l'asse radicale posso sottrarre l'una dall'altra. $$ x^2-y^2+ ax+by+c = x^2-y^2+a'x + b'y + c' $$ $$ \require{cancel} \cancel{x^2}-\cancel{y^2}+ ax+by+c = \cancel{x^2}- \cancel{y^2}+a'x + b'y + c' $$ $$ ax+by+c -a'x - b'y - c' = 0 $$ $$ (a-a')x+(b-b')y+c - c' = 0 $$ In questo modo ottengo un'equazione lineare dove x e y sono le coordinate dei punti dell'asse radiale. Ricavo la variabile y $$ y = - \frac{a-a'}{b-b'} x - (c-c') $$ In questo modo ottengo il coefficiente angolare dell'asse radiale $$ m = - \frac{a-a'}{b-b'} $$
L'asse radicale si presenta come una retta perpendicolare alla linea che unisce i centri delle due circonferenze.
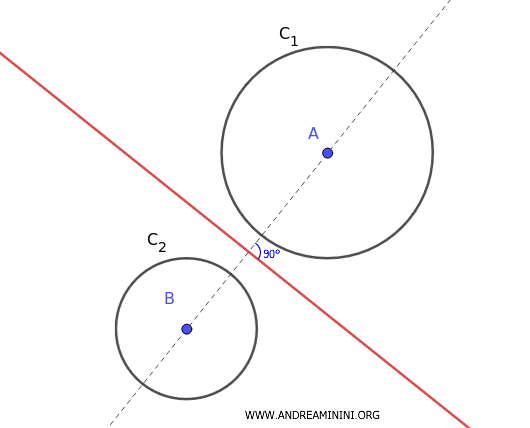
Per ogni punto P sull'asse radicale, le lunghezze dei segmenti tangenti tracciati verso le due circonferenze sono uguali. Ad esempio PC≅PF
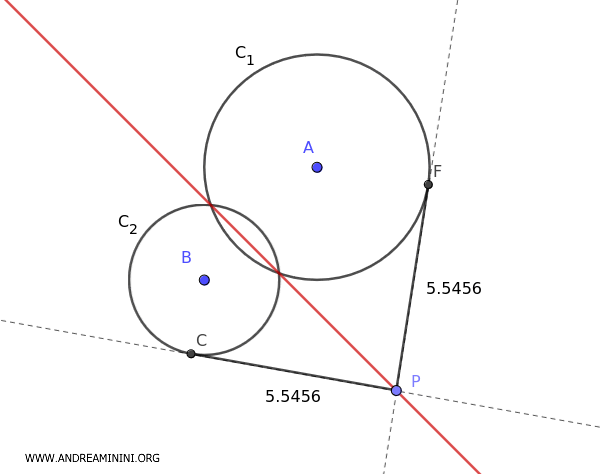
Se le due circonferenze sono secanti, la retta radicale passa per i due punti di intersezione.
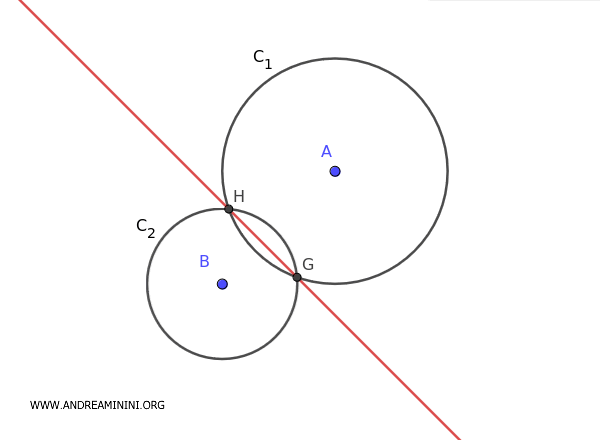
Se le due circonferenze sono tangenti, la retta radicale passa per il punto di tangenza.
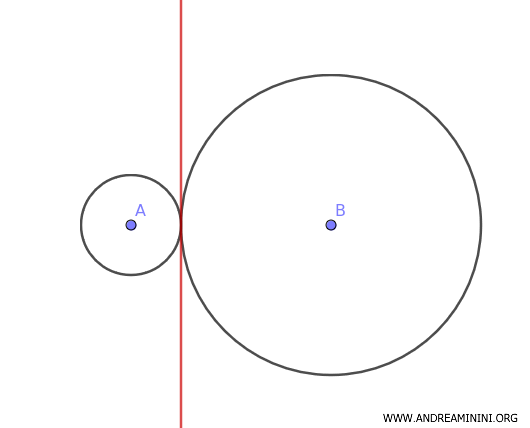
Un esempio pratico
Considero due circonferenze con le seguenti equazioni in forma standard:
$$ C_1 : \ (x - 4)^2 + (y - 4)^2 = 9 $$
$$ C_2 : \ (x - 1)^2 + (y - 1)^2 = 4 $$
La prima circonferenza ha il centro nel punto (4,4) e il raggio uguale a 3 poiché r2=9 quindi r=3.
La seconda circonferenza ha il centro nel punto (1,1) e il raggio uguale a 2 poiché r2=4 quindi r=2.
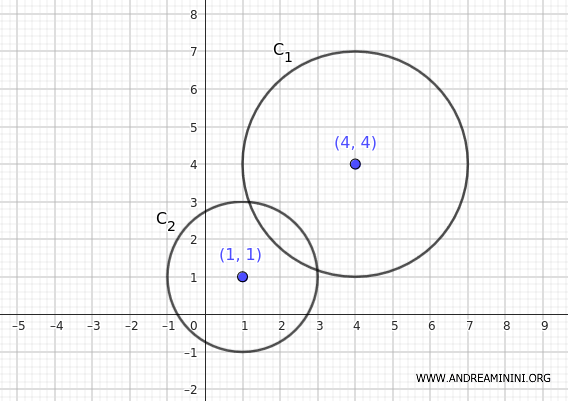
La potenza di un generico punto P(x,y) rispetto alla prima circonferenza che ha centro in (h,k)=(4,4) e raggio r=3 è la seguente:
$$ W_1 = (x - h)^2 + (y - k)^2 - r^2 $$
$$ W_1 = (x - 4)^2 + (y - 4)^2 - 3^2 $$
$$ W_1 = (x - 4)^2 + (y - 4)^2 - 9 $$
La potenza dello stesso punto P(x,y) rispetto alla seconda circonferenza che ha il centro in (h,k)=(1,1) e raggio r=2 è:
$$ W_2 = (x - h)^2 + (y - k)^2 - r^2 $$
$$ W_2 = (x - 1)^2 + (y - 1)^2 - 2^2 $$
$$ W_2 = (x - 1)^2 + (y - 1)^2 - 4 $$
Per ottenere il loro asse radicale eguaglio le potenze
$$ W_1 = W_2 $$
$$ (x - 4)^2 + (y - 4)^2 - 9 = (x - 1)^2 + (y - 1)^2 - 4 $$
Semplifico questa equazione e ottengo la retta che rappresenta l'asse radicale.
$$ x^2-8x+16 + y^2-8x+16 - 9 = x^2 - 2x +1 + y^2-2y+1 - 4 $$
$$ -8x -8y+23 = - 2x -2y - 2 $$
$$ -2y+8y = -8x +23+2+2x $$
$$ 6y = -6x +25 $$
$$ y = \frac{-6x +25}{6} $$
$$ y = -x + \frac{25}{6} $$
Poiché le due circonferenze sono secanti, l'asse radicale è la retta che passa per i due punti di intersezione.
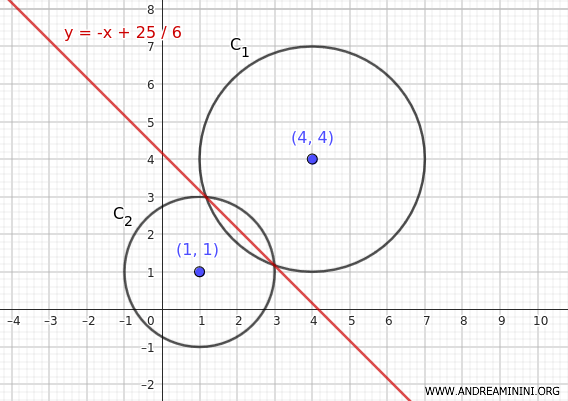
Esempio 2
Considero due circonferenze con le equazioni in forma generale
$$ C_1 : x^2+y^2-8x-8y+23 = 0 $$
$$ C_2 : x^2+y^2 - 2x-2y-2 = 0 $$
In questo caso non conosco il centro e i raggi, per ottenerli dovrei calcolarli.
Tuttavia, se il mio obiettivo è ricavare l'equazione dell'asse radicale, posso ottenerla semplicemente sottraendo un'equazione generale della circonferenza dall'altra.
$$ C_1 = C_2 $$
$$ x^2+y^2-8x-8y+23 = x^2+y^2 - 2x-2y-2 $$
$$ \require{cancel} \cancel{x^2}+ \cancel{y^2}-8x-8y+23 = \cancel{x^2}+ \cancel{y^2} - 2x-2y-2 $$
In questo modo ottengo un'equazione lineare:
$$ -8y+2y = 8x - 2x-2-23 $$
$$ -6y = 6x-25 $$
$$ 6y = -6x+25 $$
$$ y = \frac{ -6x+25}{6} $$
$$ y = -x + \frac{25}{6} $$
Ho così trovato l'equazione dell'asse radicale delle due circonferenze.

Esempio 2
In questo caso ho due circonferenze con le equazioni in forma generale
$$ C_1 : x^2+y^2-8x-8y+23 = 0 $$
$$ C_2 : x^2+y^2 - 2x-2y-2 = 0 $$
In questo caso non conosco il centro e i raggi, per ottenerli dovrei calcolarli.
Tuttavia, se il mio obiettivo è ricavare l'equazione dell'asse radicale, posso ottenerla semplicemente sottraendo un'equazione generale della circonferenza dall'altra.
$$ C_1 = C_2 $$
$$ x^2+y^2-8x-8y+23 = x^2+y^2 - 2x-2y-2 $$
$$ \require{cancel} \cancel{x^2}+ \cancel{y^2}-8x-8y+23 = \cancel{x^2}+ \cancel{y^2} - 2x-2y-2 $$
In questo modo ottengo un'equazione lineare:
$$ -8y+2y = 8x - 2x-2-23 $$
$$ -6y = 6x-25 $$
$$ 6y = -6x+25 $$
$$ y = \frac{ -6x+25}{6} $$
$$ y = -x + \frac{25}{6} $$
Ho così trovato l'equazione dell'asse radicale delle due circonferenze.

Esempio 3
Considero due circonferenze con le equazioni in forma generale:
$$ C_1 : x^2+y^2-2x=0 $$
$$ C_2 : x^2+y^2-10x+16=0 $$
Per ottenere l'equazione della retta tangente sottraggo la prima dalla seconda:
$$ x^2+y^2-2x = x^2+y^2-10x+16 $$
$$ \cancel{x^2}+\cancel{y^2}-2x = \cancel{x^2}+\cancel{y^2}-10x+16 $$
$$ -2x = -10x+16 $$
$$ -2x+10x = 16 $$
$$ 8x = 16 $$
$$ x = \frac{16}{8} $$
$$ x = 2 $$
In questo caso l'asse radicale è una retta parallela all'asse delle ordinate che passa per il punto x=2.
Poiché le due circonferenze sono tangenti, l'asse radicale passa esattamente nel punto di tangenza delle due circonferenze.
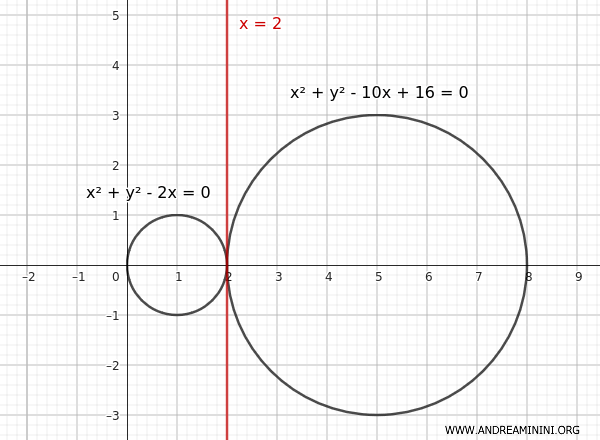
Esempio 4
Considero due circonferenze
$$ C_1 : (x-7)^2 + (y-7)^2= 9 $$
$$ C_2 : (x-3)^ + (y-2)^2=4 $$
La prima circonferenza ha il centro alle coordinate (h,k)=(7,7) e il raggio uguale uguale a $ r = \sqrt{9} = 3 $
La seconda circonferenza ha il centro alle coordinate (h,k)=(3,2) e il raggio uguale uguale a $ r = \sqrt{4} = 2 $
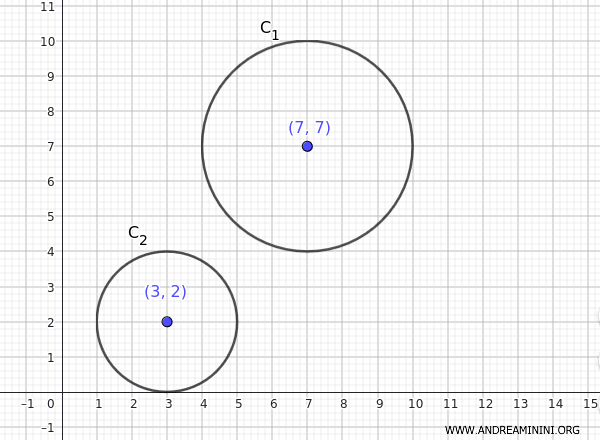
La potenza di un punto P(x,y) rispetto alla prima circonferenza che ha centro in (h,k)=(7,7) e raggio r=3 è:
$$ W_1 = (x - h)^2 + (y - k)^2 - r^2 $$
$$ W_1 = (x - 7)^2 + (y - 7)^2 - 3^2 $$
$$ W_1 = (x - 7)^2 + (y - 7)^2 - 9 $$
La potenza dello stesso punto P(x,y) rispetto alla seconda circonferenza che ha il centro in (h,k)=(3,2) e raggio r=2 è:
$$ W_2 = (x - h)^2 + (y - k)^2 - r^2 $$
$$ W_2 = (x - 3)^2 + (y - 2)^2 - 2^2 $$
$$ W_2 = (x - 3)^2 + (y - 2)^2 - 4 $$
Eguaglio le due potenze per ottenere l'asse radicale
$$ W_1 = W_2 $$
$$ (x - 7)^2 + (y - 7)^2 - 9 = (x - 3)^2 + (y - 2)^2 - 4 $$
Poi svolgo i calcoli algebrici necessari:
$$ x^2-14x+49 + y^2-14y+49 - 9 = x^2 - 6x +9 + y^2-4y+4 - 4 $$
$$ \require{cancel}{x^2}-14x+49 + \require{cancel}{y^2}-14x+49 - 9 = \require{cancel}{x^2} - 6x +9 + \require{cancel}{y^2}-4y+4 - 4 $$
$$ -14x -14y+98 - 9 = - 6x-4y+9 $$
$$ -14y+4y = - 6x+14x-89+9 $$
$$ -10y = 8x-80 $$
$$ 10y = -8x+80 $$
$$ y = \frac{-8x+80}{10} $$
$$ y = - \frac{8x}{10} + \frac{80}{10} $$
$$ y = - \frac{4x}{5} + 8 $$
Quest'ultima è l'equazione dell'asse radicale delle due circonferenze.
In questo caso le due circonferenze sono esterne, quindi l'asse radicale passa nello spazio esterno alle circonferenze.
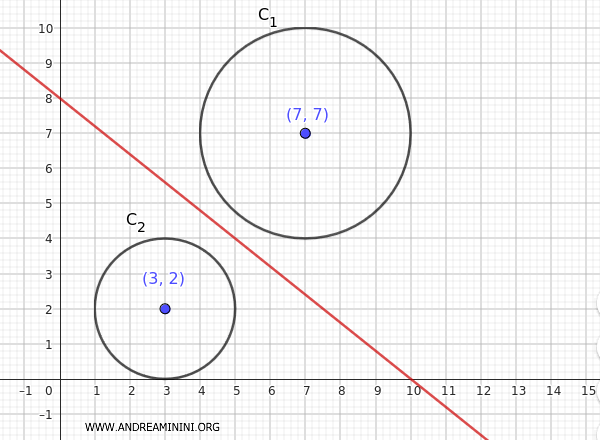
E così via.
