Principio di proporzionalità tra le circonferenze

Le lunghezze di due circonferenze sono proporzionali ai loro raggi. $$ c:c = r:r' $$

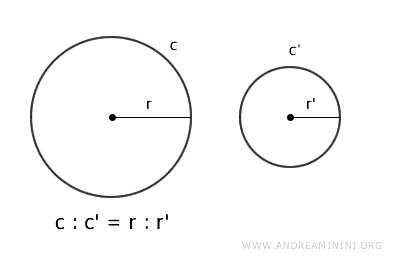
In altre parole, se prendo due circonferenze qualsiasi e le confronto, il rapporto tra le loro lunghezze è uguale al rapporto tra i loro raggi.

$$ \frac{c}{c'} = \frac{r}{r'} $$

Dove c e c' sono le lunghezze delle circonferenze mentre r e r' sono le misure dei raggi.

Nota. Da questo teorema si può deduce che esiste una relazione tra la circonferenza e il proprio raggio che va al di là della dimensione del cerchio. Quello che oggi chiamiamo "pi greco" ( π=3,1415... )  non è altro che il rapporto tra la circonferenza e il diametro (doppio del raggio).

La dimostrazione

Considero due circonferenze di lunghezza c e c' che hanno rispettivamente i raggi r e r'.

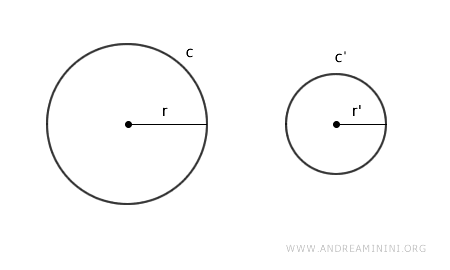
Disegno dei poligoni regolari iscritti nelle due circonferenze. Ad esempio degli esagoni.

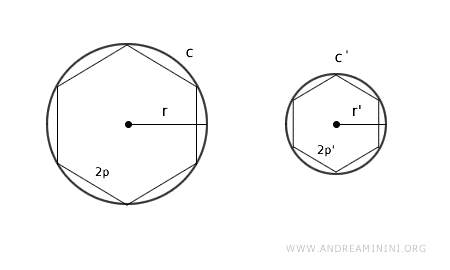
Essendo poligoni regolari, sono anche poligoni simili, quindi hanno il perimetro e tutti i lati proporzionali.

Inoltre, secondo un teorema dei poligoni regolari, anche i raggi delle circonferenze inscritte o circoscritte sono proporzionali.

Quindi, posso scrivere la seguente proporzione:

$$ 2p : 2p' = r: r' $$

Dove 2p è il perimetro e p è il semiperimetro del poligono regolare, mentre r è il raggio della circonferenza.

In altre parole, il rapporto di proporzionalità è lo stesso.

$$ k = \frac{2p}{2p'} = \frac{r}{r'} $$

Se ora traccio un poligono regolare circoscritto alla circonferenza, posso ripetere lo stesso ragionamento.

Ad esempio, considero sempre un esagono ma questa volta esterno alla circonferenza.

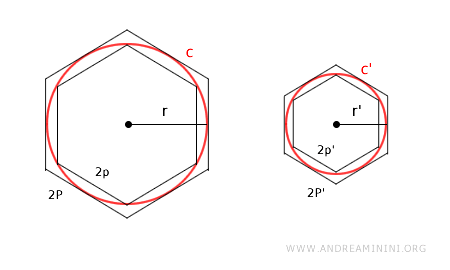
Anche in questo caso i poligoni sono regolari, quindi sono poligoni simili e hanno il perimetro, i lati e il raggio della circonferenza proporporzionali tra loro.

$$ 2P : 2P' = r: r' $$

Dove 2P è il perimetro e P è il semiperimetro del poligono regolare circoscritto, mentre r è il raggio della circonferenza.

Sapendo che il perimetro del poligono che circoscrive la circonferenza è sempre maggiore di quello inscritto, posso scrivere la seguente relazione:

$$ 2p < c < 2P $$

In altre parole, la lunghezza della circonferenza (c) è compresa tra il perimetro del poligono iscritto e quello del poligono circoscritto.

Moltiplico tutti i membri della relazione per k, ovvero per il rapporto di proporzionalità.

$$ 2p \cdot k < c \cdot k < 2P \cdot k $$

Sapendo che 2p'=2p·k e 2P'=2P·k posso scrivere anche

$$ 2p' < c' < 2P' $$

Quindi, esiste una relazione tra le lunghezze delle due circonferenze ed è pari al rapporto di proporzionalità dei poligoni regolari inscritti e circoscritti.

$$ c' = c \cdot k $$

ovvero

$$ k = \frac{c}{c'} $$

Sapendo che k è anche il rapporto di proporzionalità che c'è tra i raggi delle due circonferenze.

$$ k = \frac{c}{c'} = \frac{r}{r'} $$

Quindi, posso scrivere  la seguente proporzione:

$$ c : c' = r : r' $$

Questo dimostra la proporzionalità tra le lunghezze delle circonferenze e i rispettivi raggi.

Da quest'ultima posso dedurre anche la relazione tra le circonferenze e i diametri.

Sapendo che il diametro è il doppio del raggio, mi basta moltiplicare per due entrambi i raggi.

$$ c : c' = 2 \cdot r : 2 \cdot r' $$

$$ c : c' = d : d' $$

Poi permuto i medi della proporzione:

$$ c : d = c' : d' $$

In conclusione, il rapporto la la lunghezza della circonferenza (c) e il diametro (d) è costante indipendentemente dalle dimensioni della circonferenza stessa.

Questo valore costante è il numero che oggi conosciamo come "pi greco" ovvero 3,1415592...

E così via.