Il teorema delle corde proporzionali in una circonferenza
Quando due corde si intersecano all'interno di una circonferenza, i segmenti generati su ciascuna corda stabiliscono una proporzione tale che i segmenti di una corda sono i medi, mentre quelli sull'altra corda sono gli estremi della proporzione stessa.
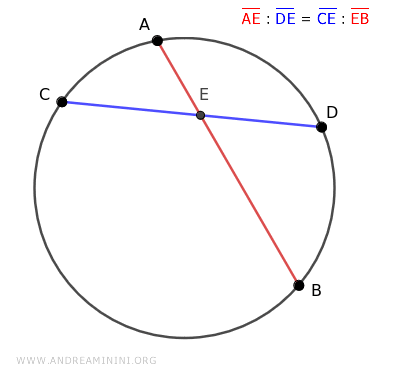
Non importa quale corda scelgo per rappresentare gli estremi e quale per i medi, la proporzione è comunque soddisfatta.
Si tratta di una similitudine tipica delle circonferenze.
Nota. In una proporzione i medi proporzionali sono i termini interni/centrali, mentre gli estremi proporzionali sono i termini esterni.
Un esempio pratico
Prendo come esempio una circonferenza con due corde AB e CD che si intersecano nel punto E all'interno della circonferenza.
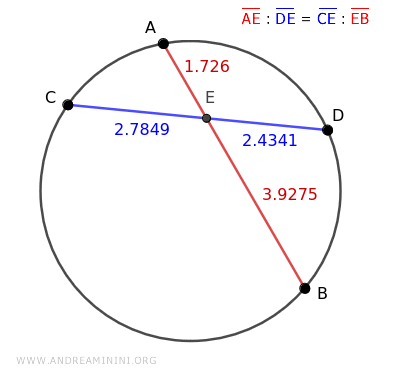
In base al teorema delle corde, i segmenti di una corda sono i medi proporzionali mentre quelli dell'altra corda sono gli estremi proporzionali.
$$ \overline{AE} : \overline{DE} = \overline{CE} : \overline{EB} $$
In questo caso i medi della proporzione sono i segmenti della corda blu CD, mentre gli estremi sono quelli della corda rossa AB.
Sostituisco le lunghezze dei segmenti.
$$ 1.726 : 2.4341 = 2.7849 : 3.9275 $$
Calcolo i due rapporti e ottengo lo stesso quoziente.
$$ 0.709 = 0.709 $$
La proporzione è soddisfatta.
Nota. Ovviamente, non cambierebbe nulla se invertissi la proporzione otterrei lo stesso risultato. Ad esempio prendessi come medi proporzionali i segmenti della corda rossa AB e come estremi proporzionali i segmenti della corda CD, la proporzione sarebbe comunque soddisfatta. $$ \overline{DE} : \overline{AE} = \overline{EB} : \overline{CE} $$ $$ 2.4341 : 1.726 = 3.9275 : 2.7849 $$ $$ 1.41 : 1.41 $$
La dimostrazione
Considero una circonferenza.
Traccio due corde AB e CD che si intersecano all'interno della circonferenza nel punto E.
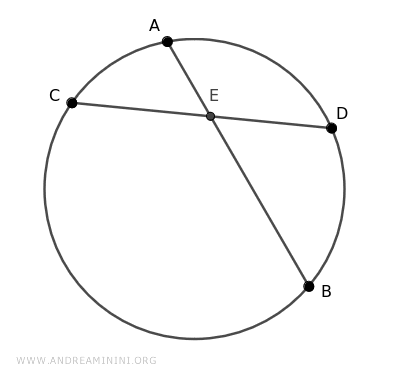
Aggiungo due segmenti AC e BD che congiungono gli estremi delle corde.
Si formano così due triangoli ACE e BDE.
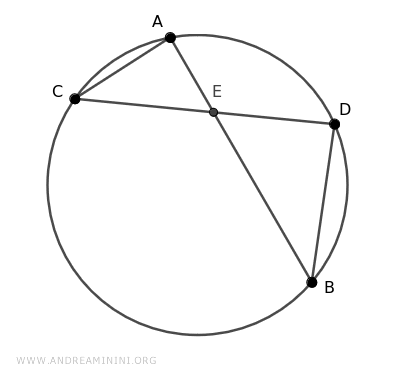
Questi due triangoli hanno un angolo congruente α≅α' al vertice E perché α e α' sono due angoli opposti al vertice.
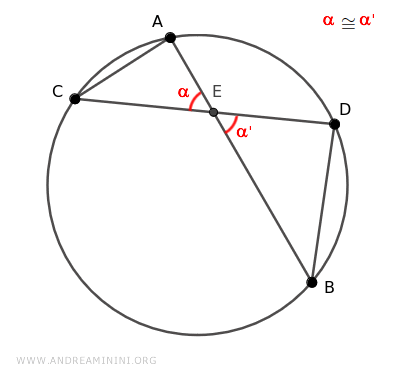
Hanno anche un altro angolo congruente β≅β', perché gli angoli β e β' sono angoli alla circonferenza che insistono sullo stesso arco di circonferenza AD.
Quindi, per il teorema degli angoli alla circonferenza sono angoli congruenti.
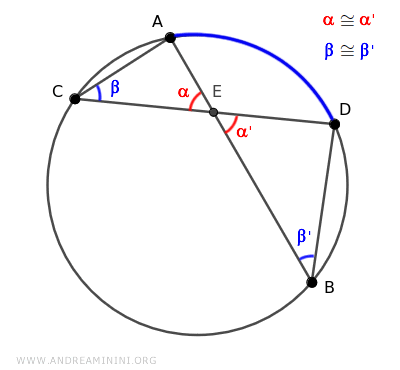
Di conseguenza, per il primo criterio di similitudine dei triangoli, i triangoli ACE e BDE sono simili perché hanno due angoli congruenti α≅α' e β≅β'.
Essendo simili, i triangoli ACE e BDE hanno i lati omologhi proporzionali.
$$ \overline{AC} : \overline{BD} = \overline{AE} : \overline{DE} = \overline{CE} : \overline{EB} $$
Nota. Per trovare i lati omologhi basta vedere qual è il lato opposto agli angoli congruenti nei due triangoli. Ad esempio, sapendo che α≅α' sono congruenti, il lato opposto all'angolo α nel triangolo ACE è il lato AC, mentre il lato opposto all'angolo α' nel triangolo BDE è il lato BD. Quindi, AC e BD sono due lati omologhi dei due triangoli.
La proporzione che ho appena trovato conferma il teorema iniziale.
$$ \overline{AE} : \overline{DE} = \overline{CE} : \overline{EB} $$
I segmenti di una corda DE e CE sono i medi mentre i segmenti dell'altra corda AE e EB sono gli estremi di una proporzione.

E così via.
