La potenza di un punto rispetto a una circonferenza

La potenza di un punto P(x;y) rispetto a una circonferenza \( (x - a)^2 + (y - b)^2 = r^2 \) è la differenza tra il quadrato della distanza del punto dal centro C(a,b) della circonferenza meno il quadrato del raggio. $$ \pi(P)  = d^2 - r^2 $$

Sapendo che la distanda d tra due punti si ottiene tramite la formula

$$ d = \sqrt{((x - a)^2 + (y - b)^2  } $$

La potenza del punto rispetto alla circonferenza si calcola tramite questa formula

$$ \pi(P)  = (x - a)^2 + (y - b)^2 - r^2 $$

Questa grandezza misura la distanza "relativa" del punto dalla circonferenza.

Nota. Non misura la distanza euclidea del punto dalla circonferenza perché considera anche il raggio della circonferenza,

Il segno della potenza individua la posizione del punto P rispetto alla circonferenza.

• Se \(\pi(P) > 0\), il punto sta fuori dalla circonferenza.
• Se \(\pi(P) = 0\), il punto sta sulla circonferenza.
• Se \(\pi(P) < 0\), il punto sta dentro la circonferenza.

Un esempio pratico

Considero un punto P(6,3) e una circonferenza con centro C(3,3) e raggio r=2.

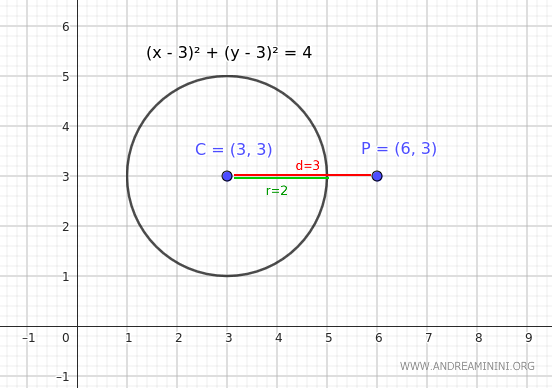
La distanza del punto P dal centro C della circonferenza è facilmente calcolabile ed è uguale a 3.

$$ d = \sqrt{((6 - 3)^2 + (3 - 3)^2  } = \sqrt{3^2} $$

$$ d = 3 $$

Quindi, la potenza del punto P rispetto alla circonferenza è uguale alla differenza tra i quadrati della distanza e del raggio

$$ \pi(P) = d^2 - r^2 $$

$$ \pi(P) = 3^2 - 2^2 $$

$$ \pi(P) = 9 - 4 $$

$$ \pi(P) = 5 $$

In questo caso la potenza del punto è uguale a 5.

Esempio 2

Considero un punto P(7,6) e sempre la stessa circonferenza dell'esempio precedente, quella con centro C(3,3) e raggio r=2.

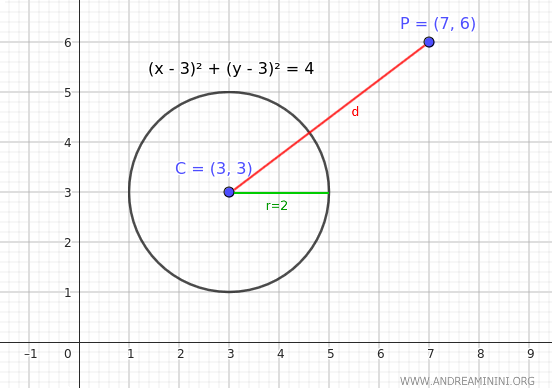
In questo caso il punto è più lontano rispetto all'esempio precedente ma il raggio della circonferenza è uguale.

Calcolo la distanza tra il centro della circonferenza e il punto P

$$ d = \sqrt{((x - a)^2 + (y - b)^2  } $$

$$ d = \sqrt{((7 - 3)^2 + (6 - 3)^2  } $$

$$ d = \sqrt{(4^2 + 3^2  } $$

$$ d = \sqrt{(16 + 9  } $$

$$ d = \sqrt{(25  } $$

$$ d = 5 $$

Sapendo che il raggio della circonferenza è r=2, calcolo la potenza del punto P rispetto alla circonferenza.

$$ \pi(P) = d^2 - r^2 $$

$$ \pi(P) = 5^2 - 2^2 $$

$$ \pi(P) = 25 - 4 $$

$$ \pi(P) = 21 $$

La potenza del punto rispetto alla circonferenza è uguale a 21.

Osservazioni

Alcune note a margine sulla potenza di un punto rispetto a una circonferenza

• Un punto P con la stessa potenza rispetto a due circonferenze si trova sull'asse radicale
  Se considero due circonferenze con centri \(C_1\) e \(C_2\) e raggi \(r_1\) e \(r_2\), un punto \(P\) che ha la stessa potenza rispetto a entrambe le circonferenze soddisfa l'equazione: \[ (x - x_1)^2 + (y - y_1)^2 - r_1^2 = (x - x_2)^2 + (y - y_2)^2 - r_2^2 \] Questo punto si trova su una retta detta "asse radicale", si tratta di una linea dove le potenze rispetto alle due circonferenze sono uguali, indipendentemente dalle distanze fisiche.
• Un punto P che si trova sull'asse radicale è più vicino al centro della circonferenza con raggio inferiore.
  Questo si deduce facilmente guardando l'equazione \[ (x - x_1)^2 + (y - y_1)^2 - r_1^2 = (x - x_2)^2 + (y - y_2)^2 - r_2^2 \] Se uno dei due lati ha raggio inferiore anche la distanza tra il punto e il centro della circonferenza deve essere inferiore, per mantenere l'uguaglianza con l'altro lato dell'equazione ovvero la stessa potenza dell'altra circonferenza. $$ \pi_1(P) = \pi_2(P) $$ $$ (x - x_1)^2 + (y - y_1)^2 - r_1^2 = (x - x_2)^2 + (y - y_2)^2 - r_2^2  $$ $$ \pi_1(P) = \pi_2(P) $$ $$ (x - x_1)^2 + (y - y_1)^2 - [r_1^2 - \Delta r + \Delta r] = (x - x_2)^2 + (y - y_2)^2 - r_2^2  $$ $$ (x - x_1)^2 + (y - y_1)^2 - \Delta r - [r_1^2 - \Delta r ] = (x - x_2)^2 + (y - y_2)^2 - r_2^2  $$ $$ [ (x - x_1)^2 + (y - y_1)^2 - \Delta r ] - [r_1^2 - \Delta r ] = (x - x_2)^2 + (y - y_2)^2 - r_2^2  $$

  Esempio. Considero una circonferenza con centro in C(3,3) e raggio r=2 e un punto P(6,3). Ho già calcolato la potenza di questo punto rispetto alla circonferenza ed è pari a $ \pi(P)=5 $ Per trovare un altra circonferenza con la stessa potenza ma raggio r=1, posso usare la formula della potenza $$ \pi(P) = d^2 - r^2 $$ In questo caso conosco la potenza del punto P rispetto alla prima circonferenza $ \pi = 5 $ e il raggio $ r=1 $ della nuova circonferenza $$ 5 = d^2 - 1^2 $$ Quindi, la nuova circonferenza si deve trovare a una distanza pari a rad(6)=2.4495 dal punto P $$ d^2 = 5+1 $$ $$ d = \sqrt{6} $$ In conclusione, la nuova circonferenza ha un raggio inferiore e per avere la stessa potenza deve avere anche una distanza inferiore.
  
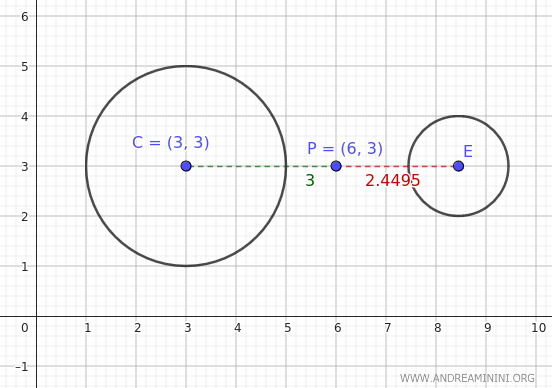
  Come verifica finale calcolo la potenza del punto P(6,3) rispetto alla nuova circonferenza con raggio r=1 che dista d=√6  dal punto P quindi ha il centro in E(6+√6,3). $$ \pi(P) = d^2 - r^2 $$ $$ \pi(P) = (\sqrt{6})^2 - 1^2 $$ $$ \pi(P) = 6 - 1 $$ $$ \pi(P) = 5 $$ Il punto P ha la stessa potenza π(P)=5 anche nei confronti della nuova circonferenza.

E così via.