Il teorema della proporzionalità tra secante e tangente
Se da un punto esterno P a una circonferenza traccio una tangente e una secante, il segmento di tangente è medio proporzionale tra i due segmenti di secante che partono da P e hanno per estremi i punti di intersezione con la circonferenza.
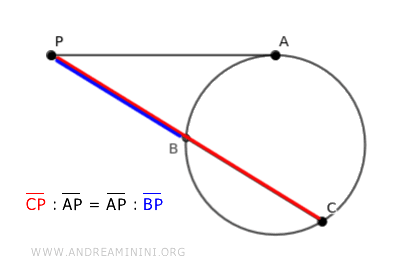
Un esempio pratico
Prendo come esempio questa situazione.
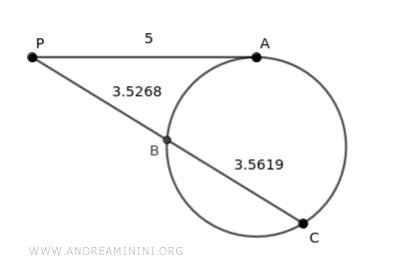
Il segmento di tangente AP misura 5.
$$ \overline{AP} = 5 $$
Il segmento di secante CP è pari alla somma dei segmenti BP+BC
$$ \overline{CP} = \overline{BP} + \overline{BC} $$
$$ \overline{CP} = 3.5268+3.5619= 7.09 $$
Secondo il teorema il segmento di secante CP sta al segmento di tangente AP come AP sta a BP.
$$ \overline{CP} : \overline{AP} = \overline{AP} : \overline{BP} $$
$$ 7.09 : 5 = 5 : 3.5268 $$
$$ 1.41 = 1.41 $$
La proporzione è confermata e il segmento di tangente è il medio proporzionale.
Nota. Ho approssimato i quozienti a due cifre decimali perché la misura dei segmenti fatta con geogebra è approssimata a quattro cifre decimali.
La dimostrazione
Considero una circonferenza e un punto P esterno.
Traccio una tangente e una secante.
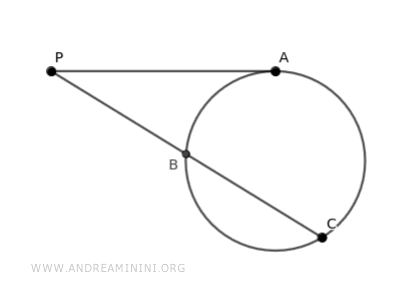
La tangente tocca la circonferenza nel punto A, mentre la secante interseca la circonferenza nei punti B e C.
Traccio altri due segmenti AB e AC.
In questo modo ottengo due triangoli ABP e ACP.
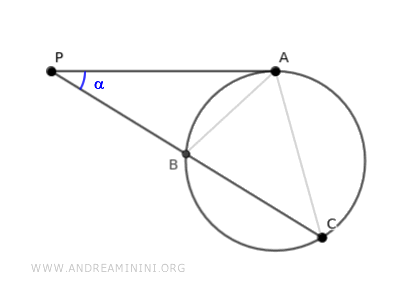
I due triangoli ABP e ACP hanno l'angolo α coincidente.
Inoltre, hanno anche gli angoli β≅γ congruenti perché sono angoli alla circonferenza che insistono sullo stesso arco di circonferenza AB.
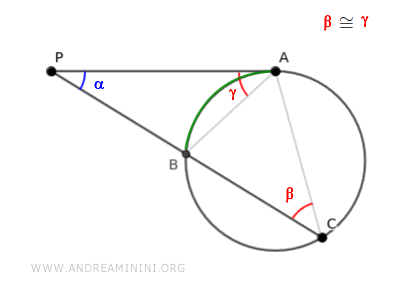
Quindi, per il primo criterio di similitudine dei triangoli, i triangoli ABP e ACP sono simili, in quanto hanno un angolo coincidente α e un angolo congruente e β≅γ
$$ ABP \approx ACP $$
Essendo triangoli simili, hanno i lati omologhi proporzionali.
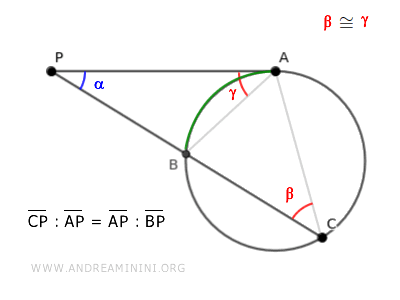
$$ \overline{AB} : \overline{AC} = \overline{BP} : \overline{AP} = \overline{AP} : \overline{CP} $$
Questo dimostra il teorema.
$$ \overline{BP} : \overline{AP} = \overline{AP} : \overline{CP} $$
Il segmento di tangente AP è il medio proporzionale tra i segmenti della secante.
E così via.
