Equazione della circonferenza in forma polare
L'equazione della circonferenza in forma polare è $$ r^2+r_c^2-2 \cdot r \cdot r_c \cos (\alpha - \alpha_c) - R^2 = 0 $$ Dove R è il raggio della circonferenza, rc e r sono i segmenti che congiungono il polo (origine) con il centro C e un punto qualsiasi P della circonferenza.
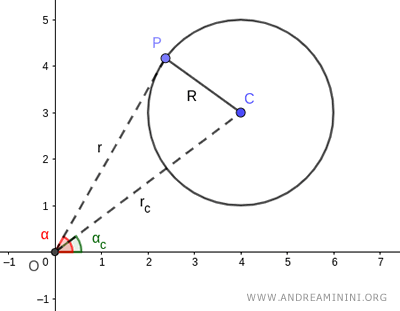
Variando le coordinate polari (α,r) ottengo tutti i punti della circonferenza.
Dove l'angolo α e la lunghezza del segmento r sono le variabili.
La dimostrazione
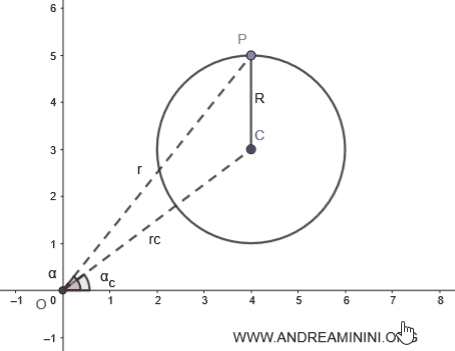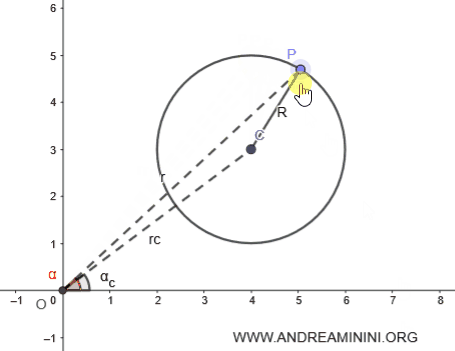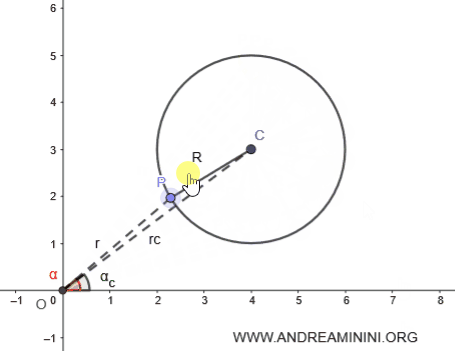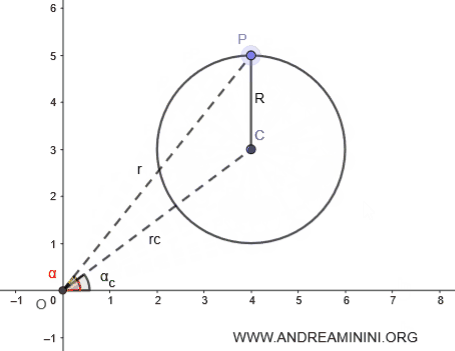
Considero una circonferenza qualsiasi sul piano.
La circonferenza ha un raggio pari a R=2.
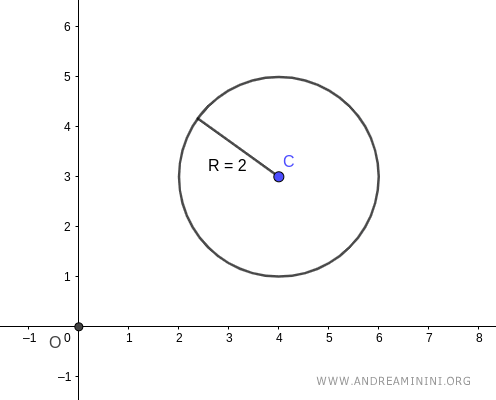
Il centro della circonferenza C si trova alle coordinate polari (αc,rc).
$$ C: (\alpha_c, r_c) = ( 36.87°, 5) $$
Dove l'angolo αc=36.87° e il segmento rc=5
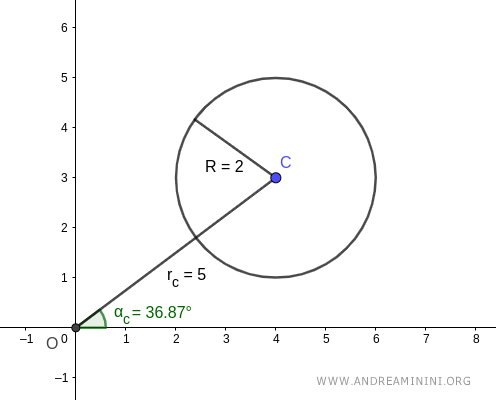
Prendo un punto qualsiasi P della circonferenza.
$$ P : (\alpha, r) = ( 60.27°, 4.8) $$
Il punto P ha le coordinate polari α=60.27° e r=4.8
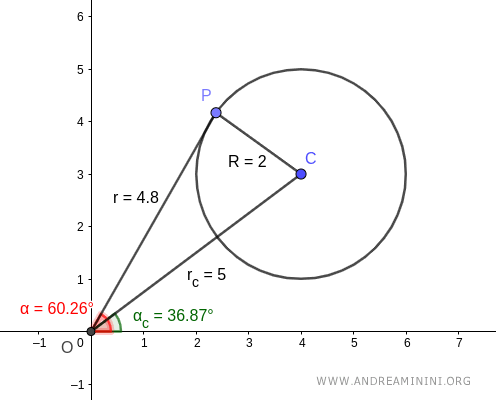
Il raggio R e i segmenti OP e OC formano un triangolo OPC.
Applico il teorema del coseno al triangolo OPC
$$ \overline{PC}^2 = \overline{OP}^2 + \overline{OC}^2 - 2 \cdot \overline{OP} \cdot \overline{OC} \cdot \cos ( \alpha - \alpha_c ) $$
Sapendo che i lati del triangolo sono PC=R, OC=rc, OP=r
$$ R^2 = r^2 + r_c^2 - 2 \cdot r \cdot r_c \cdot \cos ( \alpha - \alpha_c ) $$
Sposto tutti i termini da una sola parte
$$ r^2 + r_c^2 - 2 \cdot r \cdot r_c \cdot \cos ( \alpha - \alpha_c ) - R^2 = 0 $$
Il risultato finale è l'equazione della circonferenza in forma polare che volevo dimostrare.
Verifica. Sostituendo i valori delle coordinate polari α=60.27°, αc=36.87°, r=4.8, rc=5 e del raggio R=2 l'equazione è soddisfatta $$ R^2 = r^2 + r_c^2 - 2 \cdot r \cdot r_c \cdot \cos ( \alpha - \alpha_c ) $$ $$ 5^2 = 4.8^2 + 5^2 - 2 \cdot 4.8 \cdot 5 \cdot \cos ( 60.27° - 36.87° ) $$ $$ 25 = 23.04 + 25 - 2 \cdot 24 \cdot \cos ( 23.4° ) $$ $$ 25 = 48 - 44 $$ $$ 25 = 25 $$ L'identità è rispettata.
Un esempio pratico
E' sempre possibile convertire l'equazione della circonferenza dalla forma polare a quella cartesiana, e viceversa.
Esempio 1
In questo esempio considero una circonferenza definita da un'equazione in forma polare
$$ r^2 - 3r \cos \alpha + 2 = 0 $$
Per trasformarla in forma cartesiana, basta ricordare che il raggio della circonferenza si ottiene utilizzando il teorema di Pitagora sulle coordinate (x;y)
$$ r = \sqrt{x^2+y^2} $$
Inoltre, le coordinate x e y sono
$$ x = r \cos \alpha $$
$$ y = r \sin \alpha $$
Per prima cosa sostituisco $ x = r \cos \alpha $ nell'equazione
$$ r^2 - 3r \cos \alpha + 2 = 0 $$
$$ r^2 - 3x + 2 = 0 $$
Poi sostituisco $ r= \sqrt{x^2+y^2} $ nell'equazione in $ r^2 $
$$ (\sqrt{x^2+y^2})^2 - 3x + 2 = 0 $$
$$ x^2+y^2 - 3x + 2 = 0 $$
In questo modo ho ottenuto l'equazione in forma cartesiana.
Esempio 2
Per convertire l'equazione della circonferenza dalla forma cartesiana a quella polare, seguo il processo inverso.
Ad esempio, considero l'equazione
$$ x^2+y^2 - 3x + 2 = 0 $$
Sostituisco $ x = r \cos \alpha $
$$ x^2+y^2 - 3 r \cos \alpha + 2 = 0 $$
Poi considerando $ r = \sqrt{x^2+y^2} $ sostituisco $ r^2 = x^2+y^2 $
$$ r^2 - 3 r \cos \alpha + 2 = 0 $$
In questo modo ho ottenuto la forma polare dell'equazione.
E così via.
