Incentro
L'incentro di un triangolo è il punto di intersezione (I) delle bisettrici dei suoi angoli interni ed è il centro del cerchio inscritto nel triangolo (incerchio).
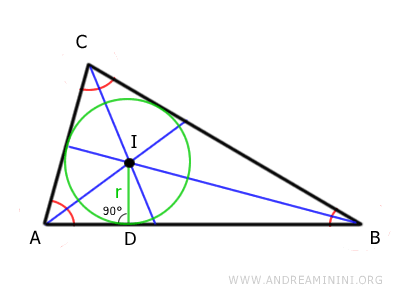
La principale caratteristica dell'incentro (I) è di essere equidistante da tutti e tre i lati del triangolo.
Questa distanza (ID) è il raggio del cerchio inscritto nel triangolo detto incerchio.
La circonferenza inscritta dell'incerchio ha la caratteristica di essere tangente ai tre lati del triangolo, cioé li tocca senza attraversarli.
Il raggio del cerchio inscritto nel triangolo è anche detto inraggio.
Come si trova l'incentro?
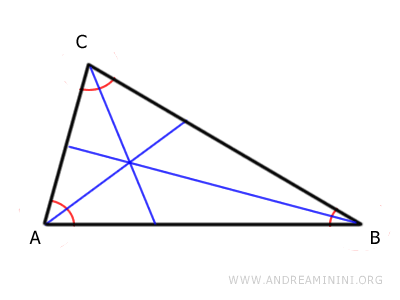
Per determinare l'incentro traccio la bisettrice di ogni angolo interno del triangolo.
La bisettrice è la semiretta che divide in due parti uguali ciascun angolo.
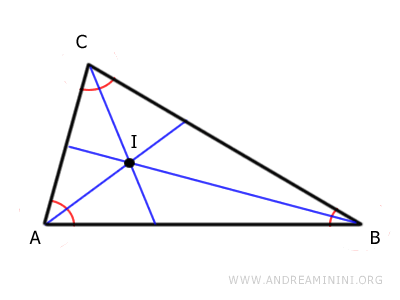
Il punto di intersezione (I) delle bisettrici è un punto interno al triangolo detto incentro.
Infine, traccio un segmento (ID) perpendicolare a un lato del triangolo, a mia scelta, che ha per estremo l'incentro (I).
In questo caso scelgo il lato AB.
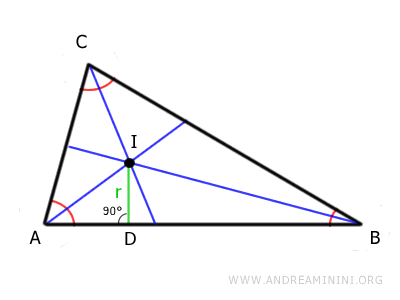
Questo è detto inraggio ed è il raggio del cerchio inscritto nel triangolo ( detto incerchio ).
Il cerchio inscritto ha per centro l'incentro.

Una delle caratteristiche dell'incerchio è di essere tangente a tutti e tre i lati del triangolo.
La dimostrazione
Considero un generico triangolo ABC.
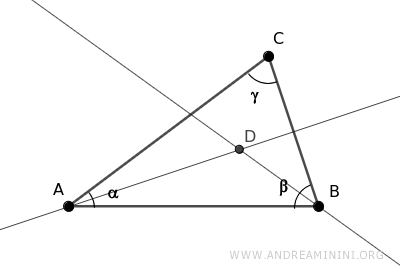
Traccio le bisettrici degli angoli α e β.
Sapendo che la somma degli angoli di un triangolo è sempre 180° (angolo piatto)
$$ \alpha + \beta + \gamma = 180° $$
deduco che la somma degli angoli alfa e beta è minore di 180°.
$$ \alpha + \beta < 180° $$
Pertanto, anche la somma della metà degli angoli alfa e beta è minore di 180° e questo vuol dire che le due bisettrici degli angoli α e β si incontrano sicuramente in un punto di intersezione D.

Traccio le perpendicolari ai lati del triangolo che passano per il punto D.
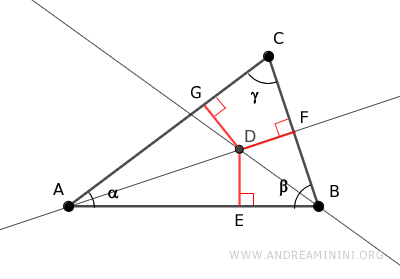
I segmenti DE≅DF sono congruenti perché il punto D appartiene alla bisettrice dell'angolo beta, quindi è equidistante dai lati dell'angolo beta.
$$ \overline{DE} \cong \overline{DF} $$
Anche i segmenti DE≅DG sono congruenti, perché il punto D appartiene alla bisettrice dell'angolo alfa, quindi è equidistante dai lati dell'angolo alfa.
$$ \overline{DE} \cong \overline{DG} $$
Per la proprietà transitiva, se DE≅DF e DE≅DG allora anche i segmenti DF≅DG sono congruenti.
$$ \overline{DF} \cong \overline{DG} $$
Questo vuol dire che il punto di intersezione D è equidistante dai lati dell'angolo γ , quindi appartiene alla bisettrice dell'angolo γ.
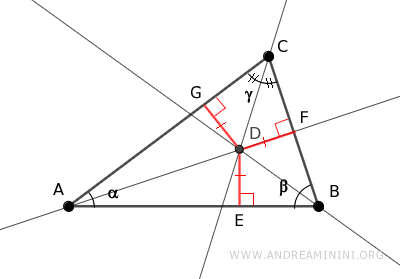
Questo dimostra che il punto di intersezione D appartiene a tutte le bisettrici degli angoli del triangolo.
Osservazioni
Alcune osservazioni e proprietà dell'incentro.
- Ogni triangolo è circoscrivibile a una circonferenza che ha come centro l'incentro.
- L'incentro è equidistante da tutti e tre i lati del triangolo. Questa distanza è il raggio del cerchio inscritto.
- La posizione dell'incentro varia a seconda della forma del triangolo. Ad esempio, in un triangolo equilatero, l'incentro coincide con il baricentro, il circocentro e l'ortocentro.
- L'incentro di un triangolo separa ogni bisettrice in due segmenti, i quali hanno un rapporto proporzionale ai lati del vertice rispetto alle parti delimitate da essa sul lato opposto.
- La circonferenza inscritta (incerchio) che ha per centro l'incentro è tangente ai lati del triangolo.
E così via.
